4. Условная и полная вероятности

4. Условная и полная вероятности

Условная вероятность – такая вероятность события А, которая вычислена при предположении, что событие Д произошло: при этом события А и В являются зависимыми, они обозначаются как Р(А /В) или Р(А)В.

Совместное (одновременное или последовательное) появление нескольких независимых событий А, В, С, Fназывается сложным событием. Вероятность сложного события определяется путем умножения вероятностей составляющих его событий.

Р (АиВиСи…иF)= Р(А) ? Р(В)_А ? Р (С_АВ) ?… ? Р(F)_АВС.

В случае независимости событий (8) выглядит следующим образом.

Р (АиВиСи…иF)= Р (А) ? Р (В) ? Р (С) ? … ? Р (f).

Формула, которую привели выше, справедлива, если события А или В или С несовместимы. В случае их совместимости формула выглядит следующим образом:

Р(А ? В ? С)=Р(А) + Р(В) + Р(С) – Р(АиВиС).

Р (АиВиС)= Р (А) ? Р(В) ? Р (С)

С учетом этого получим

Р (А ? В ? С)=Р (А) + Р (В) + Р (С) – Р (А) ? Р (В) ? Р (С).

Теперь, после некоторого ознакомления с арифметическими операциями над вероятностями, можно привести формулу полной вероятности

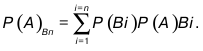
В формуле предполагается, что событие А может произойти только с одним из n несовместимых событий B₁….,B_n, то есть группа событий А и B₁, или А и B₂ и т. д. Любая группа из этого ряда равносильна появлению события А.

Пример 2. Пусть события D, Е, F независимые. Какова будет вероятность событий трех извлечений подряд небракованных деталей при условии, что выборка повторная.

Решение. При данном условии после извлечения каждый раз бракованной детали, а больше одной детали нельзя извлечь, количество бракованных деталей с каждым разом уменьшается на единицу. В третий раз будет извлечена последняя бракованная деталь.

Данный текст является ознакомительным фрагментом.