Кодирование

Концепция дискретного представления информации на основе знаков некоторого конечного алфавита, как отображение событий, соответствующих определенным квантам (минимальным порциям) информации, подводит к возможности выработки меры оценки количества информации. Существуют формальные приемы отображения знаков одного алфавита с помощью знаков другого. Это обусловлено тем, что алфавиты могут быть представлены в виде конечных счетных множеств, элементы которых можно занумеровать числами натурального ряда. На основании этого взаимное отображение алфавитов достигается на основе теоретико-множественных процедур с элементами алфавитных множеств и их подмножествами. Именно числ овая форма представления информации нашла глубокое применение в вычисл ительной технике, само название которой подчеркивает эту форму представления информации. Нам рассказывали, что до наступления эры компьютеризации классные китайские телеграфистки «на ходу» переводили иероглифы в цифровой код, лишь изредка сверяясь с таблицами перевода.

Необходимо отметить, что взаимоотображение алфавитов на основе формальных теоретико-множественных процедур не учитывает содержательной (семантической) значимости (если она имеется) алфавитных знаков. Но вместе с тем, формализация на основе теоретико-множественного представления информации позволяет выработать единый подход к оценке количества информации при знаковой форме отображения событий, соответствующих определенным квантам (минимальным порциям) информации.

В основе всей теории информации лежит открытие, сделанное Р.Хартли в 1928 году, и состоящее в том, что информация допускает количественную оценку. Подход Р.Хартли базируется на фундаментальных теоретико-множественных, по существу комбинаторных, основаниях, а также некоторых интуитивно очевидных предположениях. Если считать, что существует множество элементов и осуществляется выбор одного из них, то этим самым сообщается или генерируется определенное количество информации. Эта информация состоит в том, что если до выбора не было известно, какой элемент будет выбран, то после выбора это становится известным.

Если множество элементов, из которых осуществляется выбор, состоит из одного единственного элемента, то его выбор предопределен, т.е. никакой неопределенности выбора нет. Это означает нулевое количество информации. Если множество состоит из двух элементов, то неопределенность выбора существует, и ее значение минимально. В этом случае минимально и количество информации, после того как совершен выбор одного из элементов. Это количество информации принято за единицу измерения и называется бит[21]. Чем больше элементов содержит множество, тем больше неопределенность выбора, т.е. тем больше заключено в нем информации. На основании этого Р.Хартли предложена мера оценки количества информации (H), получаемой при реализации (выборе) одного из N состояний: H=log₂N. Эта мера является адекватной в предположении, что равновероятен выбор любого элемента из множества состояний.

В середине ХХ столетия К.Шеннон дал более широкую интерпретацию количественной оценки информации в сравнении с тезисами Р.Хартли. Подход К.Шеннона основывается на теоретико-вероятностном подходе. Это связано с тем, что исторически теория информации К.Шеннона выросла из потребностей теории связи, имеющей дело со статистическими характеристиками передаваемых сообщений по каналам связи. К.Шеннон обобщает представление Р.Хартли, учитывая, что различные события в общем случае не равновероятны.

В литературе часто утверждается, о неправомерности применения формулы К.Шеннона для оценки количества семантической информации. Отечественный ученый В. Г.Толстов в своих работах показал, что количество информации, определяемое по формуле К.Шеннона, является интегральной оценкой объема кванта полной и точной информации, описывающей сообщение x на уровне его представления категориальной моделью M_x. По мнению В. Г.Толстова предлагаемый в его теории квантовой информатики подход к оценке объемов информации позволяет утверждать о возможности использования формулы К.Шеннона для оценки количества семантической информации и при этом достаточно точно установить границы ее применимости и для этого случая. Такая декларация имеет существенное феноменологическое значение с точки зрения преодоления часто обсуждаемых противоречий в количественной оценке ситуационного (событийно-вероятностного) и семантического представления информации.

Чрезвычайно важным и принципиальным является то обстоятельство, что для построения меры Р.Хартли используется лишь понятие многообразия, которое накладывает на элементы исходного множества лишь одно условие (ограничение): должна существовать возможность отличать эти элементы один от другого. В теории К.Шеннона существенным образом используется статистика и очевидно, что мера К.Шеннона асимптотически переходит в меру Р.Хартли при условии, что вероятности всех событий (состояний) равны.

Приведенные меры оценки количества информации не несут в себе представления и способов идентификации идеоморфности[22]знаковой формы отображения событий, соответствующих определенным квантам (минимальным порциям) информации. С этой точки зрения суть процедур кодирования заключается в группировании алфавитных знаков в кодовое слово так, чтобы эти слова соответствовали идиоморфизмам данной системы. При передаче по телеграфу, например, идиоморфизмами являются буквы, цифры, знаки препинания и знак пробела, а в естественных языках идеоморфизмами являются понятия, обозначаемые словами. Это качественное преобразование можно выделить в самостоятельный феноменологический уровень представления информации.

Формализация этого явления при передаче, хранении и обработке информации обычно связывается с операцией отождествления символов или групп символов одного кода с символами или группами символов другого кода. Если задано множество элементов сообщений (идиоморфизмов) B= {b_i}, где i =1,…,N (N – мощность множества B), и присутствует некоторый алфавит A с символами a_k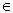A, где k =1,…,m и m – размерность алфавита, то К – множество конечных последовательностей символов a_k, называемых словами в данном алфавите А, называется кодом К, если множество К поставлено во взаимно однозначное соответствие с множеством В. Слова, входящие в множество К, называются кодовыми словами (кодовыми комбинациями), а число символов в кодовых словах называется длинной кодовых слов; m – размерность алфавита А, называется основанием кода К.

По форме, кодирование – это структуризация последовательности алфавитных знаков с целью передачи информации в пространстве или во времени или для ее преобразования. Наряду с алфавитом процедуры кодирования и соответствующие им при приеме (чтении) информации процедуры декодирования должны учитывать направленность кода. Очевидно, что в самом коде сведения о его направленности отсутствуют, и необходимы дополнительные системные механизмы (соглашения), обеспечивающие восприятие направленности кода.

В технических системах направленность кода регламентируются некоторыми стандартами и рекомендациями, например, государственных и международных организаций. На их основе обеспечивается возможность согласованного функционирования всей инфраструктуры связи Земного шара. Академик Латвийской академии наук Э. А.Якубайтис, описывая, например, протоколы вычислительных сетей, подчеркивает: «Передача физических блоков информации осуществляется так, что биты принимаются в конце физического соединения в том же порядке, в каком они были переданы в начале соединения».

В компьютерах размер ячейки основной памяти обычно принимается равным 8 двоичным разрядам – байту. Для хранения больших чисел используются 2, 4 или 8 байтов, размещаемых в ячейках с последовательными адресами. В этом случае за адрес числа часто принимается адрес его младшего байта. Такой прием называют адресацией по младшему байту (little endian addressing). Он характерен, например, для микропроцессоров фирмы Intel, США, а также был характерен для ЭВМ фирмы DEC (Digital Equipment Corporation), США. Возможен и противоположный подход – по меньшему из адресов располагается старший байт. Этот способ известен как адресация по старшему байту (big endian addressing), характерный, например, для микропроцессоров фирмы Motorola и универсальных ЭВМ фирмы IBM. В большинстве компьютеров предусмотрены специальные инструкции для перехода от одного способа к другому.

В биологических системах последовательность считывания генетической информации регулируется механизмом хиральности.[23]Английский физик лорд Кельвин (W.Thomson), определивший понятие «хиральность» писал в 1893 г.: «Я называю геометрическую фигуру хиральной, если ее отражение в зеркале не совпадает с нею при наложении (подобно рукам человека)». Молекула называется хиральной, если ее пространственная конфигурация не инвариантна относительно зеркального отражения. Подавляющее большинство биоорганических соединений живой природы – хиральны. В частности: аминокислоты, сахара и нуклеотиды, участвующие в жизненных процессах живых организмов. Хиральная молекула имеет две зеркально антиподные пространственные конфигурации – левый (L) и правый (D) энантиомеры. Процесс считывания информации, как он сегодня представляется биологам, чрезвычайно усложнился бы, если блоки, из которых построены считываемые и считывающие молекулы на основе нуклеиновых кислот и белков, были представлены рацемическими (хирально неупорядоченными) смесями своих мономеров.

Направленность кода также как и алфавит не определяются непосредственно типом, содержанием или какими-либо другими показателями информации. Их выбор определяется системными (или надсистемными) соглашениями и/или традициями, обычно обусловленными возможностями материальной (hardware) реализации необходимых способов обработки и передачи информации.

Эффективность кодирования существенным образом зависит от того, какое количество уникальных представлений возможно при фиксированных значениях мощности алфавита и длине кода. Естественно, что увеличение количества кодируемых комбинаций в заданных условиях повышает эффективность процедуры кодирования. Максимальное значение эффективности кодирования может быть достигнуто, когда обеспечивается различие любых комбинаций размещения символов алфавита с повторениями. Это эквивалентно позиционным системам счисления. Однако в реальных условиях достижение такого многообразия значений обычно не происходит. Это объясняется тем, что при передаче информации возможны искажения. Определить наличие ошибки в переданном коде можно только за счет его избыточности. Существуют различные способы избыточного кодирования, которые позволяют в ряде случаев не только идентифицировать наличие ошибки при передаче, но и исправить некоторые из них. Такие коды называются корректирующими.

Феноменологически, в отличие от знаков алфавита и принятого для них направления кодирования, сам процесс кодирования значительно глубже связан уже с содержательной стороной информации (например, мощность множества отображаемых идиоморфизмов). Вместе с тем процессы кодирования более глубоко охватывают и подходы к материальной реализации информационных систем, учитывая возможные воздействия различных факторов, приводящих к искажению информации.