Парадоксы теории множеств
Парадоксы теории множеств
«Никто не может изгнать нас из рая, созданного нам Кантором!» — заявил Давид Гильберт по поводу теории множеств Георга Кантора. Таково было чувство восторга от новой «игрушки» у математиков того времени. В 1873 году Кантор ввел понятие множества. Первоначально новая теория помогла решить ряд проблем. Однако очень скоро в ней обнаружились противоречия.
Первое противоречие возникло благодаря введению и анализу самого большого множества из всех: множества всех множеств. Простейший вопрос «Существует ли множество всех множеств?» тут же приводит к парадоксу. Для этого надо напомнить, что в теории множеств разрешима процедура включения одного множества в состав другого или «взятие множества от множества». (Это вам ничего не напоминает? Правильно — вездесущую рекурсию!)
Можно включать какие угодно множества в состав одного — их объединяющего, до тех пор пока все множества не исчерпаются. Тогда мы получим сверхмножество, которое включает в себя все остальные множества. Все! Но не все! Само сверхмножество (множество всех множеств) оказалось не включённым! Ведь его вначале не было, а теперь оно появилось. Ну что же, включим теперь и его. Но тогда появляется новое сверхмножество, которого только что ещё не было. Тогда и его включим, и так до бесконечности! То есть множество всех множеств и существует, и не существует одновременно!
Причиной парадокса является возможность быть множеству элементом самого себя. Можно конечно ограничить эту возможность, но тогда исчезнут многие очень полезные возможности теории множеств. Лучше локализовать проблему, и для этого разделить все множества на два типа, те, которые содержат себя в качестве своего элемента, и те, которые не содержат..
В 1901 году Бертран Рассел в письме коллеге изложил мысль, которая в популярной форме известна как «Парадокс брадобрея»: «В одной военной части был брадобрей. Ему было разрешено под угрозой смертной казни брить только тех военнослужащих, которые не бреются сами. Но вот беда — сам брадобрей тоже был на службе. Мог ли он в таком случае побриться сам?»
Если он себя побреет, то окажется тем, кого ему брить категорически запрещено, а если не побреет, то окажется среди тех, кого брить ему можно!
Словом, в теории множеств выявилось много противоречий[92], а на их устранение потратили огромное количество усилий. Собственно, как и в случае с математическим анализом, который первоначально был противоречив и только трудами титанов — Коши, Вейерштрасс, Гейне — приведён в образцовое состояние. В условно образцовое. Ибо все противоречия математического анализа были упрятаны в его определения, совмещающие в себе невозможное. Достаточно вспомнить бесконечно малые и бесконечно большие величины, которые «куда-то стремятся, но никогда своего предела не достигают». При этом само стремление к пределу происходит вне времени, что невозможно само по себе — в природе такое не наблюдается.
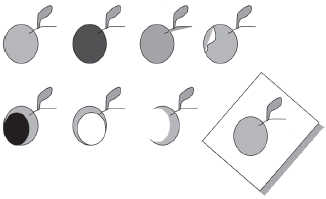
ВОПРОС № 98
Сколько яблок на рисунке?[93]
Данный текст является ознакомительным фрагментом.