1.4.2. Обнаружение ЦВЗ с нулевым знанием

1.4.2. Обнаружение ЦВЗ с нулевым знанием

Робастные ЦВЗ могут применяться в различных приложениях, соответственно, и требования к ним могут предъявляться различные. Можно выделить следующие категории требований к робастным ЦВЗ:

— ЦВЗ обнаруживается всеми желающими. В этом случае он служит для уведомления о собственнике защищаемого контента и для предотвращения непреднамеренного нарушения прав собственника.

— ЦВЗ обнаруживается, по крайней мере, одной стороной. В этом случае его использование связано с поиском нелегально распространяемых копий, например, в сети Интернет.

— ЦВЗ крайне трудно модифицировать или извлечь из контента. В этом случае ЦВЗ служит для аутентификации.

Одновременное выполнение вышеприведенных требований невозможно, так как они являются противоречивыми. Поэтому, в различных приложениях используются как системы ЦВЗ с секретным, так и с общедоступным ключом. Системы с общедоступным ключом находят гораздо большее применение, так как они могут быть использованы как для обнаружения, так и для предотвращения несанкционированного использования контента. Для того, чтобы поисковая система обнаружила ЦВЗ с секретным ключом, ей необходимо проверить каждое изображение на наличие в нем каждого из возможных ЦВЗ, что является вычислительно трудоемкой задачей. В случае же общедоступного ЦВЗ алгоритм обнаружения единственный. Однако, общедоступные ЦВЗ обладают серьезным недостатком: так как их местоположение известно, то их можно без труда извлечь из защищаемого изображения.

Создается впечатление, что ЦВЗ с общедоступным ключом не могут быть робастными. Однако, является ли таковым ЦВЗ с секретным ключом? Да, его местоположение неизвестно, но лишь до тех пор, пока он не «вступает в действие». Как только ЦВЗ начинает выполнять свои функции по защите контента, у атакующего появляется все больше информации о нем, то есть ЦВЗ становится все более «открытым». В главе 2 представлен ряд атак, связанных с выявлением поведения детектора при незначительных модификациях изображения. Таким образом, сама природа ЦВЗ такова, что их в любом случае можно считать общедоступными, несмотря на наличие секретного ключа.

В работе [14] представлена система ЦВЗ, в которой этапы аутентификации и обнаружения разделены. Это делает возможным создание ЦВЗ, который легко обнаруживается, но трудно удаляется. Эта система строится на основе доказательства с нулевым знанием [11].

Представим себе следующую ситуацию. Алиса обладает некоторой информацией и хочет доказать этот факт Бобу. При этом доказательство должно быть косвенным, то есть Боб не должен получить каких-либо новых знаний об этой информации. Такое доказательство и называется доказательством с нулевым знанием. Оно принимает форму интерактивного протокола. Боб задает Алисе ряд вопросов. Если Алиса действительно владеет некоторой информацией, то она ответит на все вопросы правильно; если же она мошенничает, то вероятность правильного угадывания мала и уменьшается с увеличением количества вопросов.

В целом базовый протокол с нулевым знанием строится следующим образом:

1. Алисе известна некоторая информация, являющаяся решением некоторой трудной проблемы. Она использует эту информацию и случайное число для превращения этой трудной проблемы в другую, изоморфную первой и получает ее решение.

2. Боб просит Алису либо доказать, что старая и новая проблемы изоморфны, либо открыть решение новой проблемы и доказать, что оно является таковым. Алиса выполняет просьбу Боба.

3. Этапы 1 и 2 повторяются n раз.

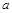В качестве трудной проблемы выбирается обычно вычисление по однонаправленной функции. Одной из наиболее известных однонаправленных функций является дискретный логарифм. Рассмотрим построение протокола с нулевым знанием на основе дискретного логарифма. При этом общеизвестными являются: большое простое число и порождающий элемент . Алиса выбирает некоторое число 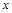и публикует 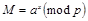. Так как определение 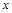на основе знания M есть вычислительно трудная задача, то знание Алисой 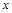подтверждает ее идентичность.

Протокол строится следующим образом.

1. Алиса генерирует другое простое число 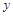, вычисляет число 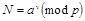и посылает его Бобу. (То есть она передает Бобу изоморфную трудную задачу).

2. Боб может попросить Алису:

а) открыть 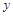, то есть дать решение изоморфной трудной задачи;

б) открыть 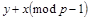, то есть логарифм произведения MN.

3. Алиса выполняет просьбу Боба, и шаги протокола повторяются при другом значении N.

Протоколы доказательства с нулевым знанием могут строиться также на основе использования свойств изоморфизма графов [11] и других трудных задач. В [11] рассмотрены также и слабости этих протоколов.

Итак, в криптографии известна и решена задача доказательства существования некоторой информации без раскрытия сведений о ней. К сожалению, идея доказательства с нулевым знанием не может быть непосредственно применена для построения системы ЦВЗ, из-за специфики последней. Далее рассмотрена эта специфика и возможные модификации протокола доказательства с нулевым знанием для применения в ЦВЗ [14].

В рассмотренном выше протоколе Алиса имеет возможность публиковать открытое число M и различные значения N, а также 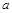 и . В случае же системы ЦВЗ вся эта информация должна встраиваться в изображение. Если ее сделать доступной для Боба, тот может просто удалить ее из изображения, так как это не приведет к существенному ухудшению его качества. Возможным выходом являлось бы использование надсознательного канала, то есть ЦВЗ в виде хэш-функции от наиболее значимых признаков изображения. В этом случае удаление ЦВЗ приведет к значительной деградации изображения. Однако, таким образом невозможно встраивать новую информацию, например, вычисленное значение M. По существу, надсознательный канал доступен для Алисы в режиме «только для чтения».

Вначале рассмотрим возможную реализацию протокола с нулевым знанием в известной схеме построения системы ЦВЗ, носящей имя Питаса [15]. В основе схемы Питаса лежит разделение всего множества пикселов на два подмножества, увеличение значений на некоторое число k в одном подмножестве и уменьшение на то же число k - в другом. Таким образом, средние значения двух подмножеств будут отличаться на 2k.

Версия схемы Питаса для протокола с нулевым знанием строится следующим образом. После внесения ЦВЗ в контейнер Алиса выполняет перестановку 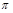. Затем она доказывает наличие перестановки ЦВЗ 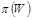в перестановке контейнера 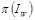без раскрытия значения ЦВЗ W. Для исключения обмана с ее стороны Алиса должна опубликовать множество сигналов 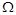таких, что их скремблированные значения дают множество всех возможных ЦВЗ.

Итак, в соответствии с [14]:

1. Алиса генерирует перестановку, вычисляет последовательность 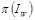и посылает ее Бобу.

2. Боб теперь знает, как исходный контейнер, так и его перестановку и случайным образом просит Алису:

а) открыть перестановку, чтобы убедиться что нет обмана;

б) показать наличие 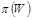в .

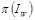3. Алиса выполняет просьбу Боба.

4. Алиса показывает, что она не смошенничала и 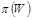действительно является перестановкой ЦВЗ. Для этого она предъявляет допустимую процедуру скремблирования 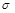, такую что .

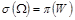5. Использованная перестановка больше в протоколе не применяется.

Данный протокол порождает ряд проблем. Во-первых, даже небольшой сдвиг контейнера приведет к рассогласованию значени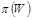й и 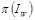. В принципе, эта проблема не самого протокола. Она вызвана чувствительностью схемы Питаса к пространственным сдвигам. Другая проблема состоит в некоторой «утечке» информации о выполненной Алисой перестановке. Дело в том, что значения интенсивностей пикселов при перестановке не изменяются, и атакующий будет использовать эту информацию для сужения круга возможных перестановок. Еще одна слабость протокола заключается в том, что Алиса может найти и использовать такие перестановки, что 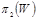будет отыскиваться в 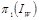, и Боб не сможет обнаружить мошенничество.

Поэтому, в [14] был предложен ряд усовершенствований вышеприведенного стеганографического протокола с нулевым знанием, с использованием криптографически сильных перестановок, основанных на сложных проблемах, например, поиска путей на графах.

Данный текст является ознакомительным фрагментом.