Нечеткая логика

Нечеткая логика

Первые работы по нечеткой логике были опубликованы в 1965 году профессором Калифорнийского университета в Беркли Лотфи Заде. С самого начала принципы нечеткой логики как усиленно рекламировались, так и подвергались критике.

В сущности нечеткая логика пытается имитировать подход человека к определению групп и классов явлений. Определение «нечеткости» можно пояснить некоторыми примерами. Например, на основе какого критерия теплый солнечный день может быть определен, не как «теплый», но как жаркий и кем? Основанием, на котором кто-то определяет теплый день как жаркий, может служить персональное ощущение тепла, которое в свою очередь зависит от его или ее окружения (см. рис. 6.27).

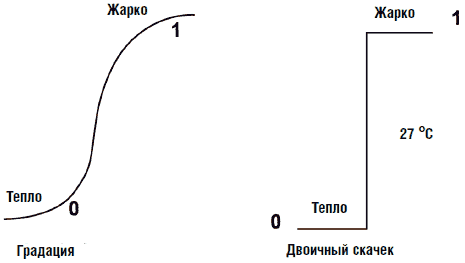
Рис. 6.27. Изменение температуры от теплой до жаркой: плавно или скачком

Не существует универсального термометра, который «утверждает», что 26,9 С° это тепло, а 27 С° уже жарко. Если рассмотреть этот пример шире, то люди, населяющие Аляску, будут иметь иной интервал температур для «теплых дней» в сравнении с жителями Нью-Йорка, и оба эти значения будут отличаться от соответствующих значений для жителей Флориды. При этом еще не нужно забывать о временах года. Теплый зимний день отличается по температуре от летнего. Все сводится к тому, что основой классификации (например, понятия «теплый день») может служить интервал температур, определенных мнением группы людей. Дальнейшая классификация может быть проведена сравнением мнений различных групп людей.

Для любой температуры мы можем найти группу, в температурный интервал которой она попадает. В некоторых случаях температура может попасть в две пересекающиеся группы. Четкая принадлежность к группе может быть определена по отклонению значения от среднего по группе.

Идея групповой или интервальной классификации может быть расширена на многие другие вещи, такие как ориентирование, скорость или рост. Давайте используем понятие роста для еще одного примера. Если мы построим график роста 1000 людей, его форма будет напоминать первую кривую на рис. 6.28. Мы можем использовать этот график для формирования групп людей маленького, среднего и высокого роста. Если мы применим жесткое решающее правило считать всех ниже 170 см людьми низкого роста и всех выше 180 людьми высокого роста, то график примет форму 2 на рис. 6.28. Такое правило считает рост 178 см «средним», хотя в действительности человек такого роста находится ближе к группе «высоких» (от 180 см и выше).

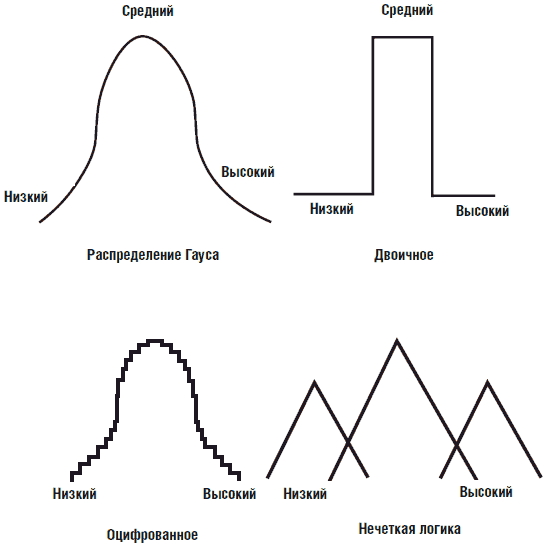
Рис. 6.28. Группировка людей по росту на основании различных правил

Вместо правил жесткой «быстрой» логики, обычно используемой в компьютерах, человек, как правило, использует более «мягкую», неточную логику или нечеткую логику. Для введения нечеткой логики в компьютер мы определим сами группы и степень принадлежности к группе. Таким образом, человек ростом 178 см почти не будет принадлежать группе людей среднего роста (слабое присутствие) и уверенно принадлежать группе высокого роста (сильное присутствие).

Нечеткая логика представляет собой альтернативу оцифрованному графику, представленному под номером 3 на рис. 6.28. График, оцифрованный с высоким разрешением, позволяет измерять рост с такой же точностью. Какова причина применения нечеткой логики вместо использования оцифрованной модели? Дело в том, что методы нечеткой логики требуют более простых форм математического обеспечения и функций научения.

Для моделирования нечеткой логики в PIC микроконтроллере для групп необходимо создать численные интервалы значений. Этим мы займемся в следующем проекте.

Данный текст является ознакомительным фрагментом.