2. Свет и телевидение

2. Свет и телевидение

Да будет свет.

Немного истории

Свет — это одно из основных и величайших явлений природы, свет является не только необходимым условием жизни на планете, но и играет важную роль в техническом прогрессе и изобретениях в сфере визуальной коммуникации: фотографии, кинематографии, телевидении и недавно появившихся мультимедийных средствах.

Хотя явление это «базовое», и мы видим его все время и всюду, но в науке — это самый большой камень преткновения. Физика, которая в конце XIX века представляла собой довольно простую, непосредственную науку, стала сложной и мистической. Ученым в начале XX века пришлось ввести постулаты квантовой физики — «принципы неопределенности» и многое другое. И все это для того, чтобы получить теоретический аппарат, который объяснил бы множество экспериментов и, в то же время, имел бы разумный смысл.

В этой книге мы не намерены углубляться во все эти теории: мы обсудим только те вопросы, которые связаны с телевидением и передачей видеосигналов.

Основная «проблема», с которой сталкиваются ученые, изучающие свет, заключается в том, что свет имеет двойственную природу: он ведет себя как волна (нематериальная природа) — это явления рефракции и отражения — и обладает также свойствами материальной природы — широко известный фотоэффект, открытый Генрихом Герцем в XIX веке и объясненный Албертом Эйнштейном в 1905 г. Поэтому в последнее время в физике принято полагать, что свет имеет «двойственную» природу.

На этом этапе следует отдать должное, по крайней мере, нескольким самым крупным ученым-физикам, и, в частности, специалистам по теории видимого излучения, без работ которых современный уровень технологий был бы невозможен.

Одним из первых физиков, объяснивших многие природные явления, включая и свет, был Исаак Ньютон. В XVII веке он доказал, что свет имеет корпускулярную природу. И так считалось до Христиана Гюйгенса, который позже, но тоже в XVII веке, выдвинул волновую теорию света. Многие ученые глубоко уважали Ньютона и не изменили своих взглядов до самого начала XIX века, когда Томас Юнг продемонстрировал интерференцию света. Август Френель тоже проделал ряд убедительных экспериментов, четко демонстрирующих волновую природу света.

Важной вехой стало появление на научной сцене Джеймса Кларка Максвелла: в 1873 г. он доказал, что свет представляет собой высокочастотную электромагнитную волну.

С помощью его теории удалось оценить величину скорости света, как она известна нам сегодня: 300 000 км/сек. Эксперименты Генриха Герца подтвердили теорию Максвелла. Герц открыл явление, которое известно как фотоэффект: свет может выбивать электроны с освещаемой металлической поверхности. Однако ему не удавалось объяснить тот факт, что энергия испускания электронов не зависит от интенсивности света, что в свою очередь противоречило волновой теории. С точки зрения волновой теории, большая интенсивность света должна увеличивать энергию испускаемых электронов.

Этот камень преткновения удалось обойти Эйнштейну: он использовал разработанную Максом Планком теорию квантования энергии фотонов, представляющих минимальную порцию переносимой светом энергии. В рамках этой теории свет обрел свою двойственную природу, т. е. сочетание волновых и корпускулярных свойств.

Таким образом, эта теория наилучшим образом объясняет большинство световых явлений, и поэтому в CCTV (замкнутое, кабельное охранное телевидение или видеонаблюдение) мы будем использовать теорию «двойственного подхода».

При анализе линз, используемых в системах видеонаблюдения, мы будем в большинстве случаев опираться на волновую теорию света, но при этом не следует забывать и о том, что есть такие понятия, как функционирование ПЗС-матриц, например, отражающее корпускулярную природу света, т. е. его материальную природу. Поэтому в этих случаях мы будем использовать корпускулярный подход.

Естественно, что в реальности свет требует применения обоих подходов, и мы всегда должны помнить о том, что они не являются взаимоисключающими.

Основы теории света и глаз человека

Свет — это электромагнитное излучение. Человеческий глаз может реагировать на это излучение и различать частоты, которые воспринимаются глазом как цвет. Посмотрите на рис. 2.1 электромагнитное излучение включает все частоты, или длины волн. Видимый свет занимает лишь небольшое «окно» этого диапазона. Это окно лежит в диапазоне от 380 нм до 780 нм. Чтобы легче было запомнить, мы приближенно примем границы диапазона равными 400 нм и 700 нм. 400 нм соответствует фиолетовому цвету, а 700 нм — красному. По мере увеличения длины волны цвет непрерывно переходит от фиолетового к голубому, зеленому, желтому, оранжевому и красному. Для определения средней чувствительности человеческого глаза было проделано множество экспериментов и тестов, и, как видно из рисунка, не все цвета оказывают одинаковое воздействие на сетчатку глаза.

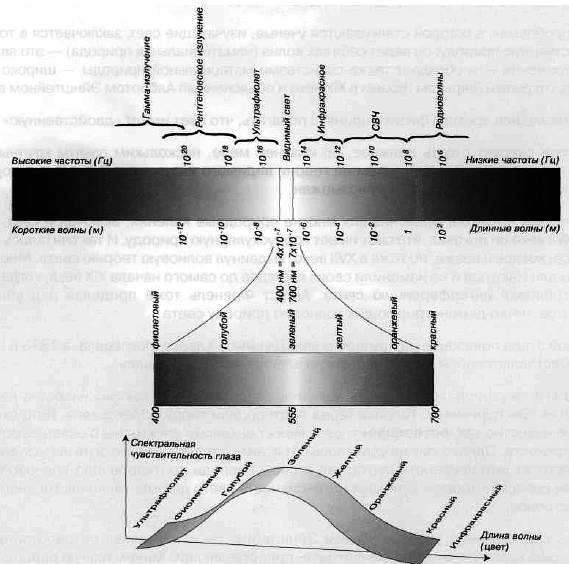
Рис. 2.1. Электромагнитный спектр и чувствительность человеческого глаза

Глаз наиболее чувствителен к зеленому цвету. Другими словами, если собрать все длины волн с равной энергией, то зеленый будет иметь наибольший «выход» на сетчатке. Частоты выше фиолетового (длины волн короче 400 нм) и ниже красного (длины более 700 нм) не воспринимаются «средним» человеческим глазом. Я подчеркиваю здесь «средним», потому что чувствительность человеческого глаза — это статистическая величина. Есть люди с «цветовой слепотой», чья спектральная чувствительность отличается (обычно уже) от показанной на рисунке. Некоторые люди с «цветовой слепотой» не видят красный цвет, другие не различают голубой. Натренированный профессиональный глаз художника или фотографа может развить очень высокую чувствительность, различая такие частоты (цвета), которые другим могут казаться одинаковыми. Некоторые могут даже выйти за минимальный и максимальный предел воспринимаемых частот, то есть различать темно-фиолетовый или красный цвет, невидимый для других индивидов.

Есть один интересный вопрос, который мы можем задать сами себе: почему максимум спектральной чувствительности лежит в зеленом цветовом диапазоне (около 555 нм)? Возможно, это связано с тем фактом, что большая часть солнечной энергии, проникающей в атмосферу Земли, сконцентрирована на длинах волн порядка 555 нм.

В течение миллионов лет, когда проходила эволюция жизни на планете, у нас (и почти у всех животных) развивалось зрение, способное воспринимать те длины волн, которые были наиболее доступны (по крайней мере, в дневное время). Альтернативой является ночное зрение животных, которые охотятся на теплокровных млекопитающих. Тепло, излучаемое телом, — это и есть инфракрасная радиация. Вот типичные представители: змеи, кошки и совы. Некоторые змеи, к примеру, кроме глаз для общего зрения, обладают инфракрасно-чувствительными органами, при помощи которых змея может определить температурные изменения менее 0.5 °C (1° F). Кошки, в том числе и дикие — леопард, пума и другие члены семейства кошачьих, известны своим прекрасным ночным зрением, а это означает, что их реакция в ближнем инфракрасном диапазоне намного лучше, чем реакция человеческого глаза.

Мы остановимся на глазе человека, а для этого важно понимать его «конструкцию».

Эти вопросы и сами по себе интересны, но, кроме этого, мы найдем еще и массу концептуальных аналогий между устройством глаза и ТВ-камеры.

На рис. 2.2 мы видим глазную линзу (хрусталик), которая и фокусирует изображение на сетчатке.

Сетчатка — это на самом деле «фоточувствительная область», состоящая из миллионов клеток — колбочек и палочек. Эти клетки можно рассматривать как часть нашей нервной системы. Колбочки чувствительны к средней и яркой интенсивности света и воспринимают цвета. Палочки чувствительны к низким уровням света и не способны различать цвета. Ночью мы видим благодаря палочкам, поэтому в темноте мы не можем различать цвета.

Число колбочек в каждом глазе приблизительно составляет 10 млн., а палочек — около 100 млн. Колбочки сконцентрированы вокруг области прохождения оптической оси. Эта область окрашена желтым пигментом и называется желтым пятном. Желтое пятно является основной областью, которую обрабатывает наш мозг, и, хотя она очень мала, концентрация колбочек в ней составляет около 50 000. Среднее фокусное расстояние глаза (то есть расстояние между хрусталиком и сетчаткой при разглядывании бесконечно удаленного объекта) составляет около 17 мм. Такое фокусное расстояние дает резкое изображение в пространственном угле, равном примерно 30°. Это также и размер области, где больше всего колбочек. Именно поэтому угол в 30° считается стандартным углом зрения.

Концентрация колбочек возрастает по направлению к центру оптической оси, достигая максимума лишь на 10°. Каждая из клеток-кол бочек соединяется с мозгом отдельным зрительным нервом, по которому электрические импульсы посылаются в мозг. Конечно, глаз видит и под гораздо большим углом, так как сетчатка охватывает пространственный угол почти в 90°, и колбочки есть и вне желтого пятна, но к одному нерву в этом случае подсоединена группа колбочек. В этой области мы видим не так четко, как в области, где к каждой колбочке подсоединен отдельный нерв, поэтому эта часть сетчатки называется областью периферического зрения.

Рис. 2.2. Схема устройства глаза

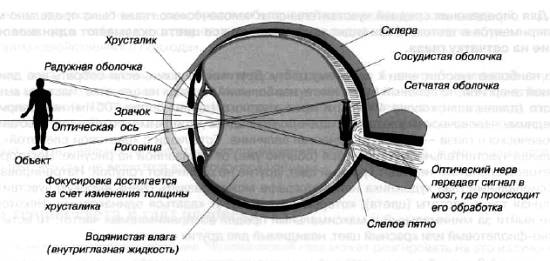
Рис. 2.3. Аналогии между устройством глаза и камерой

«Секция обработки изображения» в головном мозге сконцентрирована на 30°, хотя видим мы лучше примерно на 10°. Обработка поддерживается постоянными движениями глаза во всех направлениях, что аналогично панорамной головке в видеонаблюдении.

В SLR-камерах (однообъективных зеркальных фотоаппаратах) стандартный угол зрения в 30° достигается при помощи 50-мм объектива, для 2/3" камеры — это 16-мм объектив, для 1/2" камеры — 12-мм и для 1/3" камеры — 8-мм объектив. Другими словами, изображения, полученные при помощи любого типа камер с соответствующими стандартными объективами, будут иметь довольно близкие размеры и перспективу, похожую на то, что мы видим своими глазами.

Объективы с меньшим фокусным расстоянием дают более широкий угол зрения и называются широкоугольными объективами. Объектив с большим фокусным расстоянием сужает угол зрения, и поэтому кажется, что он приближает удаленные объекты, отсюда и название: телеобъектив («теле» означает далекий). Еще один интересный вопрос, касающийся видеонаблюдения, связан с тем, что, зная фокусное расстояние глаза и максимальный диаметр раскрытия радужной оболочки, равный примерно 6 мм, мы можем найти эквивалентное F — число глаза (которое мы обсудим позже в этой книге):

F_глаза= 17/6 = 2.8

С полностью раскрытой радужной оболочкой мы можем довольно хорошо видеть в полнолуние (освещенность объектов равна примерно 0.1 люкса). Помните это число, когда будете сравнивать минимальные характеристики освещенности для разных камер.

Фокусировка, которую выполняет глаз, чтобы человек мог видеть объекты на различных расстояниях, достигается за счет изменения толщины хрусталика (линзы). Толщина хрусталика меняется цилиарными мышцами. Если глаз в порядке, он может фокусироваться от бесконечности до минимального расстояния, равного примерно 20 см в раннем детстве, 25 см — в возрасте 20 лет, 50 см — в 40 лет и 5 м — в 60 лет. Если мы смотрим на очень удаленный объект, то есть глаз фокусируется на бесконечность, цилиарные мышцы расслабляются, и линза становится тонкой.

Если же глаз не может фокусироваться на бесконечности, то такой дефект зрения называется близорукостью или миопией. В этом случае нужны очки, которые помогут «дефективной» глазной линзе сфокусировать изображение на сетчатке. Такие очки иногда называют уменьшающими очками, потому что они имеют отрицательный фокус (или диоптрии).

Диоптрия — это величина, обратная фокусному расстоянию линзы, где фокус выражен в метрах.

Уменьшающие очки имеют отрицательные диоптрии. Итак, «уменьшающие» очки в -0.5 диоптрий, например, имеют отрицательный фокус, равный 1/(-0.5) = -2 м.

Другой дефект глаза заключается в том, что глаз не может сфокусироваться на очень близком изображении, то есть глазная линза по тем или иным причинам не может стать достаточно толстой. Этот дефект называется дальнозоркостью или гиперметропией.

Людям с гиперметропией, чтобы разглядеть близкие предметы, требуются очки. Такие очки должны иметь характеристики, противоположные рассмотренным выше, то есть они должны увеличивать изображение и иметь положительный фокус (или диоптрии).

Когда мы смотрим на объект двумя глазами, то в мозг проецируется зрительный образ, создающий стереоскопический эффект, и мы воспринимаем объемность пространства. Если прикрыть один глаз, то будет очень трудно воспринимать «трехмерность» окружающего нас пространства.

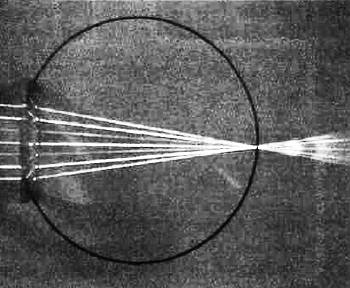
Рис. 2.4. Как работает глаз

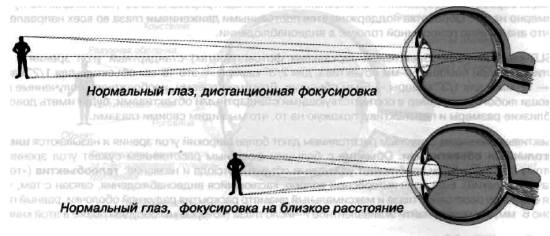
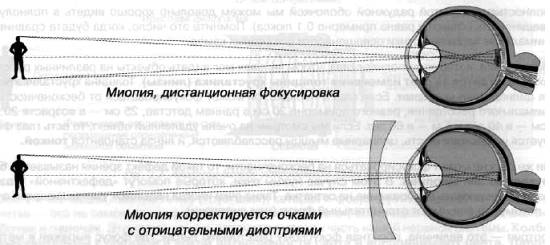
Рис. 2.5. Корректирование дефектов зрения при помощи очков

Расстояние между глазами (60–70 мм) обеспечивает наше восприятие трехмерного пространства вплоть до 10–15 метров. На более далеком расстоянии очень трудно судить, какой из двух предметов ближе. Вы можете провести такой эксперимент: посмотрите на два достаточно удаленных от вас, но удаленных на разные расстояния, находящиеся в воздухе объекта. Если мы смотрим, скажем, на два дерева, мозг делает заключение о расстоянии на основе земли и перспективы того, что находится перед нами, но перспективное «решение» в этом случае будет сделано не на основе «стереоскопического механизма» глаза.

Когда задумываешься о сложности строения глаза и мощности мозга при «обработке изображений», не перестаешь удивляться. Мы проделываем эти операции сотни раз на дню и даже не думаем об этом.

Не говоря уже о том, что изображение на сетчатке перевернуто, ведь такова природа оптической рефракции, и мы совершенно не замечаем мелких движений глаза, которые происходят во всех направлениях, когда мы смотрим на что-то. Все это расшифровывается и контролируется мозгом.

Конфигурация «глаз/мозг» намного совершеннее любой камеры, которую человек изобрел или изобретет в будущем. Но как люди техники, мы можем сказать, что понимание «работы» глаза и использование непрерывно усовершенствующихся визуальных технологий как на уровне технического, так и на уровне программного обеспечения, позволяет нам получать более совершенные изображения и более полную информацию об окружающем мире. Мы можем видеть вещи, недоступные человеческому глазу, и отслеживать объекты в таких местах, где человек не может находиться.

Рис. 2.6. Разрешающая способность человеческого глаза

Многочисленные эксперименты и тесты показали, что человеческий глаз может различить самое большее 5–6 пар линий на миллиметр. Этот показатель подразумевает оптимальное расстояние между глазом и объектом 30 см, то есть, когда мы, например, читаем достаточно мелкий текст. Это дает минимальный угол примерно в 1/60 градуса. Таким образом, это значение 1/60 градуса считается пределом угловой разрешающей способности для нормального зрения. Мы можем использовать угловую разрешающую способность глаза для лучшего понимания того, как человек воспринимает мелкие детали, что затем позволит нам применить наши теоретические познания на практике.

При расчете оптимальной дистанции между наблюдателем и монитором существует простая рекомендация, которая предписывает умножать высоту экрана монитора на семь. Подробнее о мониторах читайте в соответствующей главе этой книги. Вообще, необходимо понимать, что расстояние до монитора — это крайне важный аспект психофизиологического восприятия деталей в изображении. Человеку, который смотрит в монитор, совершенно не нужно находиться слишком близко к экрану, но и очень далеко от экрана располагаться зрителю тоже не стоит.

Световые единицы

Свет — это физическое явление, интерпретируемое психологическими процессами в нашем мозге. И поэтому его сложнее оценивать или измерять, чем любой другой физический процесс. Чтобы проделать объективные измерения, необходимы некоторые предварительно заданные условия.

Одно из них — это полоса рассматриваемых частот излучения, обычно лежащая в пределах от 400 нм до 700 нм. Все частоты вносят свой вклад в световую энергию, излучаемую источником.

Для начала давайте рассмотрим различные типы источников света.

Обычно их делят на две основные группы:

— первичные источники (солнце, уличное освещение, лампы накаливания, ЭЛТ-мониторы);

— вторичные источники (все объекты, которые не генерируют свет, а только отражают).

Для измерения количества света, излученного, например, лампой накаливания, и света, отраженного от объекта, мы применяем различные способы. И если мы анализируем свет, испускаемый источником во всех направлениях и в узком телесном угле, — то это совсем не одно и то же. Есть несколько причин того, почему мы используем различные единицы измерения света.

Наука, изучающая все эти аспекты, называется фотометрией, а соответствующие единицы измерения — фотометрическими единицами.

Различные ученые, в зависимости от своих взглядов, вводили различные единицы света. Поэтому возникают определенные трудности при попытке понять или описать характеристики телекамер. Но давайте все-таки попробуем пролить свет на эти вопросы и объяснить, что есть что. Начнем в логическом порядке, то есть вначале рассмотрим источники света, затем распространение света в пространстве, падение на объект и, наконец, отражение.

Сила света (/) характеризует световую энергию первичного источника, излучающего во всех направлениях. Единица измерения силы света — кандела (кд). Одна кандела примерно равна количеству световой энергии, испускаемой обычной свечой. В 1948 г. появилось более точное определение канделы: кандела — это сила света, излучаемая черным телом, нагретым до температуры перехода платины из жидкого в твердое состояние.

Световой поток (F) — это сила света в некотором телесном угле. И, следовательно, единица светового потока получается делением силы света на 4? радиан (в сфере 4? = 12.56 стерадиан) и измеряется в люменах (лм). Один люмен — это световой поток, испускаемый источником с силой света в 1 кд внутри единичного телесного угла (угла в 1 стерадиан).

Поскольку ощущение яркости зависит от чувствительности человеческого глаза, то световой поток зависит также и от длины волны. Например, свет мощностью в 1 ватт на 555 нм (зеленый цвет) дает световой поток приблизительно равный 680 лм, а все другие длины волн с такой же силой света дают меньший световой поток (см. кривую спектральной чувствительности глаза). Поэтому бессмысленно выражать энергию света в ваттах, несмотря на то, что теоретически световая энергия, как и любой другой вид энергии, может быть выражена в ваттах.

Освещенность (Е) — это наиболее часто используемый в видеонаблюдении термин, особенно при описании характеристик минимальной освещенности камер. Освещенность очень похожа на яркость, за исключением того, что в этом случае имеются в виду объекты, являющиеся вторичными источниками света.

Итак, освещенность поверхности — это величина светового потока, приходящегося на единицу площади.

Если световой поток в 1 люмен падает на поверхность площадью в 1 м² (квадратный метр), он измеряется в люменах на квадратный метр или метр-свечах, более известных под названием люкс (лк). Это означает, что если у нас есть сфера радиусом 1 метр и источник света с силой света в 1 канделу, расположенный внутри сферы, то освещенность на внутренней поверхности сферы будет равна 1лк. Математически это соотношение может быть записано следующим образом:

E = Flux/Area = F/A [лк] (1)

Поток F_по определению равен силе света, умноженной на телесный угол, то есть:

F = I?? [лм] (2)

Предполагая, что источник света является точечным, и, опираясь на формулы сферической тригонометрии, мы можем выразить ? через освещаемую площадь А и расстояние до источника d:

? = A/d²[рад] (3)

Подставив (2) и (3) в (1), получаем:

E = I/d² [лк] (4)

Это означает, что освещенность перпендикулярной площадки обратно пропорциональна квадрату расстояния до источника. Если же площадка расположена под некоторым углом к падающему свету, то мы можем оценить действительную поверхность, сделав проекцию на угол ? как на схеме на рис. 2.7. В этом случае формула (4) принимает вид:

E = I?cos ?/d² [лк] (5)

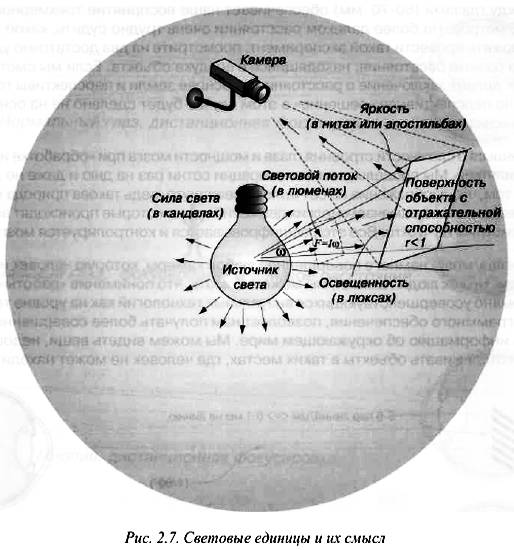
Типичные уровни освещенности приведены на рисунке 2.8.

Рис. 2.8. Некоторые типичные уровни освещенности

Очень редко, в малых областях пространства и при очень сильных источниках света могут обеспечиваться уровни освещенности выше 100 000 лк (например, вблизи сильной импульсной лампы).

Для описания таких освещенностей иногда используются другие, более крупные единицы — фоты.

Один фот равен 10 000 лк.

В американской терминологии, где все еще широко используется квадратный фут вместо единиц СИ, освещенность выражается в канделах на квадратный фут, или фут-свечах. Поскольку соотношение между квадратным метром и квадратным футом равно примерно 10 (или точнее 9.29), то довольно просто перевести люксы в фут-свечи и наоборот. Если освещенность задана в фут-свечах, достаточно разделить эту величину на 10, и вы получите приблизительное значение в люксах, а если значение задано в люксах, то, чтобы перевести его в фут-свечи, умножьте его на 10.

Термин Яркость (L) характеризует свечение поверхности первичного или вторичного источника света. Поскольку свечение имеет субъективный подтекст, то в качестве объективного, научного термина используется понятие «яркость». Яркость зависит от силы света самой поверхности и от угла наблюдения, поэтому рассчитывается на единицу перпендикулярной направлению взгляда площадки. Существует всего несколько единиц яркости. Предпочитаемся в мире метрическая единица яркости — это нит. Один нит равен одной канделе на квадратный метр спроектированной площадки (I/A). Если для измерения светового потока источника вместо кандел использовать люмены, то яркость будет выражена в апостильбах (асб). Все становится несколько более сложным, если мы имеем дело с поверхностью, на которую световой поток падает под углом ? к нормали (или отражается); в этом случае световой поток прямо пропорционален cos?. Тогда со всех направлений будет казаться, что поверхность имеет одинаковую яркость, потому что и отраженный свет, и спроектированная поверхность подчиняются одним и тем же тригонометрическим законам. Такой тип поверхности называется ламбертовским радиатором или рефлектором (в зависимости от того, является ли поверхность первичным или вторичным источником света) и обычно описывается как равномерно рассеивающая поверхность. Для измерения яркости в этом случае в метрическую систему была введена еще одна единица — ламберт. Эквивалентная американская единица — фут-ламберт.

То, какова будет освещенность, воспринимаемая камерой, на самом деле зависит от силы света самого источника и от отражательной способности освещаемого объекта. Объект может быть черным или белым и, понятно, что это не одно и то же. Если объекты белые, то, естественно, при одном и том же количестве света мы сможем видеть больше. Поэтому, говоря об освещенности, необходимо ввести еще один фактор: коэффициент отражения, выраженный в процентах. Определение коэффициента отражения можно задать следующим простым соотношением:

р = отраженный от поверхности свет/падающий на поверхность свет = E/L [%] (6)

На практике эта величина меняется от очень низкого значения в 1 % для черного бархата, 32 % для обычной поверхности почвы до 93 % для чистого белого снега. Кожа человека европеоидной расы имеет коэффициент отражения от 19 до 35 %. Испытательная таблица CCTV Labs, которая напечатана на обложке этой книги, имеет коэффициент отражения около 60–70 %.

Этот фактор очень важен при определении минимальной освещенности камеры, так как при одинаковом уровне освещенности, но различных коэффициентах отражения, объекты будут иметь различную яркость, косвенно влияя на производительность камеры.

Измерение освещенности с помощью экспонометра

Очень часто нам необходимо измерить освещенность того или иного объекта. Для этого мы можем воспользоваться люксметром, который предназначен именно для таких измерений. Когда вы пользуетесь люксметром, то первое, на что следует обратить внимание, это его диапазон измерений. С помощью типичного люксметра вы можете проводить измерения освещенности не более 1 люкса (для большинства случаев этого вполне достаточно).

При низком уровне освещенности менее 1 люкса (в условиях ночной видимости) мы уже не сможем пользоваться таким люксметром, но вместо него можно взять более качественный и дорогой фотоэкспонометр. В продаже имеется несколько известных марок, таких, как Sekonic, Minolta и Gossen, и некоторые из них выдают результаты измерения сразу в люксах.

Впрочем, если у вас не оказалось под рукой люксметра, то можно обойтись и обычным зеркальным фотоаппаратом, а точнее — его встроенным экспонометром, хотя результаты измерений и не будут выражаться в люксах.

Это может оказаться очень удобным инструментом, поэтому далее я объясню принципы и формулы, по которым вы сможете перевести полученные результаты в люксы.

Стоит заметить, что большинство зеркальных фотоаппаратов имеют встроенный люксметр, тогда как в других типах фотоаппаратов его может и не оказаться. Поэтому если на вашем фотоаппарате нет никаких индикаторов для exposure and aperture, то для измерения освещенности он непригоден. Также следует напомнить, что для более аккуратных измерений логично использовать фотокамеру с таким же полем зрения, как и у предполагаемой телекамеры, для которой мы проводим измерения.

По этой причине лучше иметь трансфокатор, что позволит нам подобрать поле зрения примерно такое же, как и у предполагаемой телекамеры.

Для начала давайте немного освежим нашу память и вспомним некоторые общие принципы экспозиции фотографической пленки.

На всех фотоаппаратах индикаторы выдержки указывают время в секундах, а точнее сказать — в долях секунды. Таким образом, когда мы видим, что индикатор выдержки показывает число 125, это на самом деле означает, что установлена выдержка длительностью 1/125 секунды. Чтобы избежать путаницы при длительной выдержке, когда время указывается в секундах, после числа ставится буква «s», то есть «2 s» обозначает выдержку длительностью 2 секунды. Стандартным временем выдержки считаются следующие значения: 1; 2; 4; 8; 15; 30; 60; 125; 250. Все это, разумеется, доли секунды. Впрочем, существуют и модели фотоаппаратов, которые позволяют выставить выдержку более 1 секунды и менее 1/1000 секунды. Как вы уже, вероятно, заметили, значения выдержки выбраны таким образом, что каждое следующее значение примерно в два раза короче предыдущего.

Индикатор диафрагмы показывает значения в F-числах. Так число «5.6» обозначает F-5.6. Чем больше это число, тем меньше раскрыта диафрагма. Стандартными значениями здесь будут 1.0; 1.4; 2; 2.8; 4; 5.6; 8; 11; 16; 22; 32 и 44. Для каждого последующего F-числа раскрытие диафрагмы будет в два раза меньше, чем у предыдущего, то есть каждое последующее F-число будет пропускать в два раза меньше света, чем предыдущее в приведенной последовательности.

Для выбора правильной экспозиции в вашем фотоаппарате имеется экспонометр, который выставляет корректные значения выдержки и диафрагмы. В автоматическом режиме оба значения определяются автоматически. В режиме приоритета диафрагмы мы выбираем F-число, а электроника фотоаппарата рассчитывает и устанавливает длительность выдержки. И, наконец, в режиме приоритета выдержки все происходит наоборот. Здесь мы вручную выбираем длительность выдержки, а F-число устанавливается автоматически.

Имеются разные комбинации времени выдержки и F-числа, при которых, тем не менее, на пленку будет попадать равное количество света. Например, если на вашем фотоаппарате установлена комбинация 1/30 с и F-5.6, то на пленку попадет примерно такое же количество света, как и при комбинации 1/60 с и F-4. Конечно, в последнем случае у нас будет немного меньшая глубина резкости с меньшим F-числом, но в остальном пленка будет экспонирована корректно. Учитывая факт равенства количества света с разными комбинациями выдержки и F-числа, эксперты из области фотографии рекомендовали специальную таблицу экспозиционных чисел (EV, Exposure Value) для вычисления количества света, которое и измеряют экспонометры. Мы не будем вдаваться в подробности того, каким образом производятся измерения в фотоаппарате, так как это потребовало бы отдельной книги, но в общих чертах можно сказать, что существуют экспонометры интегральные, точечные, матричные и другие. В рамках данной книги нет смысла рассматривать их отличия, отметим лишь, что в большинстве фотоаппаратов используется как минимум интегральный экспонометр. Это вполне подходит для нашей сферы, так как в видеонаблюдении уровни освещенности могут быть определены только приблизительно.

Рис. 2.9. Индикация экспонометра в современном зеркальном фотоаппарате

Таблица 2.1. Перевод экспозиционного числа в люксы

В инструкции пользователя фотоаппарата обычно имеется таблица экспозиционных чисел, которая выглядит примерно так же, как и приведенная в нашей книге таблица.

В большинстве случаев таблица экспозиционных чисел относится к фотопленке (или к матрице, если у нас цифровой фотоаппарат) с чувствительностью 100 единиц ISO, а это достаточно стандартная фотопленка. По этой причине в наших дальнейших вычислениях мы будем считать, что в нашем фотоаппарате заряжена пленка именно с такой чувствительностью. Конечно, мы можем использовать пленку и с другой чувствительностью, но это потребует небольшой корректировки наших расчетов.

Таблицу экспозиционных чисел понять несложно.

Например, комбинация 1/30 с и F-5.6 дает экспозиционное число 10. То же самое число получится с комбинацией 1/60 с и F-4. Таблица экспозиционных чисел получается при суммировании порядковых номеров (Reference Numbers) для времени выдержки и F-чисел (RN_t + RN_f). Для удобства мы приводим и таблицу с порядковыми номерами выдержки и F-чисел. Например, в этой таблице длительности выдержки 1 секунда и диафрагме F-1.0 соответствует порядковый номер «О». Порядковый номер «1» соответствует длительности выдержки 1/2 секунды и диафрагме F-1.4, порядковый номер «2» — длительности выдержки 1/4 секунды и диафрагме F-2 и так далее по порядку.

Экспозиционные числа (EV) получаются сложением этих двух порядковых чисел. Например, экспозиционное число для комбинации выдержки 1/30 секунды и диафрагмы F-2.8 будет равно 8, так как порядковый номер для выдержки 1/30 секунды будет 5, а для диафрагмы F-2.8 это 3.

Приведу несколько простых формул (о них я уже писал в журнале «CCTV Фокус»), которые я вывел для приблизительного расчета порядковых номеров, если нет соответствующей таблицы под рукой:

RN_f = 6.7?lg(F — чиcло) (7)

F-число здесь соответствует тому, что нам выдает экспонометр фотоаппарата.

RN_t = -3.32?lg(t) (8)

t здесь соответствует реальной длительности выдержки, то есть если экспонометр нам показывает 125, то в формулу мы должны подставлять 1/125 секунды вместо t.

При желании можно подставлять и более привычное число 125 (назовем эту переменную «Т») вместо реальной длительности выдержки t, но тогда знак минуса перед логарифмом пропадает, и формула будет выглядеть так:

RN_T = 3.32?lg(T) (8a)

Не забудьте, что мы используем десятичные логарифмы.

Экспозиционное число (EV) вычисляется сложением двух полученных значений:

EV = RN_f + RN_t = 6.7?lg(F — число) — 3.32?lg(t) (9)

или, если мы используем ? вместо t:

EV = RN₁ + RN_T (9а)

Рассмотрим, как это делается, на практике.

Допустим, в мой фотоаппарат заряжена пленка с чувствительностью 100 единиц ISO, а встроенный экспонометр показывает значение выдержки 1/250 секунды и диафрагмы — F-8. В этом случае порядковые номера для выдержки и диафрагмы и экспозиционное число считаются следующим образом:

EV = RN1 + RNt = 6.7?lg(8) — 3.32?lg(1/250) = 6.7?0.9 + (-3.32)?(2.398) = 6 + 8 = 14

(результат мы округляем).

Зависимость между экспозиционным числом и освещенностью описывается следующим уравнением:

Iлк = 2.5 ? 2^{(RNf — RNt)} = 2.5?2^EV (10⁾

В правой части приведенного уравнения 2 возводится в степень экспозиционного числа (EV), полученное значение умножается на 2.5, и в результате мы получаем освещенность Ілк, выраженную в люксах. Например, если экспозиционное число фотокамеры будет 15, то соответствующая этому числу освещенность вычисляется как:

Iлк = 2.5?2¹⁵ = 81,192 лк

Конечно, в наших измерениях такая точность невозможна, так как мы не учитываем множество факторов, включая отражательную способность окружающих объектов, первичные источники света в поле зрения, которые сильно влияют на средний уровень освещенности, и т. д.

Поэтому полученный результат мы округляем до 82,000 лк.

Следует заметить, что «динамический диапазон» встроенных экспонометров может варьироваться в зависимости от модели фотоаппарата. Чем лучше фотоаппарат, тем шире диапазон его экспонометра. Также при применении наших инструкций по измерению чувствительности на практике не следует забывать о чувствительности фотопленки, которая должна быть 100 единиц ISO. Конечно, можно использовать фотопленку и с чувствительностью 200 единиц ISO, но при этом экспозиционное число будет сдвинуто на +1 значение, так как фотопленка 200 ISO в два раза чувствительнее фотопленки 100 ISO. Фотопленка 400 ISO в четыре раза чувствительнее фотопленки 100 ISO, и соответственно экспозиционное число будет сдвинуто на +2 значения. Например, если мы будем проводить наши измерения с фотопленкой 200 ISO и получим экспозиционное число 16, то это будет эквивалентно 15 с фотопленкой 100 ISO.

В заключение мы рассмотрим еще один практический пример.

Допустим, встроенный экспонометр моего фотоаппарата показывает выдержку 1/15 с и диафрагму F-2.8. В фотоаппарат заряжена фотопленка с чувствительностью 100 единиц ISO. В результате мы получаем экспозиционное число:

EV_(F-2.8+1/15) = 6.7?lg(2.8) — 3.32?lg(1/15) = 3 + 4 = 7

Что даст нам освещенность

Iлк = 2.5?2⁷ = 320 лк

Чтобы перевести это значение в фут-канделы, нужно разделить его на 10, что даст нам приблизительно 32 фут-канделы.

Большинство из нас, вероятно, знают, что в солнечный день уровень освещенности составляет примерно 100,000 лк, в обычном офисе — примерно от 100 до 1000 лк, а лунной ночью — около 0.1 лк и т. д.

В яркий солнечный день мы получим экспозиционное число порядка 15–16, тогда как для видеонаблюдения ночью при нормальном уличном освещении экспозиционное число будет 3, что при переводе даст нам 20 лк.

Не забывайте об ограниченном диапазоне измерений экспозиционного числа. У большинства фотоаппаратов диапазон измерений экспозиционного числа лежит в интервале от 1 до 20. Это означает, что самый низкий уровень освещенности, который вы сможете измерить таким фотоаппаратом, равен 5 лк. Этого будет вполне достаточно при проектировании большинства систем видеонаблюдения, но если вам необходимо измерить и более низкие уровни освещенности, то я рекомендую приобрести профессиональный люксметр или фотоэкспонометр.

Вычисление количества света, падающего на фотоприемник

Чтобы как следует себе представить «световой вопрос» с точки зрения камеры, нам нужно знать, какое количество света действительно падает на фотоприемник.

Величина освещенности на ПЗС-матрице (ИС на ПЗС) (или лицевой панели) Е_пзс в первую очередь зависит от яркости объекта L, а также от F-числа, т. е. собирающей способности линзы. Чем ниже F-число, тем больше света проходит через объектив (ниже мы еще рассмотрим этот вопрос). Эта величина также пропорциональна коэффициенту пропускания объектива т. А именно, в зависимости от качества стекла и производителя, а также от механики внутренних поверхностей, определенный процент света теряется в самом объективе.

Все вышеупомянутые факторы можно представить следующим соотношением:

Е_пзс = L????/4?F²) [лк] (11)

Ниже мы покажем, как выводится это соотношение, чтобы люди, используя эти формулы, могли четко понимать, что здесь предполагается, а что аппроксимируется (11). Но поскольку для этого требуются более сложные математические выкладки, то читатели, не испытывающие к этому интерес или не имеющие соответствующей базы, могут просто воспользоваться соотношением (11) как оно есть, помня при этом, что L — это средняя яркость объекта (в люксах), — это коэффициент пропускания объектива (в процентах), F— это F-число и равно 3.14.

Объект, находящийся в поле зрения камеры и освещенный источником света, испускает свет практически во всех направлениях, в зависимости от функции отражения. На практике объект с гладкими поверхностями в большинстве случаев может считаться ламбертовской равномерно рассеивающей поверхностью.

Тогда можно рассматривать поток, проходящий через полусферу радиуса r с центром ds. Пусть d? — это приращение угла ? к нормали, тогда поток в объеме, образованном вращением угла d? проходит через окружность на поверхности сферы, причем радиус окружности равен r d?, длина — 2??r²?sin??d?.

Рис. 2.10. Ламбертовская рассеивающая поверхность

Эта элементарная площадка на поверхности сферы задается следующим соотношением:

dA = 2??r²?sin??d? (12) и тогда телесный угол ?, стягиваемый конусом в центре сферы, задается соотношением:

? = dA/r² = 2??r²?sin??d?/r² = 2??sin??d? [стерадиан] (13)

поскольку сила света на ламбертовской поверхности (поток в стерадиане) в заданном направлении пропорциональна косинусу угла к нормали, а сила света полной поверхности в направлении нормали равна I, то под углом ? она будет равна I?cos?

Сила света dI элементарной площадки ds равна:

dI = I?cos??ds /s [люмен/стерадиан = кандел] (14)

поскольку I/s это действительная освещенность L в перпендикулярном направлении, то вышеприведенное соотношение принимает вид:

dI = L?cos??ds [кд] (15)

Элементарный поток dF равен элементарной силе света dI, помноженной на телесный угол:

dF = L?cos??ds?2??sin??d? [лм] (16)

Общий поток в конусе, образованном углом ? можно найти интегрированием от 0 до ?:

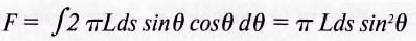
[лм] (17)

Если мы хотим найти полный световой поток, испускаемый во всех направлениях, то нужно положить угол ? равным 90°, тогда получим:

F_t = L???ds [лм] (18)

Теперь, если нам надо сосчитать поток в телесном угле, меньшем 90°, как это происходит в случае, когда камера направлена на объект, общий поток F_t задается формулой:

F₀ = ??L?ds₀?sin²?₀ [лм] (19)

Если коэффициент пропускания линзы равен ?, то поток, падающий на плоскость ПЗС (или лицевую панель), равен:

F_ПЗС = F₀?? = ????L?ds_0?sin²?₀

Освещенность ПЗС-матрицы (или лицевой панели) будет равна потоку, деленному на площадь, т. е.

E_ПЗС = ????L?ds₀?sin²?₀/ds_ПЗС [лк] (21)

Рис. 2.11. Вычисление светового излучения с помощью ламбертовской рассеивающей поверхности

Отношение (ds_ПЗС/ds₀₎, обратное которому использовалось в предыдущей формуле, известно как коэффициент увеличения объектива m. Коэффициент увеличения может быть также аппроксимирован как отношение между фокусным расстоянием линзы и расстоянием от линзы до объекта

m = (f/D)² = ds_ПЗС/ds₀ (22)

Когда мы произведем подстановку этих отношений в нашу основную формулу, то получим:

E_ПЗС = ????L?sin²?₀?(D/f)² [лк] (23)

Здесь потребуется ввести еще одно отношение, связанное с объективом (d/f), которое также известно как F-число объектива. Для объектов, которые расположены достаточно далеко от телекамеры (а это типично в большинстве случаев для систем видеонаблюдения) будет справедливо следующее:

tg?₀ = d/2D = sin?₀/cos?₀ = sin?₀ (24)

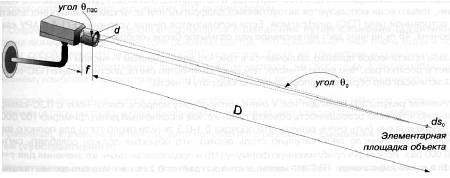
Рис. 2.12. Вычисление количества света, падающего на ПЗС-матрицу

Такое допущение имеет право на существование, потому что для очень больших расстояний до объекта угол ?₀ будет крайне мал, а значение косинуса этого угла будет стремиться к 1.

Таким образом, мы можем заменить sin²?₀ на (d/2D)², и наше уравнение примет следующий вид:

E_ПЗС = ????L?(d/2D)²?(D/f)² [лк] (25)

Это уравнение можно упростить:

E_ПЗС = ????L?(d²/4D²)?(D²/f²) = ????L?(d²/4f²) (26)

И, наконец, это уравнение преобразуется в упрощенную формулу для расчета количества света, попадающего в фотоприемник:

E_ПЗС = ????L?(4F²) [лк] (27)

Это очень удобная и полезная формула для приблизительного расчета освещенности фотоприемника, поскольку в ней используется только две переменные (яркость объекта и F-число объектива). Впрочем, не следует забывать: формула эта приблизительная, ее следует использовать только для грубых расчетов и только в тех случаях, когда выполняются условия, справедливые для вышеупомянутых допущений, то есть телекамера должна быть направлена на объект, рассеивающий свет примерно так же, как ламбертовская рассеивающая поверхность (в реальности так ведут себя большинство объектов, кроме зеркал и им подобных поверхностей), а сам объект должен быть расположен достаточно далеко (по сравнению с фокусным расстоянием) от телекамеры. Обычно коэффициент пропускания объектива меняется в пределах от 0.75 до 0.95.

Если производитель его не указывает, то для вычислений можно принимать значение 0.8.

Давайте рассмотрим пример. Пусть освещенность плоскости объекта составляет около 300 лк, как примерно в любом помещении офиса (пусть это будет E_object), яркость можно найти, используя коэффициент отражения окружающих объектов, т. е. L = E_object·р. Как уже упоминалось выше, различные объекты имеют различные коэффициенты отражения, но мы не далеко уйдем от реальности, если примем его равным 50 % для условий офиса. Если диафрагма объектива установлена на F/16, то освещенность ПЗС-плоскости будет составлять приблизительно Е_пзс = 0.8–3.14 — 300?0.5/(4 — 256) = 0.З блк. Это вместе с АРУ (AGC) камеры вполне реалистичная освещенность плоскости ПЗС-матрицы полного видеосигнала. Если же диафрагма объектива установлена на F/1.4, например, то освещенность ПЗС-плоскости будет равна примерно 48 лк (согласно соотношению (17)). Это значение гораздо выше необходимого для ПЗС-матрицы, и на практике она может дать узнаваемое изображение, только если используется автоустановка диафрагмы или если камера снабжена электронной встроенной (или ПЗС) диафрагмой. Если используется ручная установка F/1.4 и АРУ камеры отключена, 48 лк на чипе даст интенсивное или размытое белое изображение.

Базовое практическое правило заключается в том, что даже с низким F-числом объектив ослабляет свет в десятки раз. Чем выше F-число, тем ниже количество света, достигающего ПЗС-плоскости. Фактически оно обратно пропорционально квадрату F-числа.

Полученные результаты приводят нас к очень интересному вопросу, связанному с ПЗС-камерами (особенно ч/б): если освещенность объекта такая же, как в солнечный день (примерно 100 000 лк), то F-число должно быть очень велико. Это порядка 0.1–0.3 лк (или около того) для полного видеосигнала. Такое F-число действительно столь велико, что объектив должен ослаблять сигнал в 1 000 000 раз. Используя приближенную формулу (16) и предполагая такие же значения для ? = 0.8 и р = 0.5, а также имея в виду, что ПЗС-матрица камеры требует 0.2 лк на 1 Vpp сигнал, мы получим F-число, равное 886.

Это очень большое число для механических средств (листового затвора). Точность его движения ограничена, и, что еще более важно, при малых раскрытиях диафрагмы становится заметен нежелательный оптический эффект, называемый краевой рефракцией Френеля. На практике это означает, что очень высокие F-числа не могут быть достигнуты при использовании лишь механических методов. Поэтому используются специальные оптические фильтры нейтральной плотности (neutral density filter, ND), чтобы помочь затвору обеспечить высокие F-числа, требуемые для чувствительных ПЗС-матриц.

Для обеспечения полностью насыщенного сигнала в 1 Vpp на выходе камеры (с отключенной АРУ) в случае ч/б ПЗС-матриц Е_пзс должно быть около 0.1 лк. Некоторые производители приводят более низкие значения, ссылаясь обычно лишь на процент видеосигнала.

Цвет и телевидение

Цвет — очень важная и сложная проблема в видеонаблюдении. Хотя многие все еще предпочитают монохромные (ч/б) камеры, которые имеют более высокую чувствительность и реагируют на невидимый инфракрасный спектр, цветные камеры получают все более широкое распространение. За последние несколько лет, прошедшие со времени предыдущего издания книги, немало производителей стали предлагать так называемые камеры «день/ночь», которые автоматически переключаются в черно-белый режим, когда уровень освещенности падает ниже определенного значения.

Цвет дает ценную дополнительную информацию о наблюдаемых объектах. Но важнее то, что человеческий глаз фиксирует цветовую информацию быстрее, чем мелкие детали объекта. Впрочем, недостатком цветных телекамер были худшие (по сравнению с черно-белыми телекамерами) эксплуатационные показатели в условиях слабой освещенности. Это связано с использованием инфракрасного отсекающего фильтра на ПЗС-матрицах цветных телекамер, который ослабляет свет и убирает невидимое излучение инфракрасного диапазона. На этом мы остановимся более подробно в соответствующей главе, посвященной телекамерам, а сейчас отметим, что постоянное усовершенствование технологии ПЗС значительно улучшает работу цветной камеры при минимальном освещении. Если еще несколько лет назад мы имели показатель 10 лк @ F1.4, то сегодня могут «видеть» при 1 лк @ F1.4 на объекте и даже меньше.

Как уже говорилось, цвета, которые мы видим, соответствуют волнам света разной длины.

Например, видимый нами красный цвет — это излучение с соответствующими длинами волн, отраженное от красного объекта, на который падает белый свет. Черный поглощает волны почти любой длины, тогда как белый большинство из них отражает.

Наука цветов очень сложна, и становится еще сложнее, когда окружающие нас естественные цвета воспроизводятся при помощи покрытия ЭЛТ люминофором.