3.2.1. Формулировка задачи информационного скрытия при активном противодействии нарушителя

3.2.1. Формулировка задачи информационного скрытия при активном противодействии нарушителя

Используем традиционные для теоретического описания задач защиты информации обозначения. Рассмотрим обобщенную структурную схему стеганографической системы передачи скрываемых сообщений, представленную на рис. 3.1. Пусть источник контейнерных данных формирует случайную переменную 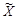, берущую значения в множестве 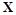в соответствии с общеизвестным распределением контейнера p( 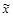), источник секретного ключа формирует стегоключ K, принадлежащий множеству 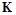, и источник скрываемых сообщений формирует сообщение М из множества сообщений М.

В задачах стеганографической защиты информации контейнер 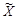есть блок данных или блок преобразованных данных (таких как коэффициенты дискретного косинусного преобразования или вейвлет — преобразования) изображений, видео, аудиосигналов, или некоторого другого множества контейнерных данных, в которые встраивается скрываемая информация. Алфавит 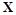может быть в зависимости от постановки задачи непрерывным (например, множеством неквантованных коэффициентов преобразования) или конечным дискретным (например, множеством квантованных коэффициентов преобразования).

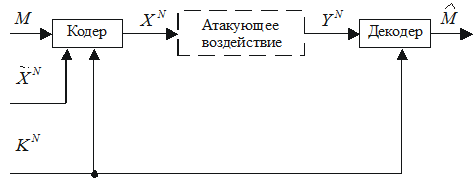
Рис. 3.1. Обобщенная структурная схема стеганографической системы при активном противодействии нарушителя

Пусть контейнер есть последовательность 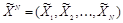с N независимо и идентично распределенными отсчетами в соответствии с p( ).

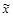Секретный ключ 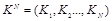доступен кодеру и декодеру стегосистемы. Каждый символ ключа K_i независимо и равновероятно распределен по функции p(K). По признаку наличия секретного ключа стегосистемы напоминают криптографические системы. Например, в системах шифрования секретный ключ предназначен для исключения возможности чтения нарушителем защищаемого сообщения. В отличие от криптографических систем, основной целью использования секретного ключа в рассматриваемых стегосистемах является обеспечение неопределенности для нарушителя распределения скрываемого сообщения в контейнере. Заметим, что в криптографии ключ и защищаемые сообщения должны быть взаимно независимы. Напротив, в ряде задач информационного скрытия полезно допускать зависимость между контейнером и ключом. Опишем эти зависимости, используя совместное распределение p( 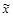,k). Пример таких зависимостей возникает, когда контейнерные данные доступны декодеру, что используется в ряде систем ЦВЗ [9,10]. В этом случае контейнер 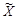может рассматриваться как часть секретного ключа. В других стегосистемах в качестве секретной ключевой информации могут использоваться выбранные отправителем хэш-функции [11], правило размещения водяных знаков в контейнере [12,13] или исходные данные для формирования псевдослучайных последовательностей в системах с расширением спектра контейнера [4,14].

В рассматриваемой обобщенной схеме стегосистемы скрываемые сообщения М равномерно распределены во множестве сообщений М и должны быть безошибочно переданы декодеру. Скрывающий информацию подает пустой контейнер 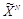, ключ 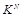и сообщение М на вход стегокодера, формируя стегограмму , передаваемую получателю по незащищенному каналу связи. Стего перехватывается и обрабатывается нарушителем с целью разрушения или удаления сообщения М. Искаженное нарушителем стего обозначим 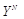и опишем атакующее воздействие условной функцией распределения 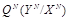. Эта обработка включает, как частный случай, формирование искаженного стего в виде 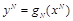, где 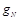есть детерминированное отображение.

Нарушителю полезно знать описание стегосистемы, используемой скрывающим информацию, и использовать это знание для построения более эффективного атакующего воздействия 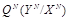. В частности, если известная нарушителю система информационного скрытия не использует секретного ключа 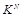, нарушитель способен декодировать сообщение М и затем удалить его из стего . Поэтому необходимо хранить описание бесключевой стегосистемы в секрете. Заметим, что история развития систем защиты информации, в частности, криптографических систем, свидетельствует, что не стоит надеяться на сохранение в тайне принципов построения системы защиты при ее широком применении. Поэтому нашим основным предположением является: нарушитель знает распределения всех переменных в стегосистеме и само описание стегосистемы, но не знает используемого секретного ключа (принцип Керкхофа для систем защиты информации).

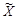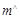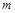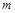
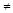
Пусть контейнер , стего X и модифицированное нарушителем стего Y принадлежат одному и тому же множеству X. Декодер получателя вычисляет оценку исходного скрываемого сообщения . Если 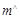, то атакующий сумел разрушить защищаемую стегосистемой информацию.

Рассмотрим часто используемую схему построения системы ЦВЗ, представленную на рис. 3.2. В данной схеме учитывается, что сообщение M обычно не принадлежит алфавиту X и имеет длину отличную от длины контейнера 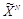. Например, если ЦВЗ представляет собой изображение фирменного знака производителя информационной продукции, то такой водяной знак по форме представления и по своим характеристикам существенно отличается от заверяемого контейнера. Поэтому скрываемое сообщение (ЦВЗ) M преобразуется в кодовую последовательность 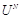длиной N символов, 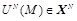. Эта операция преобразует водяной знак M к виду, удобному для встраивания в контейнер 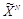. Заметим, что на рис. 3.2 показан случай, когда это преобразование независимо от контейнерного сигнала.

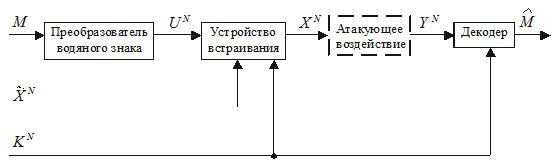
Рис. 3.2. Структурная схема стегосистемы водяного знака при активном противодействии нарушителя

Заверенное водяным знаком стего в общем случае формируется по правилу 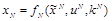, где 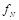есть функция встраивания по ключу 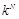. В обозначении функции встраивания неявно указывается, что она выполняет преобразования над блоком длины N. В простейшем примере встраивание может выполняться по правилу 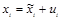для 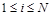, где переменные 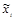, 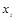и 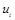принадлежат конечному алфавиту 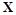. В современных системах водяного знака применяются сложные построения функции 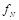, учитывающие характеристики чувствительности органов зрения или слуха человека и не являющиеся аддитивными [15]. Преобразование 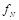должно быть удобным для скрывающего информацию, а также должно минимизировать вносимые искажения в контейнер при условии обеспечения требуемой устойчивости к атакам нарушителя. Оптимальное построение таких функций представляет сложную задачу.

Формально определим вносимые искажения в стратегиях скрывающего информацию и нарушителя. Это завершает математическое описание стегосистемы и позволяет определить скорость безошибочной передачи для стегосистемы, представленной на рис. 3.1.

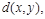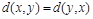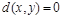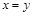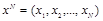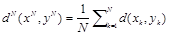Пусть искажения в стегосистеме оцениваются в соответствии с ограниченной неотрицательной функцией вида где . Используемая мера искажения симметрична: , выполнение равенства означает совпадение . Следовательно, используемая мера искажения является метрикой. Метрика искажений расширяется на последовательности длиной N символов и следующим образом: . Теория информационного скрытия использует классические метрики искажения, такие как метрики Хэмминга и Евклида, а также метрики, учитывающие особенности слуховой или зрительной чувствительности человека [16].

Назовем искажение контейнера 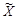, вызванное встраиванием в него скрываемого сообщения 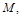искажением кодирования.

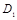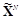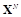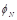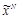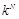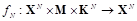
Определение 3.1: Стегосистема с длиной блока N, приводящая к искажению кодирования не более , есть совокупность множеств скрываемых сообщений M, контейнеров , стего и ключей и определенных на них функций кодирования f_N и декодирования , где есть отображение контейнера , сообщения m и ключа в стего 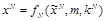. Это отображение ограничено величиной среднего искажения кодирования :

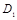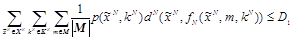; (3.1)

а 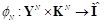есть декодирующее отображение принятой стегопоследовательности 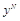и ключа 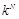в декодированное сообщение

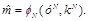
Таким образом, величина 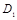характеризует искажение контейнера, максимально допустимое при встраивании в него скрываемого сообщения. Данное определение, хотя формально описывает стегосистемы блочного типа, может быть расширено и на стегосистемы поточного типа, у которых окно обработки описывается скользящим блоком длины N. В этом случае параметр N стегосистемы по аналогии с непрерывными кодами может быть назван длиной кодового ограничения стегосистемы.

Обычно искажение 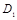мало, так как встраиваемое в контейнер сообщение должно быть незаметным для нарушителя. В стегосистемах, в которых контейнер представляет полезный для получателя информационный сигнал, величина 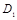ограничивается отправителем сообщений для сохранения высокого качества контейнера. В системах ЦВЗ требование минимизации 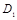формулируется как требование прозрачности водяного знака, заверяющего контейнер.

Заметим, что данное определение искажения использует усреднение относительно распределения 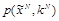и относительно равномерного распределения сообщений. Это позволяет воспользоваться классическими методами теории информации, сформулированными К. Шенноном [1]. Также возможно, но более сложно использовать для анализа стегосистем максимальное искажение контейнеров, где максимум отыскивается для распределений 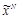, 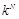и m.

Распределения 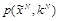, p(m) и выбор отображения fN определяют конкретный вид распределения 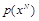множества формируемых стегограмм.

Определение 3.2: Атакующее воздействие без памяти, приводящее к искажению D₂, описывается условной функцией распределения 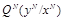из множества 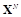во множество 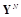, такой что

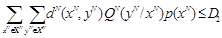. (3.2)

По определению 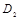есть максимальная величина искажения стегограммы, вызванное преднамеренными действиями нарушителя. Физический смысл ограничения величины 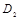заключается в следующем. В системах ЦВЗ нарушитель, пытаясь удалить водяной знак из заверенного контейнера, вынужден сам уменьшать величину 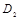, чтобы не исказить ценный для него контейнер. В других стегосистемах величина 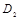ограничивается имеющимся у атакующего энергетическим потенциалом постановки помех, возникающими помехами для других каналов связи при использовании совместного ресурса и другими причинами.

Резонно предположить, что для реальных стегосистем обычно выполняется соотношение D₂ => D₁.

В соответствии с определением 3.2 атакующее воздействие описывается и ограничивается усредненными искажениями между множествам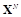и и 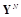. В других случаях, если атакующий знает описание функции f_N, то атакующее воздействие описывается и ограничивается усредненным искажением между множествам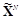и и :

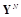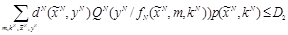. (3.3)

Определение D₂ в соответствии с выражением (3.3) предполагает, что нарушителю известны точные вероятностные характеристики контейнеров. Как будет показано далее, это обстоятельство существенно усложняет задачу обеспечения защищенности скрываемой информации, поэтому в стойких стегосистемах используются различные методы скрытия от нарушителя характеристик используемых контейнеров. Например, такие методы включают использование для встраивания подмножества контейнеров с вероятностными характеристиками, отличающимися от характеристик всего известного нарушителю множества контейнеров или рандомизированное сжатие контейнерного сигнала при встраивании в него скрываемого сообщения [17]. Поэтому вычисление искажения D₂ в соответствии с определением 3.2 является более универсальным, так как нарушитель всегда имеет возможность изучать вероятностные характеристики наблюдаемых стего.

Имея описание стегосистемы и атакующего воздействия 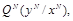можно описать состязание (игру) между скрывающим информацию и атакующим.

Определение 3.3: Информационно-скрывающее противоборство, приводящее к искажениям (D₁,D₂), описывается взаимодействием используемой стегосистемы, приводящей к искажению кодирования D₁, и атакующего воздействия, приводящего к искажению D₂.

Скорость передачи скрываемых сообщений по стегоканалу определим в виде R=1/N log 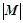. Скорость передачи R выражается в среднем числе бит скрываемых сообщений, безошибочно передаваемых (переносимых) одним символом (отсчетом) стегопоследовательности x^N. Это определение созвучно «классическому» определению скорости передачи обычных сообщений по каналу передачи, выражаемой в среднем числе безошибочно передаваемых бит за одно использование канала [1].

Вероятность разрушения скрываемого сообщения в стегопоследовательности длины N определим как

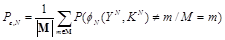, (3.4)

где скрываемые сообщения М равновероятно выбираются среди множества M. Вероятность 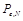есть средняя вероятность того, что атакующий успешно исказит скрытно передаваемое сообщение, усредненная над множеством всех сообщений. Атакующий добивается успеха в информационном противоборстве, если декодированное на приеме сообщение не совпадет с встроенным в контейнер скрываемым сообщением, или декодер не способен принять однозначного решения.

Теоретически достижимую скорость безошибочной передачи скрываемых сообщений и скрытую пропускную способность при искажениях не более величин (D₁, D₂) определим следующим образом.

Определение 3.4: Скорость R безошибочной передачи скрываемых сообщений достижима для искажений не более (D₁, D₂), если существует стегосистема с длиной блока N, приводящая к искажению кодирования не более D₁ на скорости R_N > R, такая что Р_e,N ? 0 при N ? ? при любых атаках нарушителя, приводящих к искажению не более D₂.

Определение 3.5: Скрытая пропускная способность С(D₁, D₂) есть супремум (верхняя грань) всех достижимых скоростей безошибочной передачи скрываемых сообщений при искажениях не более (D₁, D₂).

Отметим, что введенные определения средних искажений контейнеров при встраивании скрываемых сообщений и при атакующем воздействии нарушителя, скорости передачи скрываемых сообщений и пропускной способности канала скрытой передачи соответствуют теоретико-информационному подходу К. Шеннона.

Таким образом, скрытая ПС есть верхний предел скорости безошибочной передачи скрываемых сообщений, при которой искажения контейнера, вызванные вложением в него данных сообщений и действиями нарушителя по разрушению этих сообщений, не превышают заданных величин. Как и ПС каналов передачи открытых сообщений, ПС каналов передачи скрываемых сообщений определяется в идеализированных условиях, в которых задержка кодирования/декодирования бесконечна (N ? ?), статистика контейнеров, скрываемых сообщений, стего и ключей точно известна, сложность построения стегосистемы неограничена. Очевидно, что такая скрытая ПС имеет смысл теоретического предела, указывающего области, в которых существуют и, соответственно, не существуют стегосистемы при заданных величинах искажений. Известно, что скорости реальных систем передачи открытых сообщений могут только приближаться к величине ПС открытых каналов, причем по мере приближения к ней вычислительная сложность реализации систем передачи растет сначала приблизительно по линейной, затем по квадратической и далее по экспоненциальной зависимости от длины блока кодирования N [1]. По всей вероятности, аналогичные зависимости роста сложности справедливы и для стегосистем по мере приближения скорости передачи скрываемых сообщений к величине скрытой ПС. Это предположение подтверждается имеющимся опытом построения стегосистем. Известно, что попытки увеличить скорость передачи скрываемых сообщений влекут за собой существенное усложнение методов скрытия информации [6,8].

Подчеркнем абсолютный характер величины скрытой ПС для произвольного передачи скрываемой информации. Если требуемая скорость передачи скрываемых сообщений меньше величины скрытой ПС, то обеспечение безошибочной передачи в принципе возможно, и имеет смысл разрабатывать принципы построения реализующей эту скрытую ПС стегосистему. Если это соотношение не выполняется, то безошибочная передача невозможна при любых принципах построения стегосистем.

Данный текст является ознакомительным фрагментом.