3.3. Скрытая пропускная способность противника при активном противодействии нарушителя

3.3. Скрытая пропускная способность противника при активном противодействии нарушителя

3.3.1. Основная теорема информационного скрытия при активном противодействии нарушителя

Исследуем скрытую ПС при активном противодействии нарушителя, стремящегося разрушить скрытно передаваемую информацию. Информационно-скрывающее противоборство между отправителем сообщений и атакующим удобно описать методами теории игр. Цена игры равна величине скрытой ПС. Для максимизации скрытой ПС (максимизации платежа) скрывающий информацию оптимально строит скрывающее преобразование. Для минимизации скрытой ПС (минимизации платежа) атакующий синтезирует оптимальное атакующее воздействие. Величина скрытой ПС может быть получена последовательным соединением скрывающего преобразования и атакующего воздействия. Оценим величину скрытой ПС для стегосистемы с двоичным алфавитом. Исследуем теоретико-игровые аспекты проблемы скрытия информации стегосистемами.

Рассмотрим теорему, которая названа в [2] основной теоремой информационного скрытия при активном противодействии нарушителя. Для любых произвольно сложных стегосистем и любых атак без памяти эта теорема ограничивает сверху скорость безошибочной передачи для скрывающего информацию при условии, что атакующий знает описание скрывающего преобразования, а декодер знает описание и скрывающего преобразования и атакующего воздействия. Данное условие на самом деле не является трудновыполнимым, как это кажется на первый взгляд. Даже если стратегии действий скрывающего информацию и атакующего неизвестны, но стационарны, то можно утверждать, что и атакующий и декодер потенциально способны определить их, обработав достаточно большой объем статистического материала. Это допущение вполне реалистично, хотя и не всегда может быть достигнуто на практике из-за высокой вычислительной сложности.

Предварительно рассмотрим два утверждения, устанавливающие области существования стегосистем, потенциально способных безошибочно передавать скрываемую информацию при заданном атакующем воздействии.

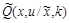Утверждение 3.1: Зафиксируем атакующее воздействия и выберем скрывающее преобразование , которое максимизирует количество информации вида

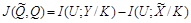(3.8)

над . Для любого сколь угодно малого значения ? > 0 и достаточно большого значения N существует стегосистема с длиной блока N, обеспечивающая вероятность разрушения скрываемых сообщений 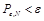для множества скрываемых сообщений мощностью .

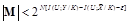Утверждение 3.2: Пусть стегосистема с длиной блока N способна безошибочно передавать скрываемые сообщения со скоростью 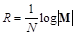при атакующем воздействии Q(y/x). Если для любого ? > 0 стегосистема обеспечивает вероятность 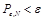при 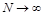, то существует конечный алфавит и такое скрывающее преобразование 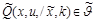, что выполняется .

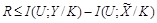Эти утверждения очень напоминают известные теоремы теории передачи сообщений в каналах связи с помехами [1].

Теорема 3.3: Пусть атакующий знает описание обобщенного скрывающего преобразования , а декодер знает описание обобщенного скрывающего преобразования и обобщенного атакующего воздействия . Для любого информационно-скрывающего противоборства, приводящего к искажениям не более (D₁, D₂), скорость передачи R скрываемых сообщений достижима, если и только если R < 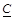, величина 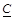определяется как

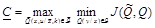, (3.9)

где U есть случайная переменная над произвольным конечным алфавитом U, переменные 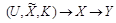образуют марковскую цепь, и количество информации 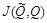определяется выражением (3.8).

Таким образом, теорема 3.3 определяет величину нижней грани скрытой ПС в условиях, когда все участники информационного противоборства знают стратегии действий друг друга. Заметим, что в этой теореме определяется величина скрытой ПС стегоканала, существование которого атакующему известно. Данная скрытая ПС равна среднему количеству информации на один элемент контейнера, которое нарушитель не может разрушить, выбирая любую стратегию противодействия из множества при искажении контейнера не более величины D₂.

Доказательство этой теоремы сводится к следующему: зафиксируем атакующее воздействие 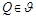. В утверждении 3.1 доказывается, что все скорости безошибочной передачи скрываемых сообщений менее 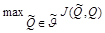достижимы. Утверждение 3.2 включает обратный результат, то есть достоверная передача невозможна выше этой скорости. Так как атакующий знает распределение , он способен выбрать такое распределение Q, которое минимизирует скорость передачи.

Следствие 3.4 далее показывает, что в важном специальном случае 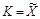(секретным ключом стегосистемы является описание используемого контейнера и сам контейнер известен декодеру), нет потери в оптимальности при ограничении кодера стегосистемы видом, представленным на рис. 3.2.

Следствие 3.4: В случае 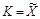, выбор значения переменной U оптимален, если и только если стего X может быть записано в форме 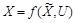, где отображение 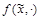обратимо для всех значений . В частности, выбор U = X оптимален. Скрытая ПС в этом случае определяется в виде

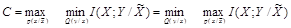. (3.10)

Это следует из того, что когда 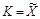, выражение (3.8) может быть записано в виде

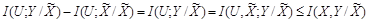. (3.11)

Представляется вполне логичным, что величина скрытой ПС равна взаимной информации между стего X и искаженным стего Y при условии, что отправителю и получателю скрываемой информации известен пустой контейнер .

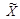Для практических систем защиты информации, если секретным ключом стегосистемы является описание используемого контейнера, возникают две проблемы. Во-первых, получатель должен знать исходный контейнер, что ограничивает возможную область применения таких стегосистем. Во-вторых, отправитель и получатель скрываемых сообщений должны использовать секретную ключевую информацию очень большого объема, что неудобно на практике.