3.12. Скрытая пропускная способность стегоканала при пассивном нарушителе

3.12. Скрытая пропускная способность стегоканала при пассивном нарушителе

В ранее рассмотренном подходе к определению скрытой ПС не рассматривается зависимость между ее величиной и характеристиками скрытности вложенных в контейнер сообщений. Это, в частности, объясняется тем, что в ряде стегосистем, таких как системы ЦВЗ или системы с идентификационными номерами, факт наличия аутентифицирующей информации в контейнере может и не скрываться от нарушителя. Соответственно, необнаруживаемость водяного знака нужна только с целью минимизации искажений контейнера с целью сохранения высокого качества заверяемых музыкальных, изобразительных или иных контейнеров, а также с целью затруднения оценки нарушителем эффективности действий по удалению (разрушению) водяного знака. Иная ситуация в стегосистемах, в которых способность нарушителя выявлять факт передачи скрываемых сообщений классифицируется как взлом системы.

Исследуем величину скрытой ПС стегоканалов, предназначенных для скрытой передачи информации. Противоборствующая сторона представлена пассивным нарушителем, пытающимся установить факт применения стегосистемы. В этой задаче информационного скрытия нарушитель не оказывает на стего мешающего воздействия, следовательно, к рассматриваемой стегосистеме не предъявляются требования по обеспечению устойчивости к преднамеренному разрушению скрываемых сообщений. Также будем считать, что в процессе передачи стего на него не воздействуют непреднамеренные помехи, следовательно, .

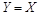Под скрытой ПС в рассматриваемых стегосистемах понимается максимальное количество информации, которое необнаруживаемым для нарушителя способом потенциально можно встроить в один элемент контейнера и затем извлечь без ошибок. В качестве элементов контейнера могут рассматриваться отсчеты звукового или речевого сигнала, дискретизированные в соответствии с теоремой Котельникова, или пикселы подвижного или неподвижного изображения.

Очевидно, что требования по повышению скрытой ПС, необнаруживаемости и устойчивости к удалению и разрушению являются взаимно противоречивыми, улучшить одну характеристику можно только за счет ухудшения других. Поэтому для систем ЦВЗ максимизируется устойчивость к удалению и разрушению водяного знака (максимизируется допустимое искажение D₂) при обеспечении сравнительно небольшой пропускной способности и достаточной незаметности, характеризуемой максимально допустимой величиной искажения кодирования D₁. В рассматриваемом классе информационно-скрывающих систем максимизируется скрытая пропускная способность при обеспечении требуемой необнаруживаемости стегоканала, а к помехоустойчивости предъявляются минимальные требования. Под необнаруживаемостью понимается способность стегосистемы скрывать факт передачи защищаемой информации от нарушителя.

В ряде работ [3, 4] величина скрытой ПС стегоканала определяется двумя факторами. Во-первых, аналогично тому, как в теории связи рассматривается передача сигналов по каналу связи, скрытая связь рассматривается как передача скрываемых сообщений по каналу с помехами. В качестве помехи рассматривается контейнерный сигнал. Это позволяет свести задачу передачи скрываемых сообщений к хорошо исследованной задаче передачи открытых сообщений по обычному каналу с помехами. В этой задаче отношение мощности скрываемого сигнала к мощности шума характеризует максимально достижимую скорость передачи скрываемой информации. В теории открытой связи целесообразно неограниченно увеличивать отношение сигнал/шум, чтобы максимизировать величину пропускной способности канала. В стеганографии, напротив, это отношение необходимо существенно ограничивать из-за действия второго фактора, заключающегося в необходимости обеспечения необнаруживаемости факта скрытой связи. При сопоставимых мощностях скрываемого сигнала и шума квалифицированным нарушителем легко выявляется факт наличия стегоканала. Следовательно, в стегосистемах приходится прятать скрываемый сигнал под значительно большим по величине шумом прикрытия. Поэтому, с одной стороны, для повышения скрытой ПС стегоканала необходимо увеличивать отношение сигнал/шум, а с другой стороны, для повышения защищенности стегоканала от его обнаружения необходимо это отношение существенно уменьшать. Следовательно, требуемый баланс может быть достигнут, если скрываемые сообщения безошибочно декодируются их законным получателем, но остаются необнаруживаемыми для нарушителя.

Заметим, что в соответствии с теорией оптимального приема если нарушитель и законный получатель скрываемых сигналов обладают одинаковой способностью по их обнаружению на фоне шумов контейнера, то величина скрытой ПС стегоканала равна нулю. Следовательно, для существования необнаруживаемого стегоканала нарушитель и получатель скрываемых сигналов должны находиться в неравных условиях. Канал передачи стегограмм для них равнодоступен, следовательно, получатель должен иметь преимущество в знании секретной информации, позволяющей ему выделить из смеси скрываемый сигнал+контейнер предназначенное для него сообщение, а нарушитель без знания этой информацию не должен быть способен отличить стего от пустого контейнера. Более подробно защищенность стегоканала от его обнаружения будет исследована в следующей главе.

В работе [4] для оценки скрытой пропускной способности аддитивного стегоканала используются оценки пропускной способности канала с аддитивным гауссовским шумом, описанным К. Шенноном в классической работе [1].

Пусть по каналу передается полезный сигнал с мощностью S, а в канале на него воздействует гауссовский шум Z с мощностью N. Выход аддитивного канала можно представить как 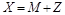. Упрощенная схема такой системы передачи представлена на рис. 3.12.

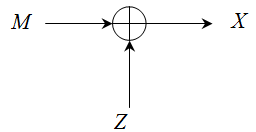
Рис. 3.12. Упрощенная схема стегоканала

Для оценки величины скрытой пропускной способности аддитивного стеганографического канала сопоставим ее с величиной пропускной способности канала с аддитивным белым гауссовским шумом. Если входной сигнал М и шум Z независимы, то условная энтропия выходного сигнала Х при заданном М равна энтропии шумового сигнала. Используем этот результат для определения пропускной способности аддитивного канала с шумом

.

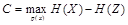Пусть шум Z имеет нормальное распределение со средним значением 0 и дисперсией N. Тогда энтропия Z равна

.

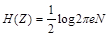Чтобы достичь максимума величины ПС по всем возможным распределениям входа, будем считать, что входной сигнал M имеет также нормальное распределение с дисперсией S. Следовательно, X есть сумма двух гауссовских сигналов и имеет дисперсию S + N. Тогда пропускная способность С_g гауссовского канала выражается, как

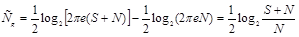. (3.29)

Из теории связи известно [25], что величина ПС канала минимальна, когда шум в канале гауссовский со средним значением 0. Следовательно, пропускная способность других аддитивных негауссовских каналов ограничивается снизу величиной С_g (3.29). Уравнения (3.30) — (3.32) определяют пропускные способности трех таких каналов с различными распределениями шума.

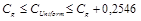, (3.30)

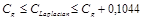, (3.31)

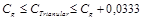. (3.32)

Рассмотрим стеганографическую систему, в которой скрываемая информация добавлена некоторым образом к контейнерным данным. Например, скрываемое сообщение записывается на место наименее значащих бит (НЗБ) яркости пикселов контейнерного изображения. Во многих практических стегосистемах скрываемое сообщение до встраивания шифруется или сжимается каким-либо архиватором данных. Это повышает скрытность связи и позволяет описать зашифрованное (сжатое) сообщение в виде последовательности с независимо и равновероятно распределенными битами.

Величину скрытой пропускной способности стегоканала оценим путем сравнения с пропускной способностью канала с белым гауссовским шумом. Однако в действительности сигналы реальных источников информации, таких как речь и видео, нельзя описать гауссовскими сигналами, потому что в их структуре высока зависимость между соседними отсчетами. Как и в других случаях негауссовских каналов, скрытая пропускная способность стегоканала, в котором скрываемые сообщения внедряются в негауссовские сигналы, ограничена снизу пропускной способностью канала с белым гауссовским шумом.

Неопределенность шума с произвольным распределением может быть сравнена с белым гауссовским шумом, используя измерение энтропийной мощности N_e. Если произвольный шум Z имеет энтропию Н(Z), то его средняя шумовая мощность равна мощности гауссовского шума, имеющего такую же энтропию и определяется как

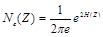. (3.33)

Объединяя (3.33) с оценкой пропускной способности канала с аддитивным шумом получим, что скрытая пропускная способность С стегоканала ограничена

.

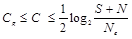где N_e — энтропийная мощность контейнера. Так как величина N_e строго меньше, чем N для всех негауссовских сигналов, то величина С_g является нижней границей для скрытой ПС стегоканалов, использующих произвольные контейнеры.

Верхняя граница скрытой ПС определяется максимумом взаимной информацией между скрываемым сообщением и стего, полагая, что стего имеет нормальное распределение с дисперсией S + N и шум в канале является гауссовским с мощностью N_e. Следовательно

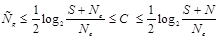. (3.34)

Очевидно, что если контейнер можно представить в виде белого гауссовского шума, то его энтропийная мощность уменьшается до величины N и скрытая ПС принимает минимальное значение, равное С_g.

Для аналитической оценки количества скрываемой информации в избыточных контейнерах, таких как изображения или речевые сигналы, необходимо знать их распределения вероятностей. Однако точные вероятностные характеристики таких контейнеров неизвестны и вряд ли когда-либо станут известными в силу нестационарности естественных источников контейнеров. Несмотря на это, можно воспользоваться известными результатами сжатия избыточных сигналов, чтобы оценить верхнюю границу энтропии источника сигналов. В ряде работ разрабатывались достаточно сложные алгоритмы сжатия, предназначенные для максимального удаления избыточности из сжимаемых сигналов [4,32]. Достигнутое в ходе работы таких алгоритмов среднее число бит на один символ сжимаемых сигналов может быть использовано как практическая верхняя граница энтропии исследуемого источника. Например, для изображений лучшим на сегодня алгоритмом сжатия без потерь CALIC [4] достигнута скорость 2,99 бит на пиксел. Эта оценка получена на 18 полутоновых тестовых изображениях, выбранных ISO (Международной организацией по стандартизации), яркость пикселов которых представлена 8 битами. Используя величину достигнутой алгоритмом CALIC скорости как оценку энтропии изображений, мы можем вычислить как верхнюю, так и нижнюю границы скрытой пропускной способности стегоканала, в котором скрываемая информация встраивается в изображение-контейнер. Из полученной оценки энтропии изображений по формуле (3.33) легко определить величину энтропийной мощности контейнеров.

В итоге средняя мощность среди тестовых изображений ISO и средняя скорость алгоритма CALIC были использованы для вычисления границ скрытой пропускной способности для широкого диапазона значений отношения мощности скрываемого сигнала к мощности контейнерного шумового сигнала. На рис. 3.13 пунктирной линией показана величина пропускной способности С_g канала с белым гауссовским шумом. Средняя скорость CALIC по всем изображениям равна 4,9588 бит на пиксел, а средняя мощность сигналов изображения — 2284,7. Сплошная линия на рисунке показывает верхнюю границу скрытой пропускной способности, прерывистая — нижнюю. При уменьшении отношения мощности скрываемого сигнала к мощности контейнерного шумового сигнала нижняя граница скрытой пропускной способности снижается до 0. Реальное значение скрытой пропускной способности стегоканала находится между верхней и нижней границами и отражает то количество скрываемой информации, которое можно внедрить в один пиксел усредненного контейнерного изображения.

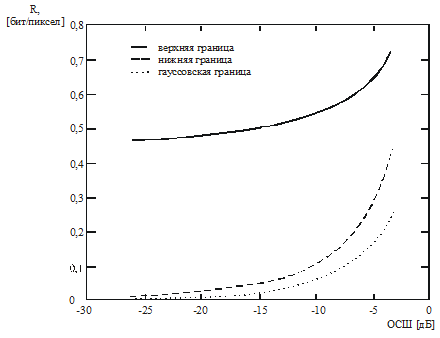
Рис. 3.13. Оценки скорости передачи скрываемых сообщений в зависимости от отношения сигнал/шум

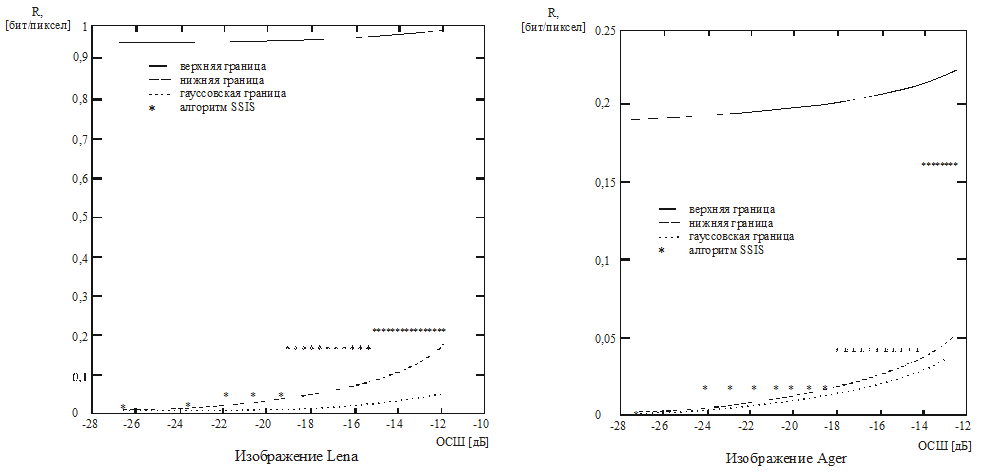
Рис. 3.14. Оценки скорости передачи скрываемых сообщений в зависимости от отношения сигнал/шум для низкочастотного изображения «Lena» и высокочастотного изображения «Eiger»

Верхние и нижние границы скрытой ПС в работе [4] были вычислены для двух типовых полутоновых изображений. На левом графике рис. 3.14 показаны верхняя и нижняя границы величины скрытой пропускной способности стеганографического канала для тестового портретного изображения «Lena». В качестве оценки энтропии этого изображения была использована достигнутая алгоритмом CALIC скорость 4,6321 бит на пиксел. Правый график показывает верхнюю и нижнюю границы величины скрытой ПС для тестового пейзажного изображения «Eiger» (скорость CALIC 5,2366 бит на пиксел). На этих же графиках точками указаны достигнутые скорости передачи скрываемого сообщения в предложенной в работе [4] системе скрытия данных в изображении с расширением спектра (SSIS). Отметим, что достигнутые в стегосистеме SSIS скорости передачи скрываемых сообщений лежат между верхней и нижней границами скрытой пропускной способности, вычисленных для использованных контейнерных изображений.

Из рис. 3.13 и рис. 3.14 видно, что величина скрытой ПС приблизительно линейно зависит от отношения сигнал/шум при малых величинах ОСШ. Отношение сигнал/шум может быть использовано в качестве объективной оценки степени необнаруживаемости скрываемого сообщения. Для различных видов скрываемых сообщений допустимая величина ОСШ разная. Пусть в аддитивной стегосистеме речевое сообщение скрытно передается в составе контейнера с гауссовским распределением. Признаки наличия речи не выявляются на слух и с использование инструментальных методов при ОСШ не превышающем -16…-20 дБ [33]. Если прятать речь в изображении, характеристики которого существенно отличаются от статистики гауссовского сигнала, то можно надеяться, что допустимая с точки зрения необнаруживаемости величина ОСШ может быть уменьшена. Это важно с точки зрения увеличения скрытой ПС. Например, при ОСШ равном -18 дБ, согласно описанным границам в низкочастотном изображении «Lena» можно скрыть не менее 0,05…0,95 бит речевой информации на пиксел изображения.

Пусть в аддитивной стегосистеме в изображение-контейнер внедряется скрываемое изображение. Различные изображения характеризуются большим разбросом корреляционных зависимостей между пикселами. Для скрытой передачи низкочастотных изображений, у которых корреляционные зависимости являются значительными (например, к этому классу относится портретное изображение «Lena»), требуемое отношение мощности скрываемого изображения к мощности гауссовского контейнера должно быть не более -20…-25 дБ. Для высокочастотных изображений типа пейзаж, надежное скрытие может быть обеспечено при большем значении ОСШ, порядка -10…-15 дБ. Таким образом, проще прятать изображения с большим количеством мелких деталей в гауссовском контейнере. Заметим, что эти цифры являются ориентировочными и справедливы для контейнеров с нормальным распределением. При скрытии изображения в изображении, допустимая величина ОСШ может быть уменьшена. Таким образом, в зависимости от характера скрываемого и контейнерного изображения в каждом пикселе контейнерного изображения потенциально можно надежно прятать от 0,01 до 1 бита графической информации.

Однако следует учитывать, что приведенные оценки скрытой ПС указывают на потенциальную возможность скрытия такого количества информации в усредненном элементе контейнера, но не гарантируют, что в реальных стегосистемах скорости передачи скрываемой информации будут близки к этим теоретическим оценкам и при этом будет обеспечиваться стойкость к произвольным методам стегоанализа. От излишнего оптимизма предостерегает крах многих предложенных к настоящему времени стегосистем, для которых очень быстро были разработаны эффективные методы стегоанализа. В частности, в следующей главе будет показано, как на основе визуальной и статистических атак уверенно обнаруживаются следы скрываемой информации при ее встраивании в наименее значащие биты элементов изображений и аудиосигналов. Необходимо отметить, что отношение сигнал-шум является характеристикой скрытия не более чем первого порядка при использовании методов стегоанализа, и потому для уверенности в надежном скрытии информации требуется использовать и другие оценки необнаруживаемости.

В работе [5] с позиций теории информации исследована скрытая пропускная способность стегоканала при следующей постановке. При передаче изображений широко используются алгоритмы сжатия типа JPEG, JPEG2000, MPEG, вносящие в изображение некоторую допустимую для получателя погрешность. Пусть 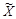есть контейнерное изображение, М — встраиваемое сообщение. После вложения сообщение М в контейнер 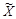сформированное стего подвергается сжатию с погрешностью. Будем полагать, что встраивание сообщения в контейнер, а также сжатие стего описываются отображениями при которых на скрываемое сообщение аддитивно воздействуют шум встраивания и, соответственно, шум сжатия. Это позволяет представить анализируемую стегосистему в виде, показанном на рис. 3.15.

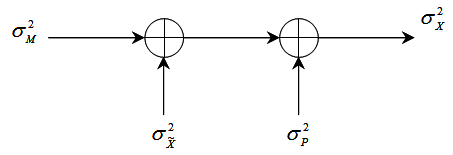
Рис. 3.15. Упрощенная схема аддитивной стегосистемы со сжатием стего

Обозначим мощность встраиваемого сигнала в виде 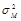, мощность контейнера — 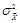, а мощность шума, добавляемого при сжатии через 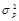. Предположим, что контейнер и шум сжатия имеют нормальное распределение. Тогда оба источника шума можно объединить в один источник Z с дисперсией 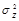= 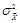+ 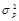. В соответствии с теорией связи, пропускная способность канала передачи сообщения М при воздействии независимого от него шума Z равна 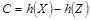. При фиксированных вероятностных характеристиках шума пропускная способность увеличивается максимизацией значения энтропии 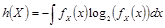выбором соответствующего распределения скрываемого сообщения. Известно [25], что величина 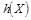максимальна при нормальном распределении :

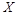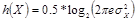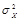, где есть дисперсия стего.

Соответственно, энтропия источника Z равна

.

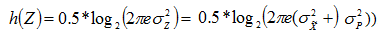Тогда скрытая пропускной способность рассматриваемого стегоканала равна

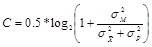. (3.35)

Отметим, что данная оценка величины скрытой ПС справедлива при условии, что распределения скрываемых сообщений, контейнера и шума сжатия описываются нормальным законом. Это условие не выполняется строго для реальных изображений и реальных алгоритмов их сжатия. Поэтому в работе [5] для вычисления величины скрытой ПС мощность изображений приводится к энтропийной мощности гауссовского сигнала, оказывающего на скрываемое сообщение такое же мешающее воздействие, что и реальное изображение.

Рассмотрим гауссовский контейнер, амплитуды отсчетов которого равномерно распределены в диапазоне значений от 0 до 255 с дисперсией 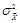. Энтропия равномерно распределенной величины определяется выражением 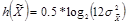бит. Отсюда 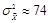. Однако, как исследовано в работе [5], для реальных изображений 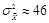, так как они обладают некоторой избыточностью.

Так как распределение шума сжатия в практически используемых алгоритмах обработки точно неизвестно, то на наихудший случай предположим, что шум сжатия гауссовский. Пусть при осуществлении вложения скрываемой информации в контейнер допускается искажение исходного изображения до величины пикового отношения сигнал/шум (ПОСШ) порядка 40 дБ. Такое искажение практически незаметно на глаз. Тогда допустимая мощность скрытого сообщения равна 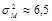. В работе [5] производилась оценка шума, возникающего при сжатии изображений алгоритмом JPEG с показателем качества 50 %. Из результатов экспериментов следует, что 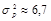. Тогда легко подсчитать, что величина скрытой пропускной способности составляет C = 0,0022 бит/пиксел, или 140 бит для изображения размером 256 ? 256 пикселов. Пиковое отношение сигнал/шум изображения при этом обеспечивается не менее 37 дБ. При сжатии изображений с более высоким коэффициентом сжатия мощность шума сжатия существенно возрастает. При 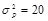величина C уменьшается до 0,0019 бит/пиксел, или 124 бита для того же изображения. При этом ПОСШ снижается и составляет не менее 34 дБ, что еще допустимо для большинства изображений. Заметим, что при увеличении шума сжатия задача нарушителя по обнаружению стегоканала существенно усложняется, так как задачу обнаружения скрываемых сообщений приходится решать при большем уровне маскирующего шума. Таким образом, при увеличении шума обработки при сжатии изображений величина скрытой пропускной способности уменьшается достаточно плавно, а защищенность, напротив, существенно повышается. Следовательно, вполне может быть использована обработка изображений по алгоритму JPEG с умеренным коэффициентом сжатия после встраивания в них скрываемых сообщений.

Данный текст является ознакомительным фрагментом.