5.3. Скрытие данных в области преобразования

5.3. Скрытие данных в области преобразования

5.3.1. Выбор преобразования для скрытия данных

В большинстве методов скрытия данных в изображениях используется та или иная декомпозиция изображения — контейнера. Среди всех линейных ортогональных преобразований наибольшую популярность в стеганографии получили вейвлет-преобразование и ДКП, что отчасти объясняется их успешным применением при сжатии изображений. Кроме того, желательно применять для скрытия данных то же преобразование изображения, как и то, котоорому оно подвергнется при возможном дальнейшем сжатии. В стандарте JPEG используется ДКП, а в JPEG2000 — вейвлет-преобразование. Стегоалгоритм может быть весьма робастным к дальнейшей компрессии изображения, если он будет учитывать особенности алгоритма сжатия. При этом, конечно стегоалгоритм, использующий ДКП, вовсе не обязательно будет робастным по отношению к вейвлетному алгоритму сжатию. Стегоалгоритм, использующий вейвлеты, может быть неробастным к сжатию с применением ДКП. Еще большие трудности с выбором преобразования при скрытии данных в видеопоследовательности. Причина заключается в том, что при сжатии видео основную роль играет кодирование векторов компенсации движения, а не только неподвижного кадра. Робастный стегоалгоритм должен каким-то образом учитывать это.

Возникает следующий вопрос: существует ли робастное преобразование, независимое от применяемого далее алгоритма сжатия? В работе [15] с позиций теории информации рассмотрены различные ортонормальные преобразования, такие как ДПФ, ДКП, Хартли, субполосное преобразование.

Известно много моделей для оценки пропускной способности канала скрытия данных. Так, в работе [16] представлена следующая модель.

Пусть S₀ - исходное изображение (контейнер), W — вложение. Тогда модифицированное изображение 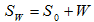. Модифицированное изображение визуально неотличимо от исходного и может быть подвергнуто сжатию с потерями: 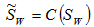, где C(.) — оператор компрессии. Биты вложения W должны быть извлечены из 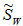. Вопрос: какое количество бит может быть вложено в данное изображение и извлечено из него с произвольно малой вероятностью ошибки, то есть какова пропускная способность канала скрытия данных, при данном алгоритме сжатия?

Блок-диаграмма рассматриваемого стегоканала представлена на рис. 5.8.

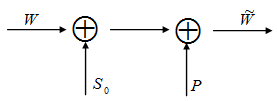
Рис. 5.8. Блок-диаграмма стегоканала

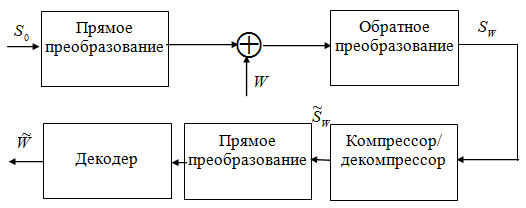
Рис. 5.9. Структурная схема стегосистемы

Сообщение W передается по каналу. Канал имеет два источника «шума»: S₀ - изображение-контейнер и P — «шум», возникающий при компрессии/декомпрессии. 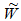- возможно искаженное сообщение.

Структурная схема схема стегосистемы приведена на рис. 5.9. Изображение декомпозируется на L субполос. К каждой субполосе «подмешивается» скрытая информация. После обратного преобразования получается модифицированное изображение S_w. После компрессии/декомпрессии получается изображение 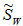. Оно подвергается прямому преобразованию, и из каждой из L субполос независимо извлекается скрытое сообщение.

Реальные изображения вовсе не являются случайным процессом с равномерно распределенными значениями величин. Хорошо известно, и это используется в алгоритмах сжатия, что большая часть энергии изображений сосредоточена в низкочастотной части спектра. Отсюда и потребность в осуществлении декомпозиции изображения на субполосы. Стегосообщение добавляется к субполосам изображения. Низкочастотные субполосы содержат подавляющую часть энергии изображения и, следовательно, носят шумовой характер. Высокочастотные субполосы наиболее подвержены воздействию со стороны различных алгоритмов обработки, будь то сжатие или НЧ фильтрация. Таким образом, для вложения сообщения наиболее подходящими кандидатами являются среднечастотные субполосы спектра изображения. Типичное распределение шума изображения и обработки по спектру частоты показано на рис. 5.10.

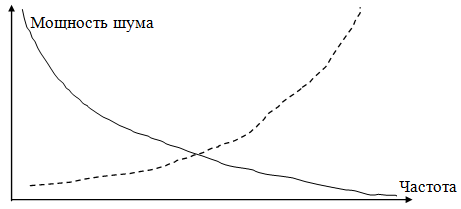
Рис. 5.10. Зависимость шума изображения (сплошная линия) и шума обработки (пунктирная линия) от частоты

Стегоканал можно декомпозировать на ряд независимых подканалов. Это разделение осуществляется за счет выполнения прямого и обратного преобразования. В каждом из L подканалов имеется по два источника шума. Пусть 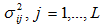— дисперсия коэффициентов преобразования (шума изображения) в каждом из подканалов. Тогда выражение для пропускной способности канала стегосистемы примет вид 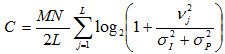, где ?_j — визуальный порог для j-й субполосы. Иными словами, ?²_j - максимально допустимая энергия стегосообщения, исходя из требований сохранения визуального качества изображения.

Шум обработки появляется в результате квантования коэффициентов трансформанты. Значение этого шума легко получить, скажем, для пары ДКП — JPEG, если известны таблицы квантования. Однако, например, в случае преобразования Адамара один коэффициент ДКП будет влиять на несколько коэффициентов Адамара. Хотелось бы иметь более общее определение шума обработки. Его можно рассматривать как уменьшение корреляции между коэффициентами трансформанты исходного изображения и квантованными коэффициентами. Например, при высоких степенях сжатия может возникнуть ситуация, когда будут отброшены целые субполосы. То есть дисперсия шума в этих субполосах, вообще говоря, бесконечна. Налицо уменьшение корреляции между коэффициентами субполосы до квантования и после. Конечно для получения приемлемых результатов необходимо усреднить значение шума обработки по многим изображениям.

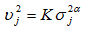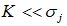Выбор значения визуального порога основывается на учете свойств СЧЗ. Известно, что шум в ВЧ областях изображения более приемлем, чем в НЧ областях. Можно ввести некоторые взвешивающие коэффициенты, , где и 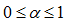. Случаю ? = 0 соответствует равномерное распределение стего по всем субполосам, случаю ? = 1 соответствует распределение стего в соответствии с дисперсиями субполос. После некоторых упрощений можно получить выражение для пропускной способности: 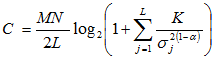. Как видно из этого выражения, при ? = 1 декомпозиция никак не будет влиять на пропускную способность стегоканала. При ? < 1 это не так. Таким образом, пропускная способность возрастает за счет того, что в области с низкой дисперсией (высокочастотные) добавляется относительно больше энергии стегосигнала.

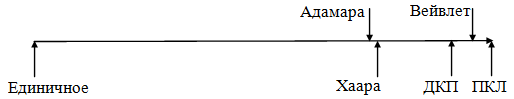
Рис. 5.11. Различные преобразования, упорядоченные по достигаемым выигрышам от кодирования

В работе [15] были произведены многочисленные эксперименты, которые позволили дать определенные рекомендации по выбору преобразования для стеганографии. Известно, что преобразования можно упорядочить по достигаемым выигрышам от кодирования (см. рис. 5.11). Под выигрышем от кодирования понимается степень перераспределения дисперсий коэффициентов преобразования.

Наибольший выигрыш дает преобразование Карунена-Лоэва (ПКЛ), наименьший — разложение по базису единичного импульса (то есть отсутствие преобразования). Преобразования, имеющие высокие значения выигрыша от кодирования, такие как ДКП, вейвлет-преобразование, характеризуются резко неравномерным распределением дисперсий коэффициентов субполос. Высокочастотные субполосы не подходят для вложения из-за большого шума обработки, а низкочастотные — из-за высокого шума изображения. Поэтому приходится ограничиваться среднечастотными полосами, в которых шум изображения примерно равен шуму обработки. Так как таких полос немного, то пропускная способность стегоканала невелика. В случае применения преобразования с более низким выигрышем от кодирования, например, Адамара или Фурье, имеется больше блоков, в которых шум изображения примерно равен шуму обработки. Следовательно, и пропускная способность выше. Неожиданный вывод: для повышения пропускной способности стеганографического канала лучше применять преобразования с меньшими выигрышами от кодирования, плохо подходящие для сжатия сигналов.

Эффективность применения вейвлет-преобразования и ДКП для сжатия изображений объясняется тем, что они хорошо моделируют процесс обработки изображения в СЧЗ, отделяют «значимые» детали от «незначимых». Значит, их более целесообразно применять в случае активного нарушителя. В самом деле, модификация значимых коэффициентов может привести к неприемлемому искажению изображения. При применении преобразования с низкими значениями выигрыша от кодирования существует опасность нарушения вложения, так как коэффициенты преобразования менее чувствительны к модификациям. Однако, существует большая гибкость в выборе преобразования. И если преобразование неизвестно нарушителю (хотя учет этого момента и противоречит принципу Керхгофа), то модификация стего будет затруднена.

Данный текст является ознакомительным фрагментом.