9. Закон распределения Пуассона и Гаусса

9. Закон распределения Пуассона и Гаусса

Закон Пуассона. Другое название его – закон ра-определения редких событий. Закон Пуассона (З. П.) применяется в тех случаях, когда маловероятно, и поэтому применение Б/З/Р нецелесообразно.

Достоинствами закона являются: удобство при вычислении, возможность вычислить вероятность в заданном промежутке времени, возможность замены времени другой непрерывной величиной, например, линейными размерами.

Закон Пуассона имеет следующий вид:

и читается следующим образом: вероятность появления события А в m раз при n независимых испытаниях выражается формулой вида (59), где а = пр – среднее значение p(A), причем а является единственным параметром в законе Пуассона.

Закон нормального распределения (закон Гаусса). Практика неуклонно подтверждает, что закону Гаусса с достаточным приближением подчиняются законы распределения ошибок при измерениях самых различных параметров: от линейных и угловых размеров до характеристик основных механических свойств стали.

Плотность вероятности закона нормального распределения (в дальнейшем Н. Р.) имеет вид

где x₀ – среднее значение случайной величины;

? – среднее квадратическое отклонение той же случайной величины;

e = 2,1783… – основание натурального логарифма;

Ж – параметр, который удовлетворяет условию.

Причина широкого применения закона нормального распределения теоретически определяется теоремой Ляпунова.

При известных Х₀ и ? ординаты кривой функции f(x) можно вычислить по формуле

где t – нормированная переменная,

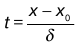
(t) плотность вероятности z. Если подставить z и (t) в формулу, то следует:

Кривую З.Н.Р. часто называют кривой Гаусса, этот закон описывает очень многие явления в природе.