Глава 1 Цифровое представление

Как для компьютера, так и для микроконтроллера окружающий мир представляется в виде различных чисел. В десятичной системе счисления числовые величины описываются с помощью десяти цифр: 0, 1…., 9. Используя при необходимости символы «+», «—» и «.»[6], можно выразить любое число из диапазона . На самом деле, с помощью чисел можно выражать даже нечисловые понятия. К примеру, в коде ASCII (американский стандартный код обмена информацией) символу «А» соответствует число 65, символу «В» — 66…., «Z» — 90, «а» — 97, «Ь» — 98…., «z» — 122 и т. д. Соответственно, слово «Microcontroller» можно закодировать в виде последовательности чисел «77, 105, 99, 114, 111, 99, 111, 110, 116, 114, 111, 108, 108, 101, 114». При условии, что нам известен контекст, т. е. какие числа описывают реальные числовые величины, а какие — текст, с их помощью можно закодировать практически любые символы[7].

Электронные схемы не очень хорошо подходят для хранения и обработки множества различных значений. Да, первая американская цифровая вычислительная машина ENIAC (электронный цифровой интегратор и калькулятор), созданная в 1964 году, выполняла арифметические операции в десятичном виде[8], однако все компьютеры, появившиеся впоследствии, оперировали уже данными в двоичной (с основанием 2) системе. В действительности десятичная система счисления удобна только для человека, поскольку у нас на руках 10 пальцев[9]. Так что в этой главе мы будем рассматривать исключительно свойства двоичных разрядов, их группирование, а также операции над двоичными числами. Прочитав главу, вы:

• Поймете, почему двоичное представление данных является наиболее удобным для цифровых схем.

• Узнаете, как одну и ту же величину можно выразить в двоичном, шестнадцатеричном и двоично-десятичном (BCD) виде.

• Научитесь выполнять сложение и вычитание двоичных чисел.

• Узнаете, как выполнять умножение посредством сдвига влево.

• Узнаете, как выполнять деление посредством сдвига вправо с копированием знакового бита.

• Познакомитесь с логическими операциями НЕ, И, ИЛИ и Исключающее ИЛИ.

В основе информационных технологий лежит обработка, вычисление и передача информации, представленной в цифровом виде. Эта информация в подавляющем большинстве случаев представлена в виде множества двоичных разрядов (битов[10])). Как правило, такая обработка осуществляется с использованием микропроцессоров[11] и микроконтроллеров. Интересно отметить, что вычислительная мощность современной звуковой открытки превышает совокупную мощность всех вычислительных устройств, имевшихся на планете в 1950 году!

Двоичная система — это универсальный способ представления данных, поскольку простейшим устройством, которое можно реализовать на одном транзисторе, является электронный ключ. Такие ключи, имеющие только два состояния, очень малы; они способны очень быстро изменять свое состояние и потребляют незначительный ток. Более того, поскольку требуется различать только два состояния, очевидно, что двоичное представление менее подвержено воздействию помех. Из сказанного становится ясно, что и плотность компоновки элементов на кристалле, и скорости переключения этих элементов могут достигать очень больших значений. Хотя сам ключ как таковой не обладает какой-либо вычислительной мощностью, 5 миллионов ключей, переключающихся 100 миллионов раз в секунду, способны продемонстрировать, по крайней мере, видимость интеллекта!

Два состояния бита обычно называются логическим нулем (лог. 0) к логической единицей (лог. 1) или просто 0 и 1. Один бит может быть представлен двумя состояниями любой физической величины, например напряжения или силы электрического тока, освещенности, давления воздуха. В большинстве микроконтроллеров состоянию лог. 0 соответствует напряжение 0 В (или «земля»), а состоянию лог. 1 — напряжение +3…5 В, хотя это правило и не универсально. Например, в последовательном порту RS-232 вашего ПК для индикации состояния лог. 0 используется напряжение +12 В, а для индикации состояния лог. 1 — напряжение -12 В.

Итак, один бит может представлять только два состояния. Более сложные элементы можно выразить с помощью комбинаций битов. Например, обычные алфавитно-цифровые символы[12] можно представить с помощью 7-битных групп двоичных разрядов, как показано в Табл. 1.1. Таким образом, ASCII-представление строки «Microcontroller» будет иметь вид

1001101 1101001 1100011 1110010 1101111 1100011 1101111 1101110

1110100 1110010 1101111 1101100 1101100 1100101 1110010

В кодировке Юникод (Unicode), являющейся дальнейшим развитием кодировки ASCII, используются уже 16-битные группы, поэтому с ее помощью можно выразить символы всех существующих языков, а также различные математические и прочие специальные символы.

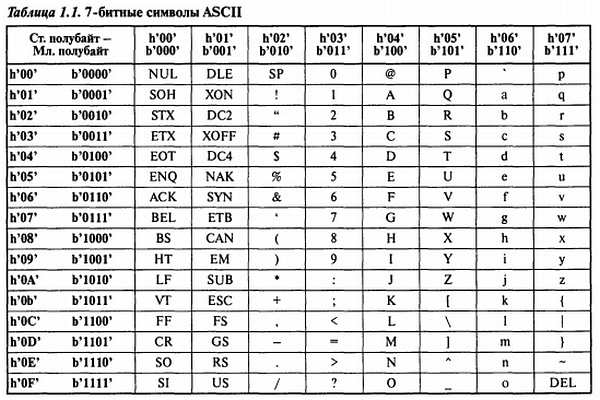
Код ASCII называется невзвешенным, поскольку отдельные биты не несут какого-либо смысла; значение имеет только вся совокупность битов. В качестве других примеров невзвешенных кодов можно отметить код значения на гранях игральной кости и семисегментный код, изображенный на Рис. 6.8 (стр. 183). Мы же в основном будем работать с обычным двоичным взвешенным кодом, в котором позиция бита определяет его величину или, иначе, вес. В целом двоичном числе самый правый бит имеет вес 2⁰ = 1, находящийся слева от него — 2¹ = 2 и так далее до n-й позиции, бит в которой имеет вес 2^n-1. В частности, десятичное число 1998 представляется таким образом:

10³ 10² 10¹ 10⁰

1     9    9    8

т. е. 1х10³ + 9х10² + 9х10¹ + 8х10⁰, или 1998. В обычном двоичном коде то же самое число представляется следующим образом:

2¹⁰ 2⁹ 2⁸ 2⁷ 2⁶ 2⁵ 2⁴ 2³ 2² 2¹ 2⁰

1   1   1   1   1   0   0  1  1  1  0

т. е. 1х2¹⁰ + 1х2⁹+ 1х2⁸ + 1х2⁷ + 1х2⁶ + 0х2⁵ + 0х2⁴ + 1х2³ + 1х2² + 1х2¹ + 0x2⁰, или b’111111001110’[13]. Точно так же можно представлять и дробные числа, при этом позициям, расположенным справа от десятичной точки, соответствуют отрицательные степени двойки. Так, двоичное число b’1101.11’ эквивалентно десятичному 13.75. Из примера видно, что двоичное представление чисел гораздо длиннее их десятичных эквивалентов — в среднем не менее чем в 3 раза. Однако 2-позиционный ключ гораздо проще 10-позиционного, поэтому двоичное представление предпочтительнее.

Биты любой n-разрядной двоичной последовательности могут образовывать в общей сложности 2ⁿ комбинаций. При этом большинство компьютеров хранят и обрабатывают биты группами. Например, первый микропроцессор Intel 4004 обрабатывал данные по четыре бита (полубайт) за раз. Большинство современных процессоров оперируют с 8-битными (байт), 16-битными (слово), 32-битными (двойное слово) и 64-битными (счетверенное слово) блоками. Характеристики некоторых из указанных групп перечислены в Табл. 1.2. Приведенные названия являются в какой-то мере стандартом де-факто, однако иногда встречаются и другие варианты.

Как и в десятичной системе счисления, большие двоичные числа часто выражаются с использованием приставок К (кило), М (мега) и Г (гига). В двоичной системе приставка «кило» соответствует множителю 2¹⁰, например 64 Кбайт (или КБ) памяти. Аналогично, приставка «мега» соответствует множителю 2²⁰= 1 048 576, например дискета объемом 1.44 Мбайт (или МБ). Точно так же емкость 20 Гбайт (или ГБ) винчестера составляет 20х2³⁰= 21 474 836 480 байт. Естественно, 1-й вариант записи предпочтительнее.

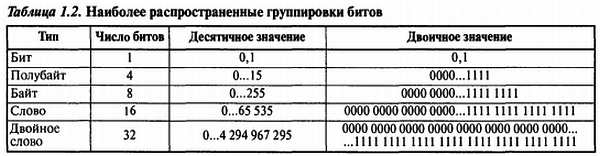
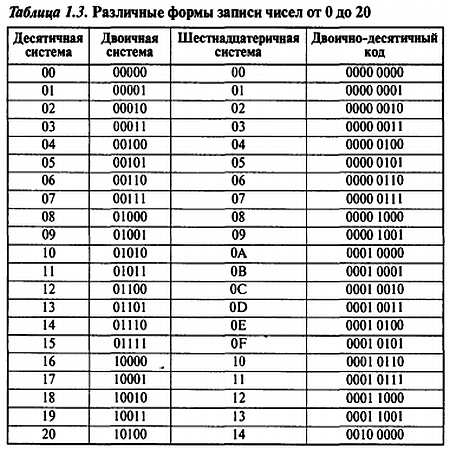
Длинные двоичные числа очень неудобны для человеческого восприятия. В Табл. 1.2 двоичные числа специально были разбиты на 4-битные группы, чтобы их удобнее было читать. Предположим теперь, что адрес какого-либо элемента в памяти равен Ь’1000 1100 0001 0100 0000 1010’. Если каждой комбинации из четырех битов сопоставить свой символ (0…9 и A…F, как показано в Табл. 1.3), то этот адрес можно будет записать в виде h’8СН0А’[14], что гораздо удобнее. Этот код называется шестнадцатеричным, поскольку для обозначения разрядов в нем используется 16 символов. Шестнадцатеричные числа (числа с основанием 16) — это вполне жизнеспособные самостоятельные числа, а не просто какое-то дополнительное представление двоичных чисел. Разряды шестнадцатеричного числа имеют веса соответственно 16⁰, 16¹, 16²…., 16ⁿ[15].

Двоично-десятичный код (Binary-Coded Decimal — BCD) является гибридом двоичного и десятичного представлений, широко используемым при работе с портами ввода/вывода цифровых устройств (см. Пример 11.5 на стр. 360). При таком представлении каждый десятичный разряд заменяется своим двоичным эквивалентом. Так, число 1998 записывается в виде (0001 1001 1001 1000)_BCD. Это представление очень сильно отличается от эквивалентного обычного двоичного кода, несмотря на то, что при его записи тоже используются только нули и единицы. Как и следовало ожидать, выполнение арифметических операций с числами, записанными таким образом, представляет собой не простую задачу. Поэтому, как правило, на входе системы BCD-числа преобразовываются в обыкновенные двоичные числа, а после обработки преобразовываются обратно (см. Программу 5.7 на стр. 159).

Двоичная арифметика[16] подчиняется тем же правилам, что и более привычная для вас арифметика по основанию 10. Более того, это утверждение справедливо для любой системы счисления. Простейшей арифметической операцией является операция сложения, представляющая сокращенную форму записи операции нахождения общего количества чего-либо по сравнению с более примитивным процессом счета или прибавления единицы. Так, запись 2 + 4 = 6 гораздо удобнее, чем 2 + 1 = 3, 3 + 1 = 4, 4 + 1 = 5, 5 + 1 = 6. Однако при этом необходимо помнить правила сложения. Для десятичных чисел существует 45 правил, если учесть, что порядок слагаемых не важен, — от 0 + 0 = 0 до 9 + 9 = 18. Двоичное сложение гораздо проще, поскольку подчиняется всего трем правилам:

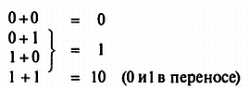
Сначала эти правила применяются к самым младшим значащим битам (Least Significant Bit — LSB); при возникновении переноса он передается в бит, расположенный левее. Процесс вычисления заканчивается старшими значащими битами (Most Significant Bit — MSB). Если из этой позиции происходит перенос, то именно он становится самым старшим битом суммы. Например:

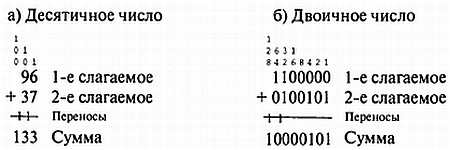
Подобно тому как при сложении осуществляется прямой счет, операция вычитания соответствует обратному счету, при котором от исходного значения отнимаются единицы. Так, операция 8–5 = 3 эквивалентна последовательности операций 8–1 = 7, 7–1 = 6, 6–1 = 5, 5–1 = 4, 4–1 = 3.

В соответствии с известной методикой вычитания десятичных чисел правила вычитания применяются и к двоичным числам, начиная с младших битов и заканчивая старшими. Для каждого бита, в котором из меньшего числа вычитается большее, из ближайшего старшего бита занимается единица. С учетом заема правила вычитания в двоичной системе имеют вид

0 — 0 = 0

¹0 — 1 = 1 Из старшего бита занимается 1

1 — 0 = 1

1 — 1 = 0

Например:

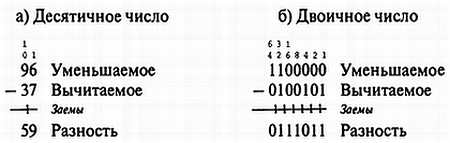
Несмотря на то что эти знакомые методы прекрасно работают, при реализации их в цифровых схемах возникает ряд проблем:

• Что делать, если вычитаемое меньше уменьшаемого?

• Как нам различать положительные и отрицательные числа?

• Можно ли выполнить вычитание с помощью блока суммирования?

Чтобы понять суть описанных проблем, взгляните на следующий пример:

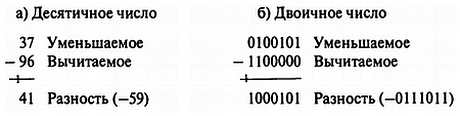
Обычно, если мы знаем, что уменьшаемое меньше вычитаемого, мы меняем операнды местами и добавляем знак минуса к результату, т. е. вычисляем выражение — (вычитаемое — уменьшаемое). Если мы не выполним такой перестановки, как показано в примере (а), приведенном выше, то результат окажется неверным. На самом деле число 41 является правильным в том смысле, что представляет собой разность между числом 59 (правильный результат) и 100. То есть число 41 представляет собой дополнительный код числа 59 в десятичной системе (10’s complement). Более того, сам факт заема из старшего разряда числа указывает на то, что результат операции отрицателен и представлен соответственно в дополнительном коде. Для преобразования числа, представленного в дополнительном коде, в «нормальный» вид достаточно просто проинвертировать каждый десятичный разряд и к полученному значению прибавить единицу. Инвертирование десятичного разряда заключается в вычитании его значения из 9. Таким образом, дополнительный код числа 3941 в десятичной системе равен —6059:

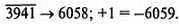
Как бы там ни было, единственной причиной, по которой мы не оставляем отрицательные числа в дополнительном коде, является непривычность для нас такого представления чисел.

Разумеется, использование дополнительного кода для представления отрицательных значений применимо и к двоичным числам. Причем, простота инвертирования (0 —> 1, 1 —> 0) делает этот метод очень привлекательным. Обратимся к приведенному выше примеру:

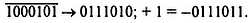
И опять же отрицательные числа следует оставлять в дополнительном коде (2’s complement)[17]. Обратите внимание, что операция преобразования в дополнительный код является обратимой, т. е.

дополнительный код <=> прямой код.

При работе с десятичными числами для обозначения положительных и отрицательных чисел используются знаки «+» и «—» соответственно. В системе же с двумя состояниями мы можем оперировать только единицами и нулями. Тем не менее, взглянув на последний пример, можно получить ключ к решению этой проблемы. Как уже было сказано, отрицательное значение получается в результате заема в старший разряд числа. Так что мы можем использовать этот разряд в качестве знакового бита (sign bit), причем 0 будет эквивалентен знаку «+», а 1 — знаку «—». Таким образом, число Ь’11000101’ будет соответствовать значению —59, а Ь’00111011’ — значению +59 (в примерах знаковый бит выделен полужирным шрифтом). Преимущество такого представления заключается в том, что при любых арифметических операциях с ним можно обращаться так же, как и с обычным битом. При этом результат операции будет иметь верный знак:

Из примера видно, что если отрицательное число представлено в дополнительном коде, то нам не нужно изобретать аппаратный «вычитатель», поскольку прибавление отрицательного числа эквивалентно вычитанию положительного. Другими словами, А — В = А + (—В). Более того, если числа будут записаны в дополнительном коде, результаты всех последующих арифметических операций также будут в дополнительном коде.

С арифметическими операциями над отрицательными числами, представленными в дополнительном коде, связаны две проблемы. Первая из этих проблем — переполнение (overflow). Она заключается в том, что при сложении двух положительных или двух отрицательных чисел может возникнуть переполнение в знаковом бите, например:

а) Сумма двух положительных чисел б) Сумма двух отрицательных чисел получается отрицательной получается положительной

В примере (а) результат сложения (+8) + (+11) равен —13. В данном случае произошло переполнение из четвертого значащего бита в знаковый (в действительности число 10011b = 19 является корректным результатом). В примере (б) показана та же ситуация при сложении двух отрицательных чисел. Переполнение может возникнуть только в том случае, если оба операнда имеют одинаковые знаковые биты. Поэтому для обнаружения переполнения следует отслеживать значение знакового бита результата, отличающееся от значения знаковых битов операндов. Логическая схема, реализующая обнаружение переполнения, показана на Рис. 1.5.

Вторая проблема касается выполнения арифметических операций над знаковыми операндами разной разрядности, например:

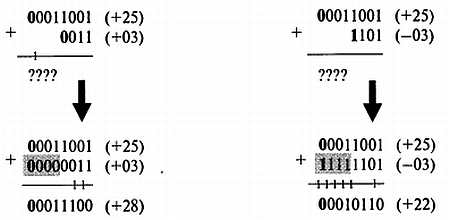
В обоих примерах показано сложение 8-битного числа с 16-битным. Если первый операнд положителен, его разрядность можно увеличить до 16 бит, заполнив свободные позиции нулями. Если же требуется расширить отрицательное число, то решение уже не так очевидно. В этом случае расширение числа производится путем заполнения пустых разрядов единицами. Общее правило звучит так: при расширении данных дополнительные разряды слева следует заполнять знаковым битом. Этот метод называется расширением знака (sign extension).

Умножение числа на n-ю степень двойки реализуется сдвигом исходного значения на n позиций влево. Таким образом, последовательность операций 00110 (6) << 01100 (12) << 11000 (24) эквивалентна умножению числа 6 на 22; оператор «<<» используется для обозначения сдвига влево. Это же правило применимо и к отрицательным числам:

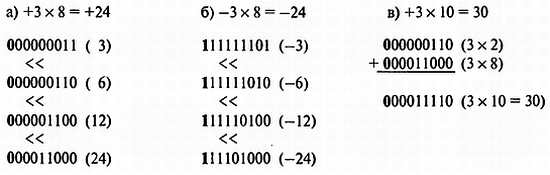
Смена значения знакового бита означает переполнение в старшем бите модуля числа. Некоторые компьютеры (микропроцессоры) поддерживают операцию арифметического сдвига влево, которая сигнализирует о такой ситуации в отличие от обычной операции логического сдвига влево, используемой для сдвига беззнаковых чисел.

Умножение на число, не являющееся степенью двойки, можно реализовать, комбинируя операции сдвига и суммирования. В частности, как показано в предыдущем примере (в), выражение 3x10 вычисляется следующим образом:

(3 х 8) + (3 х 2) = (3 х 10) или (3 << 3) + (3 << 1).

Аналогичным образом деление числа на n-ю степень двойки реализуется сдвигом значения на n позиций вправо, т. е. 1100 (12) >> 0110 (6) >> 0011 (3) >> 0001.1 (1.5). Этот же способ применим к знаковым числам:

Обратите внимание, что освободившиеся при сдвиге влево позиции заполняются не нулями, а содержимым знакового бита. Таким образом, при сдвиге положительных чисел слева вдвигаются нули, а при сдвиге отрицательных чисел — единицы. Данная операция известна как арифметический сдвиг вправо, в отличие от логического сдвига вправо, при котором всегда вдвигаются нули.

Деление на число, не являющееся степенью двойки, показано в примере (в). Эта операция осуществляется аналогично операции деления столбиком в десятичной системе. При ее выполнении по аналогии с умножением используется комбинирование операций сдвига и вычитания.

Арифметические действия — не единственные операции, которые можно осуществлять над двоичными числами. Английский математик Джордж Буль[18] (George Boole) в середине 19-го столетия создал раздел алгебры, касающийся символической обработки логических отношений. Этот раздел алгебры, называемый Булевой алгеброй, оперирует величинами, которые могут иметь только два состояния: истина или ложь. В 30-х годах стало понятно, что этот раздел математики может быть с успехом использован для анализа коммутационных схем и, соответственно, устройств двоичной логики. Мы ограничимся рассмотрением базовых логических операций этой алгебры переключательных схем.

Инверсия, или операция НЕ (NOT), обозначается символом надчеркивания. Таким образом, выражение f = А¯ означает, что переменная f является обратной величиной переменной А. То есть если А = 0, то f = 1, и, наоборот, если А = 1, то f = 0. На Рис. 1.1, а эта зависимость представлена в виде таблицы истинности (truth table). По определению двойная инверсия переводит переменную в первоначальное состояние: f⁼ = f[19].

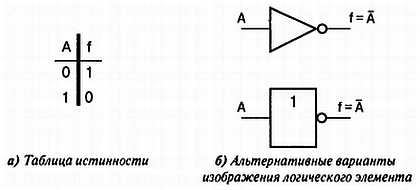
Рис. 1.1. Операция НЕ (NOT)

Как правило, реализации логических функций представляются с помощью абстрактных символов, а не подробных электрических схем. Общепринятое изображение элемента НЕ приведено на Рис. 1.1, б[20]. Кружок на изображении логических схем всегда означает инверсию и очень часто используется в сочетании с другими логическими элементами (см., например, Рис. 1.2, в).

Оператор И (AND) реализует функцию «все или ничего». Результат операции будет истинным только в том случае, если все n входов истинны. На Рис. 1.2 имеется две входные переменные, и выражение для выходного значения записывается как f = В∙А, где символ «» — булевый оператор И[21]. Количество входных переменных может быть любым, и в общем случае f = А(0)∙А(1)∙А(2)∙…∙А(n). Операцию И иногда называют операцией логического умножения, поскольку (по аналогии с обычным умножением) результат этой операции между любым битом и 0 всегда будет равен 0.

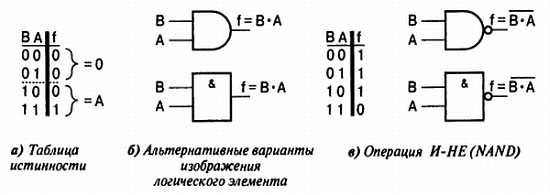
Рис. 1.2. Операция И (AND)

Если предположить, что вход В является управляющим входом, а вход А — входом данных, то, обратившись к таблице истинности, мы увидим, что при В = 1 на выходе будут присутствовать входные данные, а при В = 0 на выходе постоянно будет 0. Таким образом, эту схему можно рассматривать как управляемый вентиль. В общем случае термин вентиль применим к любой логической схеме, реализующей базовые логические операции.

В большинстве практических реализаций вентиля И используется инвертированный выход. Логическая функция такого элемента называется И-НЕ (NOT AND, или NAND), а ее изображение приведено на Рис. 1.2, в.

Действие оператора ИЛИ (OR) можно описать словом «что-нибудь». Результат этой операции будет истинным, если истинно хотя бы одно из входных значений (поэтому на символе изображено «>= 1»). Хотя элемент, показанный на Рис. 1.3, имеет только два входа, операция ИЛИ применима к любому числу входных переменных. Часто операцию ИЛИ называют логическим сложением, соответственно в качестве математического оператора используется знак «+»[22]:

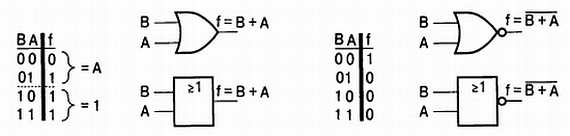
Рис. 1.3. Операция ИЛИ (OR)

Если предположить, что вход В является управляющим входом, а вход А — входом данных (или наоборот), то из Рис. 1.3, а видно, что данные проходят через вентиль при В = 0 и задерживаются (на выходе постоянно присутствует 1) при В = 1. Такое поведение отчасти похоже на инверсное действие функции И. В самом деле, функция ИЛИ может быть выражена через функцию И посредством двойственного соотношения 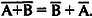. Из этого соотношения следует, что функцию ИЛИ-HE можно реализовать инвертированием сигналов, подаваемых на вход элемента И.

Мы познакомились с тремя основными логическими операторами: И, ИЛИ и НЕ. Однако существует еще одна операция, часто используемая в электронике, — операция Исключающее ИЛИ (exclusive OR — XOR). Функция XOR истинна, если истинен только один из входов (поэтому на символе изображено «=1», см. Рис. 1.4, б). В отличие от обычной операции ИЛИ, при 1 на обоих входах на выходе будет 0.

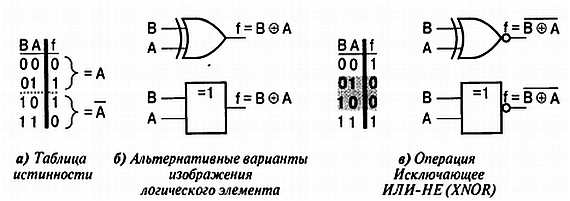
Рис. 1.4. Операция Исключающее ИЛИ (XOR)

Если предположить, что вход В — управляющий, а вход А — вход данных (или наоборот), тогда

• Если В = 0, то f = А — данные с входа передаются на выход.

• Если В = 1, то f = А¯ — выходной сигнал представляет собой инвертированный входной сигнал.

Таким образом, вентиль Исключающее ИЛИ может использоваться в качестве программируемого инвертора.

Другим полезным применением функции Исключающее ИЛИ можно назвать использование ее в качестве логического дифференциатора. Из таблицы истинности (Рис. 1.4, а) видно, что выход элемента Исключающее ИЛИ истинен только тогда, когда состояния обоих входов различны. Аналогично, из таблицы истинности оператора Исключающее ИЛИ-HE (XNOR), показанной на Рис. 1.4, в, видно, что выход такого элемента истинен при одинаковых сигналах на обоих входах. Таким образом, вентиль Исключающее ИЛИ-HE можно рассматривать в качестве 1-битного компаратора. Равенство двух «-битных значений можно проверить, объединив по И набор вентилей Исключающее ИЛИ-HE (см. Рис. 2.7 на стр. 37), каждый из которых реализует функцию , т. е.

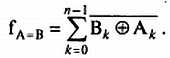
В качестве простого примера использования элементов Исключающее ИЛИ и Исключающее ИЛИ-HE рассмотрим задачу определения переполнения в знаковом бите (см. стр. 24). Эта ситуация возникает, если знаковые биты обоих операндов одинаковы 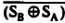, а знаковый бит С результата отличается от них, скажем 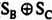. Схема такого детектора, показанная на Рис. 1.5, описывается логической функцией:

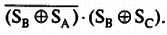
И наконец, функцию Исключающее ИЛИ можно использовать для определения четного количества истинных входов. При каскадном соединении n + 1 вентилей Исключающее ИЛИ выходной сигнал будет равен 1, если входное n-битное число содержит четное число единичных битов. Добавляя к слову данных дополнительный бит, так чтобы общее число битов было четным, можно реализовать простейшую защиту от ошибок. Приемное устройство будет контролировать четность принимаемых данных, и любое несоответствие будет означать их повреждение.

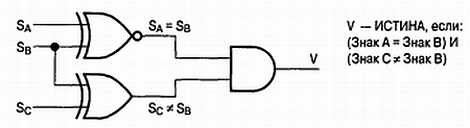
Рис. 1.5. Обнаружение переполнения в знаковом бите