4.2. Стойкость стегосистем к обнаружению факта передачи скрываемых сообщений

4.2. Стойкость стегосистем к обнаружению факта передачи скрываемых сообщений

Для анализа стойкости стеганографических систем к обнаружению факта передачи скрываемых сообщений рассмотрим теоретико-информационную модель стегосистемы с пассивным нарушителем, предложенную в работе [3].

Нарушитель Ева наблюдает сообщения, передаваемые отправителем Алисой получателю Бобу. Ева не знает, содержат ли эти сообщения безобидный контейнер С или стего S со скрываемой информацией. Будем полагать, что Алиса может находится в одном из двух режимов: она или активна (и тогда по наблюдаемому каналу передается стего S) или пассивна (передается пустой контейнер С). Когда Алиса активна, она преобразует контейнер С вложением в него скрываемого сообщения М, используя секретный ключ К. Допустимо построение стегосистемы, в которой Алиса может сама генерировать для скрытия сообщения М подходящий контейнер. Получив стего S, Боб должен быть способен извлечь из него сообщение М, используя ключ К. В терминах теории информации стегосистема должна удовлетворять соотношениям:

1. H(S/CMK) = 0. Формируемое отправителем стего S однозначно определяется значениями контейнера C, ключа К и сообщения М.

2. H(М) > 0. Неопределенность до момента передачи скрываемого сообщения М и для получателя и для нарушителя строго больше нуля, иначе по скрытому каналу не передается неизвестной для получателя информации и теряется смысл использования стегосистемы. Заметим, что это может не выполняться для систем ЦВЗ, целью которых является не передача неизвестной для получателя или нарушителя информации, а установление авторства передаваемого контейнера.

3. H(М/SK) = 0. Получатель Боб должен однозначно восстановить скрываемое сообщение М из принятого стего S, пользуясь ключом К.

Будем полагать, что вероятностные распределения множеств скрываемых сообщений, контейнеров, стего и ключей известны для всех участников информационного противоборства. Дополнительно получатель Боб знает, активна или нет отправитель Алиса. Ева, наблюдая передаваемые Алисой сообщения, должна установить передается по каналу связи скрываемая информация или нет. Для выявления факта использования стегосистемы Ева пытается определить, соответствуют ли передаваемый информационный поток распределению контейнеров или распределению стего. Если Ева способна установить, что в наблюдаемом канале передаются сообщения с распределением стегограмм, то факт скрытой передачи информации от Алисы к Бобу доказан, а используемая ими стегосистема является нестойкой. Сформулируем задачу доказательства стойкости стегосистемы как задачу различения гипотез.

В рассматриваемой модели стегосистемы известно вероятностное распределение пустых контейнеров, обозначаемое Р_С, и вероятностное распределение стегограмм, обозначаемое Р_S. Нарушитель в контролируемом канале связи может наблюдать множество возможных пустых контейнеров и стегограмм. Обозначим это множество возможных наблюдений Q. Нарушитель, наблюдая передаваемое сообщение q 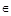Q, выдвигает две гипотезы Н_С и Н_S. Если справедлива гипотеза Н_С, то сообщение q порождено в соответствии с распределением Р_С, а если справедлива Н_S, то q соответствует распределению Р_S. Правило решения заключается в разбиении множества Q на две части так, чтобы назначить одну из двух гипотез каждому возможному сообщению q 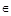Q. В этой задаче различения возможны два типа ошибок: ошибка первого типа, которая заключается в установлении гипотезы Н_S, когда верной является Н_С и ошибка второго типа, когда принято решение Н_С при верной гипотезе Н_S. Вероятность ошибки первого типа обозначается ?, вероятность ошибки второго типа — ?.

Метод нахождения оптимального решения задается теоремой Неймана-Пирсона. Правило решения зависит от порога Т. Переменные ? и ? зависят от Т. Теорема устанавливает, что для некоторого заданного порога Т и допустимой максимальной вероятности ?, вероятность ? может быть минимизирована назначением такой гипотезы Н_С для наблюдения q 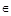Q, если и только если выполняются

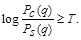(4.2)

Основным инструментом для различения гипотез является относительная энтропия (ОЭ) или различимость между двумя распределениями вероятностей P_С и P_S, определяемая в виде

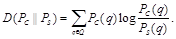(4.3)

Относительная энтропия между двумя распределениями всегда неотрицательна и равна 0, если и только если они неразличимы (совпадают). Хотя в математическом смысле ОЭ не является метрикой, так как она не обладает свойством симметричности и свойством треугольника, полезно ее использовать в качестве расстояния между двумя сравниваемыми распределениями. Двоичная относительная энтропия d(?,?) определяется как

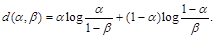
Используем относительную энтропию D(Р_с || Р_s) между распределениями Р_с и Р_s для оценки стойкости стегосистемы при пассивном противнике. В работе [3] дано следующее определение: стегосистема называется ?-стойкой против пассивного нарушителя, если

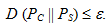
Если ? = 0, то стегосистема является совершенной.

Если распределения контейнера и стего одинаковы, то 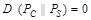, и такая стегосистема является совершенной. Это означает, что вероятность обнаружения факта передачи скрываемой информации не изменяется от того, наблюдает нарушитель информационный обмен от Алисы к Бобу или нет. Пассивный нарушитель, обладающий произвольно большими ресурсами и владеющий любыми методами стегоанализа, не способен обнаружить факт использования совершенной стегосистемы.

Рассмотрим условия обеспечения стойкости стегосистем. Известно соотношение между энтропией, относительной энтропией и размером алфавита |X| для произвольных случайных переменных S и С. Отметим, что контейнеры С и стего S принадлежат одному и тому же алфавиту Х. Если переменная S равновероятно и независимо распределена, то

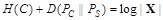. (4.4)

Если переменная С является равновероятно и независимо распределенной, то, как известно из теории информации [10], выполняется равенство 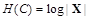и тогда 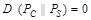. Следовательно, если в качестве контейнеров С использовать случайные последовательности и скрываемые сообщения будут описываться также случайными последовательностями, то сформированные стего S не будут иметь никаких статистических отличий от пустых контейнеров, и такая стегосистема будет совершенной. Если скрываемая информация представляет собой осмысленные сообщения, которые описываются последовательностями с неравномерными и зависимыми между собой символами, то к требуемому виду их легко привести путем шифрования любым стойким шифром.

Опишем пример формально совершенной стегосистемы, в которой контейнеры представляет собой последовательности независимых и равновероятных случайных бит и в качестве функции встраивания скрываемых сообщений используется известная криптографическая функция типа «однократная подстановка». Пусть контейнер С есть равновероятно распределенная случайная последовательность длиной n бит. Формирователь ключа генерирует случайную равновероятно распределенную последовательность ключа k длиной n бит и передает ее Алисе и Бобу. Если Алиса активна, то функция встраивания представляет собой побитное суммирование по модулю 2 для скрытия n-битового сообщения m, где стего формируется по правилу 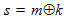. Получатель Боб извлекает скрытое сообщение вычислением 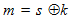. Сформированное стего S равновероятно распределено для последовательности n битов и поэтому 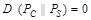. Таким образом, построение функции встраивания как однократной подстановки обеспечивает совершенность стегосистемы, если контейнер формируется равновероятным случайным источником.

Однако реальные передаваемые по каналам связи сообщения, используемые в стегосистемах как пустые контейнеры, далеки от модели безизбыточных и равновероятных источников. Поэтому передача зашифрованных описанным способом сообщений на фоне сообщений естественных источников сразу же демаскирует канал скрытой связи. Для стеганографии характерен случай неравновероятного распределения переменной С, описывающей выход естественного источника с некоторой существенной памятью. Сообщения таких источников обычно используются в качестве контейнеров (изображения, речь и т. п.) и их энтропия H(S) обычно значительно меньше величины 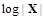. Для встраивания скрываемых сообщений из таких контейнеров удаляется часть избыточности и в сжатые таким образом контейнеры вкладываются скрываемые сообщения. В результате этого вероятностные характеристики формируемых стегограмм отличаются от характеристик пустых контейнеров, приближаясь к характеристикам случайного независимого источника. В предельном случае дискретные стегограммы описываются бернуллиевским распределением. В этом случае вся избыточность контейнера удалена и встроенное сообщение порождено равновероятным случайным источником.

Рассмотрим следующий пример. Пусть в качестве контейнеров используются сообщения типа «деловая проза» на русском языке, для которых известна оценка энтропии H(C) = 0,83 бит/буква [11]. Величина 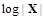для русского языка с алфавитом из 32 букв составляет log 32 = 5. Следовательно, в предельном случае относительная энтропия между обычными сообщениями с распределением Р_С и стегограммами с распределением Р_S равна

.

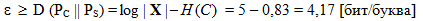Очевидно, что в этом случае безизбыточные стего, выглядящие как случайный набор букв русского языка, сразу же выделяются на фоне избыточных контейнеров, представляющих собой осмысленные сообщения. Таким образом, факт использования такой стегосистемы легко обнаруживается при визуальном просмотре передаваемых от Алисы к Бобу сообщений. При использовании такой стегосистемы также легко автоматизировать процесс поиска следов скрытого канала. Для этого достаточно подсчитывать приблизительные оценки энтропии передаваемых сообщений. Так как энтропия стего примерно в 5 раз больше энтропии обычных сообщений, то достаточно просто выявить факты наличия скрытой связи.

В работе [3] доказывается, что произвольные детерминированные преобразования не увеличивают ОЭ между двумя распределениями.

Лемма 1: Пусть Р_Qc и Р_Qs описывают вероятностные распределения контейнеров и стего, соответственно, над множеством наблюдений Q. Детерминированное отображение f преобразует множество наблюдений Q в множество наблюдений T вида

,

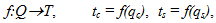где q_c, q_s 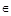Q, t_c, t_s 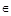T. Тогда справедливо выражение

.

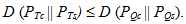Так как различение между гипотезами H_C и H_S есть частная форма преобразования, вероятности ошибок ? и ? удовлетворяют неравенству

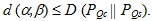. (4.5)

Это соотношение может использоваться в следующем виде: пусть ? есть верхняя граница 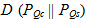и задана верхняя граница вероятности ?. Тогда выражение (4.5) дает нижнюю границу вероятности ?. Например, при ? = 0 значение ошибки .

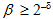Используя эту лемму, в работе [3] доказывается следующая теорема.

Теорема 2: Если стегосистема является ?-стойкой против пассивного нарушителя, то вероятность ? необнаружения факта скрытой связи и вероятность ? ошибочного установления факта скрытой связи удовлетворяют неравенству 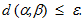. В частном случае, если ? = 0, то .

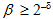Пусть Алисе разрешается передать Бобу цифровое изображение С. Используя модель чувствительности зрения, она может сформировать множество С эквивалентных изображений, которые визуально неразличимы от исходного С. Независимо от того, активна Алиса или нет, она передает выбранное изображение из множества С. Пусть Алиса и Боб заранее договорились, какой модификации изображения соответствует каждое из скрываемых сообщений. Формально это означает, что в стегосистеме каждому из изображений С_j, где j=1,2,…, |C|, по секретному ключу ставится в соответствие или одно из скрываемых сообщений М_j, где j=1,2,…, N, и N < |C|, или отсутствие скрываемого сообщения для |C|—N случаев. Если данное соответствие построено равновероятно и независимо для множества контейнеров и скрываемых сообщений, то при неразличимости распределений контейнеров и стего нарушитель Ева, наблюдая за информационным обменом между Алисой и Бобом, потенциально не способна получить больше той информации, которой обладала априори. Так как по определению Еве известны статистические характеристики всех множеств, входящих в стегосистему, то она априори знает, что вероятность активного состояния Алисы равна N/|C|, а вероятность отсутствия передачи скрываемой информации равна (|C|—N)/|C|. Активное и пассивное состояния Алисы составляют полную группу событий, следовательно,

.

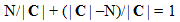Таким образом, если Алиса собирается передавать N скрываемых сообщений под прикрытием |C| контейнеров, то вероятность того, что Ева угадает, что произвольный контейнер содержит вложенную информацию не может быть меньше величины N/|C|. Если стегосистема совершенна, то вероятность угадывания нарушителем факта передачи скрываемого сообщения строго равна этой величине.

Из этого следует, что вероятность пассивного состояния Алисы должна быть во много раз больше вероятности ее активного состояния, и что используемых контейнеров с учетом их модификаций должно быть во много раз больше скрываемых сообщений. Перефразируя известную поговорку, можно сказать, что иголку более надежно можно спрятать от чужих глаз в большом стоге сена, чем в маленьком.

Рассмотрим влияние некоторой дополнительной информации на распределения контейнеров и стего и, соответственно, на стойкость стегосистемы. Пусть некоторые внешние события влияют на распределение контейнеров, например, выпуски новостей или погоды в известной «задаче заключенных». Эта дополнительная информация обозначается Y и известна всем участникам. Соответственно изменим нашу модель и определение стойкости. Определим средние вероятности вида 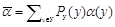для ошибки 1 рода и 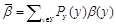для ошибки 2 рода, где ?(y) и ?(y) означают, соответственно, величину вероятностей ошибок 1 и 2 рода для Y = y.

Условная относительная энтропия (УОЭ) между Р_С и P_S, принадлежащих одному алфавиту Х, зависимая от переменной Y, определяется в виде

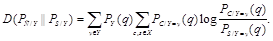(4.6)

Из неравенства Иенсена [10] и из выражения (4.5) следует, что

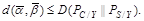(4.7)

Стегосистема с дополнительной информацией Y, контейнерами С и стего S называется ?-стойкой против пассивного противника, если условная относительная энтропия 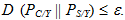. В качестве примера использования в стегосистеме внешней информацией укажем «классическую» задачу Г.Симмонса, в которой заключенные скрытно обмениваются информацией о побеге. Вероятность передачи сообщения о побеге в темную ночь выше по сравнению со светлой ночью. Это общеизвестный факт не только для лиц, совершающих побеги, но и для их тюремщиков, ужесточающих контроль за возможными каналами скрытой передачи информации. Поэтому использование общеизвестной дополнительной информации в стегосистеме облегчает задачу нарушителя. Можно сказать, что ?-стойкая стегосистема с дополнительной информацией Y обеспечивает более высокую скрытность связи по сравнению с аналогичной ?-стойкой стегосистемой без этой информации.

Данный текст является ознакомительным фрагментом.