4.5. Теоретико-сложностный подход к оценке стойкости стеганографических систем

4.5. Теоретико-сложностный подход к оценке стойкости стеганографических систем

Рассмотренные в работах [2], [3] информационно-теоретические модели стойкости стеганографических систем имеют существенные недостатки. Впервые на это было обращено внимание в статье [19]. Как отмечено в этой работе, успешно применяемые для анализа криптосистем информационно- теоретические методы плохо подходят для анализа стегосистем. Причина этого в том, что процедура обнаружения скрытого сообщения не может быть смоделирована как непрерывный процесс. В самом деле, нарушитель может получить лишь два результата анализа подозрительного канала связи: либо он обнаружит факт присутствия стегосистемы, либо нет. Таким образом, мы имеем дело с прерывистым процессом, к которому неприменимы методы теории информации. В криптографии не так, там нарушитель может получать частичное знание об открытом сообщении (или ключе), и тем не менее система будет практически стойкой. Стегосистема же обязана быть совершенно стойкой по Шеннону. На рис. 4.11 на качественном уровне показана разность между криптосистемами и стегосистемами.

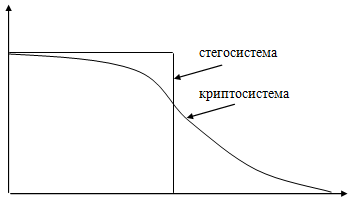
Рис. 4.11. Сравнение криптосистем и стегосистем. По оси ординат отложена степень секретности систем, по оси абсцисс — вычислительные ресурсы нарушителя

Осознание факта малопригодности информационно-теоретических моделей для анализа стегосистем повлекло за собой появление теоретико-сложностных подходов к оценке их стойкости [20]. В этой работе по-новому рассмотрено понятие стойкости стегосистем и построена конструктивная модель стойкой стегосистемы в виде вероятностной полиномиальной по времени игры между нарушителем и скрывающим информацию. К основным недостаткам информационно-теоретических моделей стегосистем можно отнести следующие.

1) Также как и в криптографии, на практике невозможно реализовать совершенно стойкую стегосистему. Можно показать, что реализация такой стегосистемы сводится к одноразовому блокноту (так называемому шифру Вернама). Таким образом, информационно-теоретические модели стегосистем неконструктивны.

2) Распределение вероятностей контейнеров на практике неизвестно, или известно с точностью до некоторой весьма и весьма приблизительной модели.

3) Используемые контейнеры отнюдь не являются реализацией случайного процесса, а, чаще всего, оцифрованными образами реальных физических объектов.

4) Вполне реалистично было бы предположить, что нарушитель имеет доступ лишь к ограниченным вычислительным ресурсам. Как и в криптографии достаточно потребовать, чтобы стегосистема выдерживала бы все полиномиальные тесты по ее обнаружению. Этот момент также не учитывают информационно-теоретические модели.

Рассмотрим модель стегосистемы, предложенную в работе [20]. Предположим, что имеется множество возможных контейнеров 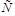, элементы которого 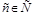порождаются некоторым полиномиальным алгоритмом. Встраиваемое сообщение 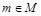, выбирается из множества возможных сообщений 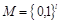. Стегосистема определяется тройкой 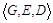полиномиальных алгоритмов.

Алгоритм G есть процесс генерации ключа, который в ответ на входную строку из единиц порождает псевдослучайный стегоключ 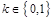. В соответствие с принципом Керхгофа стойкость зависит от ключа, а его длина является параметром секретности стегосистемы. Алгоритм E выполняет внедрение информации, формируя на основе 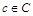, 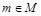и k, стего 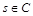. Алгоритм D извлекает из s с использованием ключа k сообщение m. В случае, если контейнер s действительно содержал встроенное сообщение, то 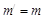. Для определения наличия стегосистемы нарушитель должен решить следующую задачу:

на основе контейнера 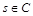определить, существует ли ключ 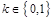, порождаемый G и сообщение 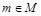такие, что .

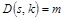Интересно отметить, что если на структуру скрытого сообщения не накладывается никаких ограничений, то для многих стегосистем эта задача неразрешима. В самом деле, любая комбинация бит может быть вложением, и даже если нарушитель каким-то образом и заподозрит наличие скрытой связи, все равно ему невозможно будет доказать это третьей стороне. Поэтому, в работе [20] на структуру скрытого сообщения накладывается ограничение: оно должно иметь какой-то семантический смысл.

Далее, считается, что у нарушителя имеется стегосистема в виде «черного ящика», то есть он имеет возможность порождать стего из выбираемых им контейнеров и скрытых сообщений, не зная при этом ключа. Для этой цели у него имеется два оракула: один для генерации пустых контейнеров (стеганографический оракул), другой — для получения из них стего, то есть имитации алгоритма внедрения (оракул оценки). Так как оба оракула вероятностные, то в случае выбора первым оракулом несколько раз подряд одного и того же контейнера, стего будут получаться различными. Это помогает нарушителю выяснять структуру алгоритма внедрения, выбрав в качестве контейнера, например, однотоновое изображение.

Атака (игра) заключается в следующем. Нарушитель имеет неоднократную возможность генерировать контейнеры и соответствующие им стего, пытаясь выяснить структуру стегоалгоритма. При этом имеется то ограничение, что вся процедура должна быть полиномиальной по длине ключа и размеру контейнера. После того, как он закончил работу, ему предъявляются два случайно выбранных контейнера: один пустой, другой — заполненный. Стегосистема называется условно стойкой, если у нарушителя нет возможности правильного определения стего с вероятностью, незначительно отличающейся от 1/2. В работе [20] дано определение понятия «незначительно отличающейся» и приведено математическое описание вербально изложенной выше модели. Условно стойкая стегосистема сохраняет это свойство для всех возможных ключей и всех возможных контейнеров.

Ясно, что понятие условно стойкой стегосистемы более слабое, чем понятие стегосистемы, стойкой с информационо-теоретической точки зрения и включает ее как частный случай. Безусловно стойкая стегосистема в приведенной выше модели получается в случае, если снять ограничение полиномиальности во времени игры.

Каким образом построить условно стойкую стегосистему? Одна из возможностей, широко используемая и в криптографии, заключается во взятии за основу какой-нибудь трудной в вычислительном смысле математической задачи, например, обращение односторонней функции (разложение на множители, дискретное логарифмирование и т. д.). Тогда останется показать связь между невозможностью решения этой задачи и невозможностью вскрытия стегосистемы — и условно стойкая стегосистема построена. Из криптографии известно, что, к сожалению, вопрос построения доказуемо односторонней функции нерешен. В работе [20] показано, как можно построить стегосистему на основе известного криптоалгоритма RSA.

Данный текст является ознакомительным фрагментом.