53. Критическая скорость

We use cookies. Read the Privacy and Cookie Policy

53. Критическая скорость

Анализ формулы для скорости истечения показывает, что при уменьшении значения p2/p1 увеличивается скорость потока. Это возможно, например, если pi = const, а давление p2 уменьшается.

Из опытов известно, что уменьшение давления на выходе суживающегося сопла (или сопла постоянного сечения) p2 может осуществляться лишь до некоторого предельного значения, так называемого критического давления (pкритич). При этом критическим отношением давлений называется величина b= pкритич/p1, отсюда Pк = bp1

В результате уменьшения давления p0 (внешней среды) при p1= const возможны два случая:

1) po ? Pк, т. е. пока давление po уменьшается до критического значения, соблюдается равенство p2= po где p2 – давление вещества на выходе суживающегося сопла, po – давление внешней среды;

2) po < Pк, т. е. дальнейшее падение давления po среды ниже критического значения определяется равенством p2 = pk,причем давление p2 вытекающего вещества является постоянным (p2= const).

Таким образом, явление, при котором в устье насадки давление постоянно и не понижается, называется запиранием сопла. Поэтому такое давление на выходе сопла, которое невозможно понизить путем уменьшения давления внешней среды, в которую осуществляется истечение рабочего тела, называют критическим(P2к).

Независимо от падения давления внешней среды po в устье суживающегося сопла при bk устанавливается давление P2к=const, которому соответствует Gmax = const (массовый расход), wk = const (скорость истечения), Tk = const (температура), и v2k = const (удельный объем), т. е. постоянство всех параметров на выходе сопла (так называемые выходные параметры).

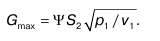
В полученных формулах a, Y – коэффициенты, определяемые только величиной k(показателем адиабаты), их значения находят из специальных таблиц.

По определению критической скоростью называется наибольшая скорость вещества при его истечении из сопла, не превышающая скорость звука, т. е. wk =a, где а – так называемая местная скорость звука.

Полученная формула называется уравнением Лапласа.

Данный текст является ознакомительным фрагментом.