6.4. Редактирование сюжетов иллюстраций

6.4. Редактирование сюжетов иллюстраций

При работе над иллюстрациями важно оценить точность пере–дачи содержания сюжета (это относится прежде всего к рисункам творческого характера). Отредактировать технический рисунок – значит выявить и подчеркнуть то, что особенно важно для данного произведения (издания). Для этого используют кадрировку, позво–ляющую выделить малозаметную деталь на общем изображении, утолщение линий, штриховку. Фотографии должны быть осво–бождены от случайных деталей, не имеющих отношения к теме и отвлекающих внимание читателя. Редактирование сюжетов чер–тежей, схем, графиков требует знания основ чертежной техники. Приведем примеры редактирования графиков.

График помогает понять главное, существенное в эксперимен–тальных или статистических данных, на основе которых он по–строен. Графическое изображение предполагает его зрительный анализ, соотношение различных показателей. Читатель, полагаю–щийся лишь на зрительное восприятие, может прийти к неверным выводам. Умение обнаружить некоторые ошибки в иллюстрациях – залог успеха будущего издания.

Иногда в графиках выбирают неверный масштаб, что является причиной ложных представлений о сути явления. Чтобы проил–люстрировать это, приведем графики, выполненные в разных масштабах (примеры 3, 4).

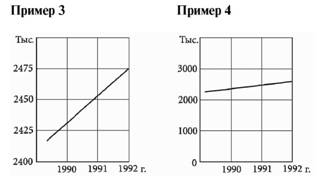
Эти графики выражают одну и ту же зависимость, но воспри–нимаются неодинаково. График на рисунке (пример 3) с круто взметнувшейся вверх параметрической линией создает впечатление интенсивно прогрессирующего процесса, тогда как на самом деле (пример 4) этот прогресс более чем скромен. Конечно, если бы на оси ординат графика была помещена полная шкала, начинающаяся с нуля, ошибочного впечатления у читателя не возникло бы.

Как правило, графики приводят с сеткой. Ее не приводят на графиках, поясняющих только характер изменения функции, в этом случае на осях числовые значения величин не указывают (пример 5). Без сетки допускается приводить графики и с отло–женными числовыми значениями величин, но только в том слу–чае, если наличие сетки ухудшит наглядность рисунка, затруднит его восприятие (пример 6).

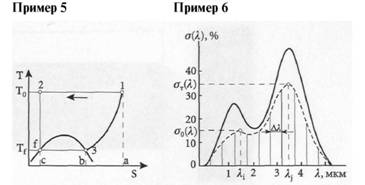
На графиках указывают наименование и единицу величины, числовые значения которой помещены у делений шкалы на осях.

Буквенное обозначение или развернутое наименование величи–ны, написанное вдоль оси с прописной буквы отдельной строкой, отделяют от единицы величины запятой (примеры 7, 8).

При наличии нескольких шкал по вертикальной (или горизон–тальной) оси их проводят рядом с основной осью, т.е. слева от вер–тикальной оси или под горизонтальной осью. При этом числовые значения пишут слева от вертикальных осей и ниже горизонталь–ных осей. Буквенное обозначение наименования и единицу вели–чины отделяют запятой и указывают над числовыми значениями для вертикальных осей и рядом с числовыми значениями для го–ризонтальных осей (примеры 8, 9).

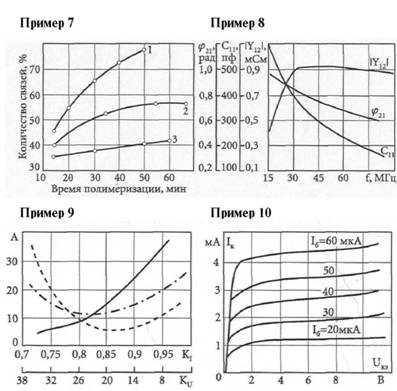
Для справочников или других изданий, содержащих большое количество иллюстраций в виде графиков, допускается буквенное обозначение наименования величины писать на поле графика вверху, справа от вертикальной оси, и в конце над горизонтальной осью, единицу величины – над числовыми значениями по верти–кальной оси и за числовыми значениями по горизонтальной оси (пример 10).

Если шкалы осей координат начинаются с одной и той же циф–ры (или ноля), то эта цифра (или ноль) у их пересечения ставится один раз (примеры 6, 10), если с разных числовых значений, ста–вятся оба значения (примеры 7, 8, 9).

Характерные точки графиков (результаты опытов, точки пере–гиба и т.д.) изображают кружками. Их оставляют на графике в ми–нимальном количестве или исключают, если в тексте не приведены подробности опыта (примеры 6, 7).

Кривые графиков различаются тем, что либо вычерчиваются разными линиями (непрерывной, штриховой, тонкой, жирной и т.п.), либо обозначаются цифрами – порядковыми номерами (примеры 7, 9). Во всех случаях значение величины на каждой кривой поясняется в подписи к графику. Если кривые различают–ся значением какого-либо третьего фактора (два отложены на осях), пишут буквенное обозначение наименования величины и числовое значение этого фактора с единицей величины для пер–вой и последней кривых. Для промежуточных кривых указывают только числовое значение фактора (пример 10).

Иногда кривые, изображенные на нескольких графиках, можно совместить. Авторы приводят их на отдельных рисунках из-за того, что получают данные не сразу, а в течение какого-то времени, обобщить же полученные результаты, представить их в более ком–пактном виде им иногда не приходит в голову, тем более что они не ставят перед собой задачу сэкономить бумагу, об этом должен ду–мать редактор. Например, графики (примеры 11 и 12) можно объе–динить в один. Сетка не нужна, так как графики не расчетные, а иллюстративные. Словесные надписи на осях можно заменить об–щепринятыми условными обозначениями, а текст на иллюстраци–ях перенести в подрисуночную подпись. Вариант исправления приведен на рисунке (пример 13).

Пример 11

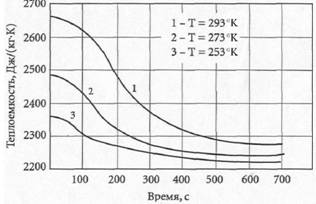
Зависимость теплоемкости продукта от времени при разной температуре окружающей среды

Пример 12

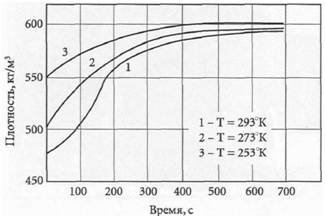
Зависимость плотности продукта от времени при разной температуре окружающей среды

График, как правило, показывает, как одна величина (функция) меняется в зависимости от изменений другой величины (аргумента). На оси абсцисс (обычно горизонтальная) откладывают значения аргумента, на оси ординат – значения функции.

Пример 13

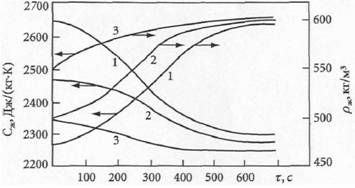
Изменение во времени теплоемкости Сж и плотности рж жидкого продукта при разной температуре окружающей среды Т: 1 – Т = 293°K; 2 – 273°K; 3 – 253°K

Приведем иллюстрацию из журнала «Жилищно-коммунальное хозяйство» (2003. № 3) и комментирующий ее текст (пример 14).

Пример 14

Поступление денежных средств на расчетный счет ЕРКЦ в тече–ние месяца происходит неравномерно. В Тутаевском муниципальном округе основной пик платежей приходится на 18—25-е число. <…> Примерный график поступления средств представлен на рисунке.

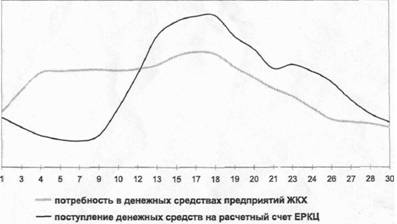
График потребности в денежных средствах практически не совпа–дает с графиком их фактического поступления. Денежные средства нужны для выплаты заработной платы (в среднем 15-е число), уплаты ЕСН (15-е число), уплаты НДС (20-е число).

Из рисунка видно, что денежные средства поступают неравно–мерно. Но из-за того, что на оси ординат нет обозначений (денеж–ные средства в абсолютном или относительном выражении), труд–но понять, почему нет средств на выплату зарплаты и уплаты ЕСН 15-го числа. Судя по начертанию кривых, именно на 14—18-е числа приходится пик денежных поступлений. Ось абсцисс показывает числа месяца с 1-го по 30-е, однако на оси их лишь 21, пропуски чисел 2, 6, 8 и других никак не отразились на величине делений оси – они все одинаковые.