27. Логарифмическая история Вселенной

Попытка представить огромное скопление галактик, спрессованное в сферу диаметром 10 мкм, перекручивает мозг в бараний рог. Если без предисловий рассказать про данный факт человеку, далекому от космологии, он скорее всего скажет, что это ерунда, что такого быть не может — здравый смысл протестует! При этом никаких рациональных аргументов против человек сформулировать не сможет. Чтобы урезонить здравый смысл, надо приучить его к логарифмической шкале явлений. Кстати, шкала, доступная непосредственному восприятию человека, не как уж коротка. Безо всяких устройств наш глаз способен окинуть сотню километров ландшафта, оценив расстояние, и разглядеть детали в одну десятую миллиметра. Это девять десятичных порядков. Во времени человек воспринимает даже больший диапазон — от десятой доли секунды почти до века — десять порядков. История Вселенной простирается от планковского времени (10^-43 с) до нынешнего (410^-7 с) — 60,5 порядка. Нынешний размер Вселенной неизвестен — он может быть как 10³¹, так и 10¹⁰⁰ см. Но можно взять за максимальный масштаб размер современного горизонта 5 10²⁸ см. Тогда диапазон расстояний, начиная от планковского масштаба и кончая горизонтом, — 61 порядок. Теперь можно изобразить историю Вселенной в дважды логарифмической шкале. Для начала проследим судьбу квантовых флуктуаций — как они росли и развивались после инфляции.

Здесь важно выбрать удобную систему отсчета для времени. Мы не знаем, сколько продолжалась инфляция, — как показано в следующей части, ее продолжительность могла быть любой. По сути, у нас есть только одна точка, за которую мы можем зацепиться — окончание инфляции и переход к фридмановской стадии. Треки на рис. 27.1 начинаются от времени 10^-37 с, характеризующего темп инфляции, — это условность, на самом деле переход от инфляции к фридмановскому расширению происходил не мгновенно. Саму инфляцию откладываем в отрицательную область, нуль будет ее окончанием. Ее удобней изобразить в линейной шкале на отдельном рисунке (рис. 27.2).

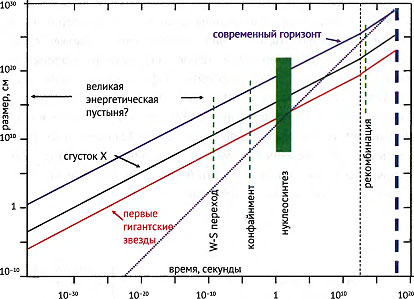
_{Рис. 27.1. История Вселенной после инфляции в дважды логарифмическом масштабе. Линиями показано, как менялся со временем размер области пространства, ставшего видимой частью Вселенной (горизонт), большой галактикой (сгусток X) и первыми гигантскими звездами. Вертикальные пунктиры показывают фазовые переходы материи во Вселенной. Наклонный пунктир показывает размер горизонта}

Когда инфляция заканчивается, треки выходят на степенную зависимость а ~ t^1/2 (степенной закон в дважды логарифмической шкале выглядит как прямая линия с наклоном, равным показателю степени). Такой закон расширения возникает из решения уравнения Фридмана для вселенной, в которой доминируют ультрарелятивистские или безмассовые частицы. Такая ситуация продолжается до t ~ 3·10¹² с (80 тыс. лет, незадолго до эпохи рекомбинации), после чего в балансе энергии Вселенной начинают доминировать холодные частицы (темная материя и барионы). При этом меняется уравнение состояния Вселенной — давление падает почти до нуля, и закон расширения меняется на а ~ t^2/3 (см. главу 13).

В самом конце добавляется новое экспоненциальное расширение, связанное с темной энергией, но пока оно слишком мало, чтобы его можно было увидеть в масштабе рисунка.

Прямая линия, пересекающая весь рисунок, — размер горизонта. При инфляции практически все флуктуации плотности, кроме самых последних, очень быстро растягиваются за пределы горизонта и таким образом «замораживаются». Возмущение не может эволюционировать, когда оно распределено по множеству причинно не связанных областей. После инфляции расширение становится медленней роста горизонта, и флуктуации вновь входят под горизонт — сначала те, что поменьше, потом большего размера. Скорость роста масштабов увеличивается на отметке времени 80 тыс. лет и приводит к формированию наблюдаемой структуры уже в возрасте вселенной во многие миллионы и миллиарды лет — в довольно узкой полосе в масштабе рисунка. Об этом более подробно рассказано в следующей главе.

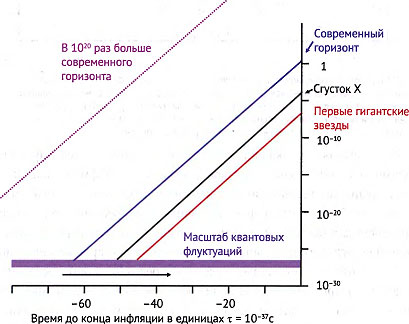
_{Рис. 27.2. Рост масштабов неоднородностей во время инфляции. Сиреневая полоса обозначает пространственный масштаб, на котором всё время до ? = 0 рождаются квантовые флуктуации. Линии показывают, как растут неоднородности, соответствующие будущим знакомым нам объектам. Поскольку продолжительность инфляции не имеет четкого ограничения, она могла продолжаться и тысячу единиц времени — тогда треки роста первых флуктуаций придут к ? = 0 на метр выше начала координат, достигнув значения порядка 10⁵⁰⁰ см — вполне возможно что Вселенная имеет такой или еще больший размер. Линии для простоты изображены прямыми — на самом деле при подходе к ? = 0 темп инфляции снижается и линии плавно загибаются.}

Наша эпоха, когда существуют планетные системы и возможна жизнь, в данном масштабе не больше ширины штрихов линии, обозначающей современную Вселенную на рис. 27.1 (справа). А между стадией инфляции и электрослабым фазовым переходом лежит самая долгая в логарифмическом плане эпоха, про которую мы мало что можем сказать. Есть подозрение, что в эту эпоху не происходило ничего интересного: по своей температуре эпоха соответствует так называемой Великой энергетической пустыне — области от сотен гигаэлектронвольт до 10¹⁶ ГэВ. Вероятно, где-то там сформировалась барионная асимметрия, возможно, жили разнообразные супер-симметричные партнеры нынешних частиц — фотино, скварки… Конечно, никто не даст голову на отсечение, что и посредине пустыни не происходило что-то интересное, просто это никак не просматривается из физики частиц в ее современном состоянии.

Могли ли на этом логарифмически длиннейшем отрезке истории случиться «искусства, знанья, войны, троны и память сорока веков»? Для этого прежде всего нужны частицы с массой, на много порядков превосходящей температуру Вселенной. Сейчас температура 3·10^-4 эВ — масса электрона на 9 порядков больше. В принципе, такие частицы могли остаться от эпохи окончания инфляции — с массой чуть меньшей, чем масштаб великого объединения, скажем, 10^-5 ГэВ. Допустим, есть какой-то закон сохранения, заставляющий эти частицы жить долго, например 1 не — до конца эпохи энергетической пустыни. Вполне возможно, что они могли бы образовывать что-то вроде атомов и молекул.

Однако, первая проблема заключается в том, что этих частиц оказалось бы маловато внутри горизонта Вселенной того времени. К концу эпохи энергетической пустыни таких частиц внутри горизонта оказалось бы где-то 10⁵⁰ — на 30 порядков меньше, чем барионов внутри нынешнего горизонта. Это число примерно того же порядка, что число барионов в Земле. Явно мало, учитывая, что пространство внутри горизонта быстро расширяется.

Следующая проблема заключается в том, что эти частицы не успели бы сконденсироваться в космические тела. И, наконец, достаточно ли 1 не для эволюции структур в их естественном масштабе времени? Вопрос о том, что такое естественный масштаб времени, не так прост, но, вероятно, для очень грубой оценки можно использовать единицы атомного времени, определяемого с помощью принципа неопределенности как t ~ ћ/E, где Е — энергия связи электрона в атоме. Для внешних оболочек в атоме примем Е = 10 эВ, тогда характерное атомное время будет 10¹⁶ с. За последние 3 млрд лет (10^-7 с) прошло 10³³ атомных времен. Этого хватило на всё.

Энергия связи электрона в атоме по меньшей мере на пять порядков меньше массы электрона. Наши гипотетические частицы эпохи конца Великой энергетической пустыни имеют массу не более 10¹⁵ ГэВ, и если следовать аналогии, то энергия связи в гипотетических атомах должна быть не больше 10¹⁰ ГэВ. Соответствующее атомное время — 10^-34 с. В таком случае за интересующую нас эпоху в 1 не прошло 10²⁵ атомных времен, что соответствовало бы 30 годам в пересчете на наши атомы. Явно мало.

Таким образом, за длинную, богатую метаморфозами логарифмическую историю Вселенной только наш короткий интервал в пол-порядка богат на сложные эволюционирующие структуры. А гораздо больший интервал в 14 порядков и впрямь остается пустынным.