13. Отталкивающая гравитация

В этой главе автор допускает некоторое занудство, приводя подробную серию выкладок, чтобы дотошный читатель мог проследить, как и откуда берутся парадоксальные явления, связанные с появлением Вселенной на свет. Здесь уже нет уравнений в частных производных, только обыкновенные простейшие дифференциальные уравнения, метод решения которых изложен на врезке.

Выше мы допустили, что пространство может быть заполнено неким скалярным полем, которое мы напрямую не ощущаем. Сейчас мы знаем по крайней мере один пример фундаментального скалярного поля — поле Хиггса. Квант этого поля (бозон Хиггса) недавно открыт на Большом адронном коллайдере. Еще одним примером скалярного поля может оказаться темная энергия, доминирующая в плотности энергии современной Вселенной, хотя в этом случае возможны разные интерпретации.

Абстрагируясь от конкретных примеров, предположим, что Вселенная заполнена однородным и постоянным во времени скалярным полем. Допустим, это поле имеет ненулевую плотность энергии, которую обозначим, как ?. Как это поле будет влиять на Вселенную?

Чтобы правильно вставить скалярное поле в уравнение Фридмана, осталось выяснить его уравнение состояния: как давление скалярного поля зависит от его энергии. Представим себе чудесный ящик (чудесный, поскольку в реальном мире такое воспроизвести невозможно), заполненный скалярным полем, вне которого поле равно нулю. Пусть у ящика есть выдвижная стенка с ручкой, которую можно вытягивать, увеличивая объем ящика. Потянем за стенку, отодвинув ее наружу на расстояние l. Объем ящика с полем увеличился на sl, где s — площадь стенки ящика. Значит, энергия поля в ящике увеличилась на ?sl. Она увеличилась за счет того, что мы совершили работу Fl, где F — сила, с которой мы тянули, — она равна -ps (минус появляется из-за того, что сила направлена против давления). Итак, приравнивая работу приращению энергии, имеем ?sl = -psl, значит, уравнение состояния (т.е. связь между плотностью энергии и давлением) для однородного и постоянного во времени скалярного поля: р = -?.

Это особое уравнение состояния: единственное с ненулевой плотностью энергии, которое лоренц-инвариантно, т.е. не выдаст наблюдателю, с какой скоростью он движется. Наблюдатель в любой системе отсчета будет «видеть» то же самое: плотность энергии ?, давление р = -?. Сравним с пространством, заполненным пылью: в системе отсчета, где пыль покоится, наблюдатель видит плотность энергии рс², давление 0. Для наблюдателя, движущегося с лоренц-фактором ? относительно пыли, плотность энергии равна ?²рс², кроме того, с его точки зрения в тензоре энергии-импульса появляются недиагональные элементы (компоненты импульса частиц пыли).

Благодаря лоренц-инвариантности такое уравнение состояния называют «вакуумным», подразумевая под вакуумом среду, которая не содержит частиц или переменных полей, не имеет температуры, лоренц-инвариантна, но не обязательно имеет нулевую плотность энергии.

Отрицательное давление само по себе не должно сильно удивлять. Из бытовых явлений самую близкую по смыслу демонстрацию дает поверхностное натяжение. Закрыв глаза на то, что это двумерный случай, имеем аналогию: мыльный пузырь. Поверхностное натяжение на пузыре не зависит от размеров последнего, при надувании пузыря любой элемент его поверхности не меняется, только поверхность становится более плоской. Вспомним теперь демонстрацию расширяющейся Вселенной в виде надуваемого шарика и заменим резиновый шарик на мыльный пузырь — на поверхности ничего нарисовать нельзя, зато состояние элемента «пространства» при надувании не меняется. Натяжение остается прежним.

Вернемся к вселенной, заполненной скалярным полем. Мыльный пузырь за счет поверхностного натяжения стремится сжаться — если из пузыря внезапно исчезнет воздух — он сожмется. А вселенная?

Оказывается, отрицательное давление (натяжение) заставляет вселенную расширяться с ускорением.

Чтобы показать это, снова обратимся к уравнению Фридмана. Выше мы выписали его для двух вариантов уравнения состояния — пылевидного (р = 0) и ультрарелятивистского (р = 1/3 ?). Сделаем это для общего случая пропорциональной зависимости р = ??. Как меняется плотность энергии с изменением масштабного фактора? Во-первых, она меняется с изменением объема как

d? = -dV?/V · ? = -3da?/a

Во-вторых, плотность энергии меняется из-за того, что давление совершает работу:

d? = -pdV/V = -3pda/a,

в сумме:

d?/da = -3(p + ?)/a = -3? · (1 + ?)/a

Решение этого уравнения:

? = ?₀ a^-3(1+?)

где ?₀ — константа размерности плотности энергии, конкретное значение которой зависит от выбора времени отсчета; положим а = 1.

Подставим его в уравнение Фридмана:

?/a = ?(8?/3G?₀)· a^-3/2(1+?)

или

da/dt = H₀·a^1-3/2(1+?)

Константа Н₀ = 8?/3G?₀ имеет размерность, обратную времени, — это не что иное, как постоянная Хаббла в момент, когда мы зафиксировали а = 1. Чтобы не мучиться с размерным временем в разных степенях, обезразмерим его, положив далее t = t_r Н₀, где t_r — время, выражаемое, например, в секундах, а постоянная времени 1/Н₀ зависит от того, на каком промежутке истории Вселенной мы работаем, — это может быть 10^-37 с, если речь идет о самой ранней Вселенной, или 10 млрд лет для современной.

Решение уравнение Фридмана с таким безразмерным временем (см. врезку):

a = t^{2/3 1/(1+?)}

Если ? = -1, т.е. р = -?, как в вакууме, то показатель степенной зависимости от времени становится бесконечным — в этом случае масштабный фактор растет экспоненциально (см. ниже). Если ? = -1/3, то рост идет по линейному закону с постоянной скоростью: а = t. Если ? > -1/3, то показатель степени меньше единицы и расширение идет с замедлением. А если -1 < ? < -1/3, то расширение пространства ускоряется со временем.

Ускоренное расширение при р < -1/3 ? можно интерпретировать как действие силы гравитации, которая стала расталкивающей. Этот факт сам по себе поразителен — гравитация издревле отождествлялась с тяготением. Правда, этим свойством отталкивания нельзя воспользоваться, как антигравитацией в фантастических романах. Поле с отрицательным давлением должно занимать огромное пространство, больше размеров горизонта, иначе на краях оно будет очень быстро падать и «выгорать», стремясь сжаться. К тому же поле должно быть весьма однородным внутри этого пространства, поскольку любые его перепады (градиент) дают вклад в притяжение. Чтобы расталкивание сработало, расширение должно быстро вынести все «края» пространства, занимаемого полем, за горизонт. Таким образом, расталкивающий эффект гравитации не может сделать ничего, кроме как создать огромную вселенную или раздуть уже существующую.

Теперь вспомним лямбда-член, введенный Эйнштейном в попытке стабилизировать нестационарную Вселенную. Он традиционно обозначается греческой «лямбда», откуда и получил свое название (альтернатива — космологическая постоянная), и фигурирует в уравнениях следующим образом:

R_{?? —} Rg_?? — 8??g_?? = 16?T_??/c⁴

Он тоже имел расталкивающий эффект и был по определению константой во всем пространстве. Уравнение Фридмана с лямбда-членом в отсутствие материи и в пренебрежении кривизной пространства выглядит так:

(?/a)² — 8?/3 · G? = 0,

где а — масштабный фактор, ? — его производная по времени. Уравнение Фридмана без лямбда-члена, но со скалярным полем, вошедшим в уравнение через тензор энергии-импульса:

(?/a)² = 8?G/3?

Да ведь это абсолютно то же самое, если в постоянно во времени и пространстве и если положить ? = ?! Так лямбда-член, забракованный Эйнштейном, вернулся в историю благодаря развитию теории поля, на сей раз в правую часть уравнения, через тензор энергии-импульса.

Каким будет решение уравнения Фридмана, приведенного выше? Конечно, экспонента: а = е^t, где t, напомним, — безразмерное время, выражаемое через обычное время, как t = t_rH; Н — постоянная Хаббла, которая в данном случае не меняется со временем: H = ?(8?G/3?).

Это решение носит имя де Ситтера, а умозрительная соответствующая ему вселенная называется «миром де Ситтера». Это несколько странный мир. Несмотря на экспоненциальный рост масштаба, в нем ничего не меняется. В нем нет глобальной выделенной системы отсчета (а в нашей Вселенной она есть — та, что связана с усредненным движением галактик и реликтовым излучением). Там непонятно, как определить причинно связанную область — горизонт. Более того, для мира де Ситтера можно преобразовать координаты так, что он будет вообще стационарным.

Странности этого мира снимаются малейшим отклонением от вакуумного состояния.

Если там есть хоть немного обычной материи, если скалярное поле и его плотность хоть чуть-чуть меняются во времени или пространстве, сразу экспоненциальное расширение становится реальным, хотя закон расширения будет чуть-чуть отличаться от экспоненты (см. врезку и рис. 13.1). Сразу исчезает стационарность, появляется выделенная глобальная система отсчета и многое другое.

Переход от чисто вакуумного состояния р = -? к близкому, например р = -0,99?, описан на врезке и проиллюстрирован на рис. 13.1. Переход достаточно плавен, но есть и серьезное отличие — где-то прошлом степенная зависимость упирается в ноль, а в будущем сильно отклоняется вниз. Кстати, теоретики рассматривают возможность р < -?. При этом нарушается так называемый принцип изотропной энергодоминантности, который кажется естественным, но напрямую ниоткуда не следует. Субстанция с таким уравнением состояния называется «фантомной материей», или «фантомной энергией» (второй вариант названия употребляется чаще). Подобный экзотический случай также проиллюстрирован на рис. 13.1: кривая в будущем отклоняется вверх от экспоненты и за конечное время уходит в бесконечность. Это так называемый «Большой разрыв» — страшилка, которую очень любят журналисты (Вселенную вплоть до атомов и нуклонов разорвет на элементарные частицы).

Фактически, сейчас мы наполовину раскрыли карты. Ускоренное расширение Вселенной — тот стержень, вокруг которого будет разворачиваться сюжет в следующей части. Но эта книга не детектив, и стержня мало — нужны еще конкретные сценарии с деталями, в которых может скрываться дьявол.

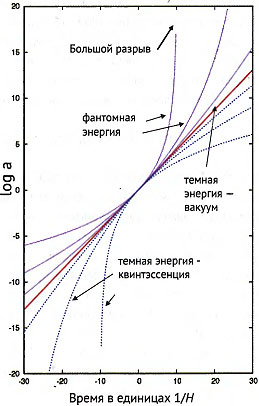
^{Рис. 13.1. Ход расширения пространства в зависимости от уравнения состояния содержимого вселенной. По горизонтали — время, выраженное в единицах 1/H₀, где H₀ — постоянная Хаббла в момент t = 0. По вертикали — десятичный логарифм масштабного фактора. Центральная красная линия — вакуумное уравнение состояния p = -?, ему соответствует точная экспонента. Снизу от нее идут кривые для р = -0,9?, -0,97?, -0,99? (в порядке приближения к экспоненте). Сверху, соответственно, идут кривые для р = -1,1?, -1,03?,-1,01?, что соответствует фантомной энергии}

Как решаются самые простые дифуры

Поскольку автор намерен помочь читателям (хотя бы тем, которые помнят что-нибудь о производных) всерьез разобраться, откуда берется ускоренное расширение Вселенной и как работает механизм космологической инфляции, на данной врезке подробно объяснено, откуда берутся приведенные в тексте решения уравнения Фридмана. Первое, что нужно знать, как выглядит производная степной функции у = х^? (? — любое фиксированное число). Вот так: dy/dx = ?х^?-1. Уравнение Фридмана для нулевой кривизны с учетом уравнения состояния и при использовании безразмерного времени (выраженного через постоянную Хаббла) выглядит так:

da/dt = a^?,

где а — масштабный фактор, а зависит от уравнения состояния вселенной. Решение ищется в виде

а = c(t+t₀)^?,

где с и t₀ — константы. Подставляем в уравнение Фридмана:

?c(t+t₀)^?-1 = c^?(t+t₀)^??

Понятно, что степени у переменной справа и слева должны быть равны:

?-1 = ??,

откуда

? = 1/(1-?)

и

с = (1/?)^?

На константу t₀ пока не обращаем внимания. Обратить внимание надо на случай a = 1, когда b обращается в бесконечность. В этом случае исходное уравнение превращается в

da/dt = а.

Это не только самое простое, но и самое знаменитое дифференциальное уравнение, описывающее размножение нейтронов при ядерном взрыве или бактерий в благоприятной среде. Его решение

a = e^t

основано на свойстве экспоненты оставаться самой собой при дифференцировании. Однако, предметом разбирательства остается переход между экспоненциальным и степенным решением. Он из соображений здравого смысла должен быть плавным, а из формул этого не видно. Здесь надо вспомнить про константу t₀. Добавим ее так, чтобы решение при t = 0 совпадало с экспоненциальным. Надо получить а = 1 при t = 0 и для этого взять t₀ = ?:

a = (1/?)^?(t + ?)^? = (1+t/?)^?

А теперь надо вспомнить определение числа е и убедиться, глянув в учебник или «Википедию», что последнее выражение при b стремящемся к бесконечности (что происходит, когда а стремится к 1 из-за того, что уравнение состояния вселенной стремится к вакуумному), стремится к e^t . Решения для значений а близких к 1 (или больших значений Ь) показаны в логарифмическом масштабе на рис. 13.1.