Беседа пятая
Беседа пятая
Любознайкин вносит некоторую ясность в размышления Незнайкина, приводя таблицу, в которой показаны схемы последовательного и параллельного соединений резисторов, катушек и конденсаторов и даны значения активных, реактивных сопротивлений для этих случаев соединений. Затем два друга подходят к проблеме резонанса — основного явления в радиотехнике. Любознайкин обращает внимание Незнайкина на некоторые моменты, которые облегчат в дальнейшем изучение радиоцепей.
МАТЧ — ИНДУКТИВНОСТЬ ПРОТИВ ЕМКОСТИ
Незнайкин. — Я очень рад встретиться опять с тобой. Наша последняя беседа оставила в моей голове такой туман, что я меньше, чем когда-либо, осмеливаюсь приступить к конструированию радиоприемника для твоей тетушки.
Любознайкин. — Это можно было предвидеть. Поэтому я сейчас покажу тебе таблицу (рис. 15), в которой приведены схемы последовательного и параллельного соединений резисторов, конденсаторов, катушек и даны определения величин для указанных случаев соединений, а также значения суммарной величины активного, индуктивного и емкостного сопротивлений.
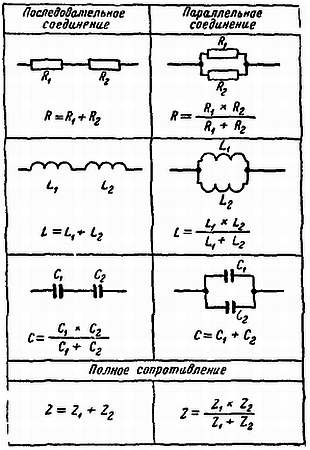
Рис. 15. Схемы последовательного и параллельного соединения сопротивлений, индуктивностей и емкостей.
Н. — Спасибо Это, без сомнения, поможет мне навести порядок в мыслях, а то ведь я от наших занятий стал плохо спать и это начинает внушать мне беспокойство
Л. — Неужели это радио, которое…
Н. — Ну да! Целую ночь я думал о том, что может получиться в результате последовательного соединения конденсатора и катушки Но, увы, я ничего не придумал.
Л. — Это неудивительно, потому что я ничего не говорил тебе еще об одном важном явлении. Сущность этого явления состоит в том, что хотя индуктивность и емкость являются сопротивлениями. Для переменного тока, эти сопротивления имеют как бы противоположные свойства. Индуктивность со свойственной ей инерцией задерживает появление тока (рис. 16) при приложении напряжения (в этом случае говорят, что происходит сдвиг по фазе и ток отстает от напряжения). Емкость обладает противоположным свойством: ток будет наибольшим в момент, когда конденсатор разряжен и, следовательно, напряжение равно нулю, по мере того как конденсатор заряжается и напряжение на нем возрастает, ток уменьшается.
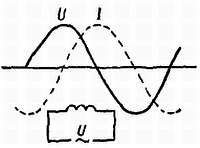
Рис. 16. Сдвиг фаз в цепи с индуктивностью: ток I отстает от напряжения U.
Н. — Да, ведь это верно! Когда мембрана выпрямлена, движется наибольшее количество воды (электронов), когда же она выгнута, движение прекращается.
Л. — Переводя на язык электротехники эту аналогию, можно сказать, что в цепи с емкостью ток смещен по фазе и опережает приложенное напряжение (рис. 17).
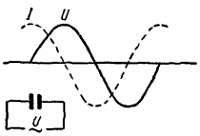
Рис. 17. Сдвиг фаз в цепи с емкостью: ток I опережает напряжение U.
Н. — Пусть так. Но что происходит, когда переменное напряжение приложено к емкости и индуктивности, соединенным последовательно? Я хотел бы все же уснуть сегодня ночью!
Л. — Ну, что же! В этом случае все зависит от соотношения между величинами индуктивного и емкостного сопротивлений. Если индуктивное сопротивление больше емкостного, то оно возьмет верх, и наоборот, так как емкостное сопротивление должно вычитаться из индуктивного. Ведь оно действует диаметрально противоположно.
Н. — Хорошо Позволь мне тогда задать тебе один из мучающих меня вопросов. Представь, что у меня есть конденсатор и катушка, включенные последовательно (рис. 18) Я прикладываю к ним переменное напряжение со все возрастающей частотой, что произойдет?
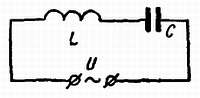
Рис. 18. Последовательное соединение емкости С и индуктивности L. На резонансной частоте сдвиг фаз и реактивное сопротивление уменьшаются до нуля.
Л. — Так ты же сам это знаешь очень хорошо.
Н. — Да, я знаю, что с возрастанием частоты индуктивное сопротивление увеличится, а емкостное — уменьшится. В этом случае неизбежно наступит момент, когда при некоторой частоте индуктивное и емкостное сопротивления будут одинаковыми. И так как одно должно вычитаться из другого, то общее реактивное сопротивление нашей цепи будет равно нулю?!
Л. — Ты рассуждаешь совсем неплохо. Однако ты забываешь, что простое активное сопротивление, не зависящее от частоты, останется все-таки в цепи. Но справедливо то, что при некоторой частоте емкостное и индуктивное сопротивления как бы взаимно компенсируются и в цепи в этот момент не будет сдвига фаз между напряжением и током.
КАПЛЯ, КОТОРАЯ РАЗБИВАЕТ РЕЛЬС
Н. — Значит, в этот момент сопротивление цепи достигнет минимума, а ток, следовательно, — максимума?
Л. — Конечно. Это состояние называется резонансом.
Н. — Правда, это похоже на историю с каплями воды, которые разбивают рельс?
Л. — Что ты еще выдумал?
Н. — Я где-то читал, что можно разбить стальной рельс, лежащий на двух опорах, если капать на его середину. Под ритмичным воздействием падающих капель рельс начинает вибрировать, и при определенной частоте падения капель вибрация становится такой сильной, что рельс может лопнуть.
Л. — Действительно, это пример механического резонанса. Точно так же цепь, состоящая из индуктивности и емкости, обладает собственной резонансной частотой, при которой сопротивление цепи становится очень малым, а колебания тока в ней — наибольшими. Это аналогично свойствам металлического бруска, который, обладая некоторой массой (эквивалент индуктивности) и некоторой упругостью (эквивалент емкости), имеет тоже резонансную частоту, для которой его вибрации становятся наибольшими. Первая капля создает очень слабое колебание в рельсе, вторая, попадая в нужный момент времени, увеличивает амплитуду колебаний и так далее.
Н. — Да, я теперь понимаю, что если капли падали бы немного быстрее или немного медленнее, то они не только не помогли бы колебаниям бруска, а даже помешали бы им. Но при резонансной частоте их действия складываются и брусок ломается, когда колебания становятся слишком сильными.
ВЕЧНОЕ ДВИЖЕНИЕ?..
Л. — Вернемся теперь, если хочешь, к электричеству. Представь, что у тебя есть заряженный конденсатор и что к его выводам ты присоединяешь катушку индуктивности (рис. 19). Что произойдет?
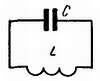
Рис. 19. Колебательный контур.
Н. — Я это знаю очень хорошо. Еще в последней нашей беседе мы изучили разряд конденсатора через сопротивление, а ведь катушка это все равно, что сопротивление. Следовательно, конденсатор разрядится через индуктивность… и все!
Л. — Вот как опасны слишком поспешные умозаключения! Ты забываешь, мой дорогой, что индуктивное сопротивление катушки немного особое, оно аналогично инерции. Электронам также трудно начать двигаться, как^ и остановиться. Значит, в момент, когда конденсатор разрядится, поток электронов будет еще продолжаться в том же направлении и…
Н. — … конденсатор снова зарядится, вероятно, изменив полярность. Но когда он снова зарядится?…
Л. — Он снова разрядится и так далее (рис. 20).
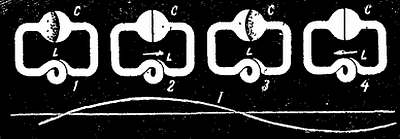
Рис. 20. Движение электронов в колебательном контуре в течение одного периода. В случаях 1 и 3 ток равен нулю, а напряжение на конденсаторе С максимально; в случаях же 2 и 4, наоборот, ток максимален, а напряжение на конденсаторе С равно нулю.
Н. — Значит, этому не будет конца? Достаточно зарядить конденсатор один раз, чтобы он, разряжаясь на катушку индуктивности, заряжался и разряжался вечно. Это же вечное движение?!
Л. — Не увлекайся! Наша цепь имеет активное сопротивление, и поэтому ток будет ослабевать, преодолевая это сопротивление. Вследствие этого в течение каждого колебания ток будет все меньше и меньше и, наконец, прекратится совсем.
Н. — Это похоже на колебания маятника, который, будучи выведен из состояния равновесия, качается до тех пор, пока вся энергия его не иссякнет из-за сопротивления воздуха.
Л. — Это самый классический пример, который приводится во всех учебниках по радиотехнике; может быть, ты легко догадаешься, какова же будет частота колебаний, образующихся в нашей цепи?
Н. — Я думаю, что электроны достаточно ленивы и будут следовать закону затраты наименьших усилий. Поэтому они будут колебаться на резонансной частоте — частоте, при которой кажущееся сопротивление цепи имеет наименьшее значение.
Л. — Все это именно так и происходит. В цепи, состоящей из индуктивности и емкости, называемой колебательным контуром, разряд конденсатора превращается в затухающие электрические колебания (переменный ток с уменьшающейся амплитудой), частота которых равна собственной или резонансной частоте колебаний контура (рис. 21).
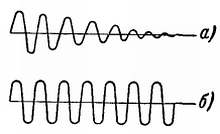
Рис. 21. Виды колебаний.
а — затухающие колебания; б — незатухающие колебания.
КОЛЕБАТЕЛЬНЫЙ КОНТУР И ВНЕШНЯЯ ЦЕПЬ
Н. — Существует ли способ постоянно поддерживать эти колебания?
Л. — Конечно. Можно получить колебания с постоянной амплитудой — незатухающие колебания, компенсируя потерю энергии за каждое колебание маленькой дозой энергии, добавленной от внешнего источника.
Н. — Я это понял и опять вспомнил часы. Ведь пружина или гири у стенных часов сообщают маятнику легкие толчки в такт с каждым колебанием.
Л. — Верно. Но в нашем случае надо колебательный контур LC связать с цепью, по которой проходит переменный ток, частота которого равна резонансной частоте колебательного контура. Связь может быть индуктивной (рис. 22, а) или же контур может быть включен непосредственно в цепь источника напряжения (рис. 22, б).
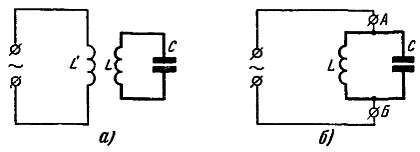
Рис. 22. Схемы питания колебательного контура LC.
а — индуктивное, б— непосредственное.
Н. — Я думаю, что в обоих случаях только ток резонансной частоты сможет усилить ток в колебательном контуре.
Л. — И ты не ошибаешься. Но вот, что еще важно — я прошу тебя обратить на это особое внимание! Когда колебательный контур включается в цепь (рис. 22,б), он представляет собой для тока на резонансной частоте значительное реактивное сопротивление.
Н. — Тогда… я больше ничего не понимаю! Ты же только что говорил, что для тока резонансной частоты реактивное сопротивление контура имеет наименьшую величину?!
Л. — Какой винегрет у тебя в голове!.. Пойми, наконец, что здесь мы имеем дело с двумя совершенно различными цепями. Одна, которую я рисую жирными линиями, это наш колебательный контур. Другая — это внешняя цепь, через которую проходит ток резонансной частоты.
Н. — Но откуда берется этот ток?
Л. — Ты это узнаешь позже — из антенны или цепи анода. В данный момент это несущественно… Внутри колебательного контура LC реактивное сопротивление действительно очень мало для тока с резонансной (собственной) частотой колебаний.
Рассмотрим теперь цепь, нарисованную тонкими линиями. Она служит для того, чтобы в течение каждого колебания тока передать в контур LC небольшое количество энергии, которое колебательный контур теряет за период каждого колебания. Таким образом, во внешней цепи может протекать только очень слабый ток. Отсюда следует, что колебательный контур по отношению к внешней цепи является большим сопротивлением.
Н. — Это очень сложно; однако мне кажется, что я понял.
Л. — И запомни еще очень важный вывод так как колебательный контур представляет собой большое сопротивление для резонансного тока внешней цепи, этот ток создаст (согласно закону Ома) очень большое переменное напряжение на зажимах А и Б колебательного контура (рис. 22, 6).
Н. — А что произойдет, если вместо тока резонансной частоты во внешней цепи будет протекать ток другой частоты?
Л. — В этом случае вынужденные колебания в колебательном контуре будут намного слабее, чем при резонансе. А сопротивление колебательного контура для нерезонансных частот будет значительно меньше. Таким образом, если во внешней цепи проходит одновременно много токов различной частоты, то только ток резонансной частоты создаст в колебательном контуре LC сильный ток, а на его зажимах — значительное напряжение. Таким способом ты можешь среди многих токов избрать один — ток резонансной частоты.
Н. — Я хотел бы спросить, от чего зависит резонансная частота, а также…
Л. — Я думаю, что на сегодня достаточно. Ты уже достиг насыщения и лучше остальное отложить на следующий раз. Мы сможем тогда покончить со всеми предварительными понятиями из электротехники и перейти непосредственно к радиотехнике.
