2. УПРАВЛЕНИЕ, СИГНАЛЫ, ИНФОРМАЦИЯ

2. УПРАВЛЕНИЕ, СИГНАЛЫ, ИНФОРМАЦИЯ

В этой главе мы поговорим о плотинах, шлюзах и термоэлектронной эмиссии, кострах на башнях и узелках на веревочках, объяснениях в любви, автопилотах и термостатах, двоичном коде, цифровых сообщениях и «плитках» информации, а также о многом другом, имеющем отношение к теме, указанной в заголовке.

Самое простое управление

Попробуйте отвернуть водопроводный кран и пустить холодную воду. Поворачиваем ручку крана, и из него льется струя холодной воды. Разве мы потратили много сил и энергии на поворот крана? Вовсе нет, а струя тем не менее сильная. А если мы откроем ворота шлюза в плотине? Хлынет вода, она приведет в действие гидроагрегат, и тысячи киловатт электроэнергии поступят в единую энергетическую сеть страны. Разве это мы затратили столько энергии? Вовсе нет, мы просто управляли шлюзом.

Водитель тяжелого грузовика слегка нажимает педаль акселератора, и многотонная махина резко набирает скорость. Не водитель же ее двигает! Разумеется, двигатель, водитель только управляет. Вы сами можете придумать тысячи примеров непосредственного управления — управления в его простейшем виде.

В школьном курсе физики изучают устройство радиолампы — катод, анод, управляющая сетка… Стоп! Опять управление! Кстати, если английское слово valve — лампа перевести дословно, то получим «клапан» или «кран».

Электронный клапан — триод.

Чем же этот «кран» управляет? Не потоком воды, разумеется, а потоком электронов. Накаленный катод лампы испускает электроны. В любом проводнике, а хорошим проводником электрического тока являются металлы, имеется так называемый электронный газ — множество свободных отрицательных электрических зарядов — электронов. Атомы металла объединены в общей кристаллической структуре твердого тела, причем внешние электроны атомов, слабее всех связанные со своим «родным» ядром, получают возможность переходить от атома к атому, т. е. блуждать по всему металлу, как киплинговская кошка, которая «гуляла сама по себе». Но покинуть металл электроны не могут, потому что они несут отрицательный заряд. Заряд одного электрона весьма мал, е = 1,6-10^-19 Кл. Тем не менее, если один электрон вырвется из металла, металл приобретет точно такой же по величине положительный заряд. Заряды противоположных знаков притягиваются (обратите внимание, как часто в жизни даже противоположные характеры тянутся друг к другу), и эти силы притяжения как бы втягивают электрон обратно в металл. Работа, которая требуется, чтобы удалить один электрон из металла, называется работой выхода. У разных металлов она разная, поэтому катод радиолампы стараются изготовить из металла с наименьшей работой выхода, например бария. Ну а если такой металл механически недостаточно прочен, его напыляют на более жесткий и тугоплавкий материал катода, обычно вольфрам. Когда катод разогревается током, проходящим по нити накала, до светло-красного каления, электроны в катоде двигаются быстрее. Они участвуют в тепловом движении — как бы сутолоке атомов, молекул, образующих нагретое вещество.

Пока вещество не расплавилось от нагрева, атомы остаются на своих местах в кристаллической решетке, они лишь колеблются все быстрее и быстрее. А вот электронам приходится туго. Как легкие мячики, их швыряют от атома к атому. И при достаточно сильном броске электрон приобретает кинетическую энергию, достаточную для совершения работы выхода. Таким образом, когда кинетическая энергия теплового движения электронов, пропорциональная температуре катода, становится сравнимой с работой выхода, происходит термоэлектронная эмиссия-излучение электронов нагретым катодом.

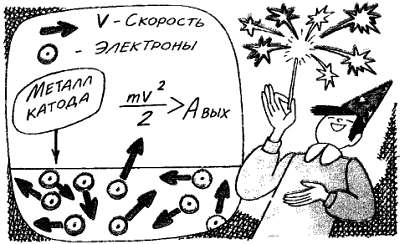
Термоэлектронная эмиссия.

Анод, заряженный положительно, притягивает и собирает вылетевшие из катода электроны. Несмотря на то, что в баллоне лампы глубокий вакуум, а катод и анод изолированы друг от друга, между этими электродами появляется электрический ток — направленное движение электронов, носителей заряда. Управляющая сетка, помещенная между катодом и анодом, служит тем самым «шлюзом», или «краном». Если сетка заряжена отрицательно по отношению к катоду, она отталкивает электроны, не пропуская их к аноду. По мере уменьшения отрицательного потенциала сетки все большая часть наиболее «шустрых» электронов (обладающих максимальной скоростью) проникает сквозь нее и попадает на анод. Анодный ток при этом увеличивается. При нулевом потенциале сетки почти все электроны достигают анода и анодный ток стремится к максимальному значению.

На сетке большое отрицательное напряжение.

Так действует электронная лампа — подобно вентилю, регулирующему поток воды из крана. Главным достоинством электронной лампы по сравнению с любыми другими вентилями и кранами является исключительно высокое быстродействие. Процесс включения и выключения анодного тока у современных ламп может длиться всего 10^-9 с, или 1 нс. Благодаря столь высокому быстродействию электронные лампы пригодны для усиления и генерирования колебаний очень высокой частоты, а также для создания быстродействующих управляющих, логических и вычислительных устройств. Правда, в последних из перечисленных областей применения электронные лампы практически полностью вытеснены полупроводниковыми элементами. Тем не менее с помощью электронной лампы можно проиллюстрировать процесс управления, поэтому мы рассмотрели ее так подробно.

Напряжение на сетке близко у нулю.

Не слишком простое, зато гораздо более эффективное управление

«Капитан взмахнул платком, наколотым на острие шпаги, и канониры тут же поднесли горящие фитили к запальным отверстиям пушек. Борт фрегата окутался густым пороховым дымом, а когда дым рассеялся под порывом свежего северо-западного ветра, люди с преследуемого галиона увидели «Веселый Роджер», взвившийся к ноку бизань-рея фрегата». Нам сейчас неважно, откуда взят этот отрывок, обратите внимание лишь на то, что капитан фрегата сам не прикасался к фитилям, не стрелял из пушек, он только взмахнул платком. И этот взмах послужил сигналом к выстрелу.

Управлял ли капитан атакой? Безусловно! Но управление происходило путем сигнализации, что очень существенно. Сигнализация может быть и многозвенной. Например, взмах платка на шпаге капитана видели только командиры батарей, они устно отдавали приказ канонирам (тоже сигнал), а те уже стреляли.

Один из способов сигнализации.

«Пушки с пристани палят, кораблю пристать велят». Разумеется, вы знаете, откуда эта строка. Здесь все происходило наоборот — выстрел пушки послужил сигналом к повороту корабля и предпринятого ряда действий для его швартовки у пристани. Здесь ясно усматривается управление кораблем посредством сигнализации. Классический пример передачи сигналов — костры на сторожевых башнях, зажигавшиеся при приближении неприятеля. Этот примитивный световой телеграф был очень распространенным средством связи и в древней Осетии, и на Руси, и в Литве и во многих других местах. Существенным недостатком такого телеграфа было лишь то, что днем его эффективность резко падала. Днем приходилось переходить на другой вид сигналов: либо разводить густой дым, либо махать с башни уже не платками, а большими флагами.

Кстати, флажный семафор на флотах с успехом просуществовал долгое время. Скорость передачи сообщений с помощью костров на башнях была удивительно велика, например для передачи сообщения вдоль всего балийского побережья требовалось менее часа. Ну а где же здесь управление? Да на всех этапах процесса передачи: маленькая искра, высеченная кремнем, управляла зажиганием большого огня костра, свет одного костра управлял зажиганием другого, и, наконец, свет последнего костра управлял, говоря современным языком, мобилизацией войск.

После второй мировой войны сформировалась новая наука кибернетика, занимающаяся вопросами управления. Ее создателем был Норберт Винер. Слово «кибернетика» — древнее, оно встречалось еще у Платона и обозначало искусство управлять кораблем. Известный французский физик Ампер, именем которого названа единица силы тока, называл кибернетикой науку об управлении государством.

В настоящее время кибернетика занимается математическим описанием процессов управления в машинах, механизмах, сложных, в том числе и электронных, системах, живых организмах. Кибернетика — наука об общих законах получения, хранения, передачи и переработки информации. Основной объект исследования так называемые кибернетические системы, рассматриваемые абстрактно, вне зависимости от их материальной природы. Примеры кибернетических систем — автоматические регуляторы в технике, ЭВМ, человеческий мозг, биологические популяции, человеческое общество и т. д.

Современная кибернетика состоит из ряда разделов, представляющих собой самостоятельные научные направления. Теоретическое ядро кибернетики составляют теория информации, теория алгоритмов, теория автоматов, исследование операций, теория оптимального управления, теория распознавания образов.

Разумеется, рассматриваемые кибернетикой процессы гораздо сложнее, чем, скажем, процесс управления водопроводным краном, хотя и он не так уж прост, как это может показаться на первый взгляд. Давайте откроем и закроем кран. Одновременно внимательно проследим за своими действиями. Открывая кран, мы смотрим на струю воды и отмечаем ее интенсивность. Отвинчивать рукоятку крана мы прекратим, когда решим, что поток воды достаточен. Вы заметили, что имеется обратная связь: интенсивность струи воды влияет на принятие нами решения открывать кран дальше или нет.

Подобные процессы происходят и в любой другой системе управления. Органы, планирующие выпуск и распределение товаров, обязательно должны иметь информацию об их наличии в магазинах, на складах, у населения. Иначе может случиться, что будет их избыток в одном месте и недостаток в другом.

На старых самолетах при вхождении в пике пилот, отклоняя от себя штурвал, или ручку управления, должен был внимательно следить за положением самолета относительно горизонта, чтобы пикирование не превратилось в отвесное падение или самолет не вошел в «штопор». На современных самолетах имеются приборы (гировертикали или гирогоризонты), автоматически определяющие положение фюзеляжа самолета в пространстве. Сигналы этих приборов воздействуют на рули управления таким образом, чтобы выдерживался заданный летчиком угол пикирования. Комплекс устройств, обеспечивающих автоматическое ведение самолета с заданными скоростью, курсом и высотой, называют автопилотом. Примерная структурная схема устройства автопилота, обеспечивающего регулирование только одного параметра, например курса самолета, показана на рисунке.

Автопилот.

При появлении сигнала (летчик повернул штурвал на некоторый угол) система управления заставляет отклоняться рули самолета, и его курс изменяется. Датчик положения вырабатывает сигнал, соответствующий новому курсу, а сравнивающее устройство контролирует, достиг ли этот сигнал требуемого значения, и, если нужно, вносятся коррективы. Как только самолет лег на нужный курс, сигнал обратной связи, вырабатываемый сравнивающим устройством, прекращает действие сигнала управления и система управления устанавливает рули в нейтральное положение. Особое значение имеет обратная связь для автоматического поддержания заданного курса. Допустим, что никакого сигнала управления от летчика не поступало, но курс самолета несколько изменился (подул боковой ветер или на пути попалась «воздушная яма»). Датчик положения немедленно отреагирует на изменившееся направление полета, и сравнивающее устройство выработает сигнал ошибки. По цепи обратной связи он поступит в систему управления, а она повернет рули самолета и скорректирует курс.

Другой пример автоматическое устройство для поддержания заданной температуры — термостат. Он используется и в аппаратуре для тонких биохимических исследований, и в высокостабильных кварцевых генераторах, и в инкубаторах для выведения цыплят.

Температура внутри устройства контролируется датчиком, например терморезистором. Его сигнал сравнивается с опорным, задающим нужное значение температуры. Если температура понижается, сопротивление терморезистора возрастает и сравнивающее устройство вырабатывает сигнал обратной связи, управляющий регулятором тока, который, в свою очередь, включает нагреватель.

Но как только температура объекта достигает заданной, нагреватель отключается. Как видим, здесь тоже имеет место управление с обратной связью: регулируемый параметр управляет работой системы управления.

Устройство термостата.

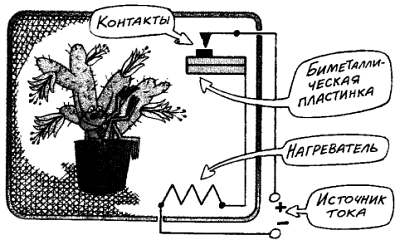
Простейший термостат.

Какова же роль электроники в описанных процессах? Самая непосредственная. Здесь мы имеем дело с сигналами управления, датчиков, обратной связи. Они могут передаваться в различной форме, но главное-чтобы их можно было легко и быстро обработать. Для этого на данном этапе развития науки и техники лучше всего подходят электрические сигналы. Следовательно, все устройства и блоки, показанные на структурных схемах, должны быть электронными. Конечно, в ряде случаев пригодны и очень простые устройства, не содержащие электронных схем. Например, простейший регулятор температуры содержит лишь биметаллическую пластинку с контактами и спираль нагревателя. Благодаря разным коэффициентам линейного расширения металлов, из которых изготовлена пластинка, при изменениях температуры она изгибается, замыкая контакты при остывании и размыкая при нагреве. Точность регулирования в таком устройстве невысока и составляет единицы градусов. Как правило, электронный регулятор температуры содержит интегральную микросхему-операционный усилитель, усиливающий слабый сигнал датчика и сравнивающий его с опорным, а также мощные транзисторы и тиристоры, управляющие током нагревателя. В результате получают точность поддержания температуры до сотых долей градуса, а при необходимости и еще выше.

Итак, управление осуществляется посредством сигналов.

Посигнализируем сигналами о сигналах

Я рад, что редактор после долгих споров пропустил этот подзаголовок, не выдерживающий никакой критики с литературной точки зрения. Следовало бы сказать проще: «Поговорим о сигналах». Но само слово «сигнал» имеет общий корень с английским sign, что можно перевести как знак, обозначение. Написанное слово означает некоторое понятие и, таким образом, тоже является сигналом. Ну а передача сигналов, хотя бы и на бумаге, — это сигнализация. Поэтому посигнализируем немного словами-сигналами на тему о сигналах.

Сигналы, передаваемые в электрической форме, обладают множеством достоинств. Во-первых, не требуется движущихся механических устройств, медленных и подверженных поломкам. Во-вторых, скорость передачи электрических сигналов приближаемся к максимально возможной скорости света. Наконец, в-третьих, электрические сигналы легко обрабатывать, сравнивать и преобразовывать с помощью электронных устройств, отличающихся чрезвычайно высоким быстродействием. Вот почему электрический телеграф, изобретенный в первой половине прошлого века, прочно удерживает свои позиции и не уступает их до настоящего времени в почтовых ведомствах всех стран. Телефон, созданный во второй половине прошлого века, основан на преобразовании механических колебаний частиц воздуха в электрические сигналы. Радио это тоже передача сигналов, но уже не с помощью электрического тока, текущего по проводам, а с помощью электромагнитных волн, не требующих для распространения какой-либо среды. Радиоволны лучше всего распространяются в космосе, несколько хуже — в атмосфере Земли и совсем плохо — в толщах суши и океанов (там они просто поглощаются, проникая лишь на ограниченную глубину порядка длины волны). Радиоволны — истинные приверженцы свободы и простора; вдали от поглощающих материальных тел, в безбрежных просторах открытого космоса они живут вечно. Я не утрирую. Совсем недавно открыто реликтовое (древнее) излучение, существующее столько же лет, сколько лет и нашей вселенной. Об этом я еще расскажу позже, а сейчас вернемся к сигналам, не внеземных цивилизаций, конечно (они пока не обнаружены, хотя исследования в этом направлении проводятся), а к нашим обычным, земным.

Сигнал в его простейшей форме может принимать два дискретных и вполне определенных значения. Например, на сигнальной башне огонь есть — огня нет. Яркость огня никакого значения не имеет, лишь бы огонь было ясно видно.

В телеграфной азбуке Морзе сигнал тоже может принимать только два дискретных значения: пищит-не пищит, есть ток — нет тока, передатчик излучает электромагнитную волну — не излучает.

Кстати говоря, не бывает сигнала, принимающего только одно дискретное значение. Например, если костер на башне жгут постоянно или не зажигают вовсе, то нет никакой возможности узнать, когда же вторгся неприятель.

Во всех разобранных случаях использован простейший двоичный или бинарный код. Наличие сигнала удобно обозначать символом «1», отсутствие «0». Сигналы, передаваемые двоичным кодом, удобны во многих отношениях. Как и любые цифровые дискретные сигналы, их можно регенерировать, т. е. восстановить, воссоздать их форму, искаженную помехами. Костер, загоревшийся на двенадцатой сигнальной башне, является копией первого костра, зажженного на первой башне, и несет он абсолютно тот же смысл, абсолютно то же сообщение, обозначенное нами символом «1». Не имеет значения, хорошо виден огонь или не очень, что форма костра совсем другая — это влияние помех, которое не сказывается на принятии наблюдателем решения, что костер на предыдущей башне горит. Следствием этого будет регенерация сигнала — зажигание костра на следующей башне.

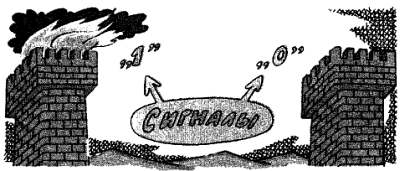
Сигналы.

Так же легко регенерировать код Морзе. В простейшем случае это делает телеграфист — принимает на слух сообщение и отстукивает его ключом дальше по линии. Регенератором служит и телеграфное реле. При наличии посылки тока его контакты замыкаются и формируют новую, уже очищенную от помех посылку тока. Надо ли говорить, что электромеханические реле заменяются более надежными и быстродействующими электронными.

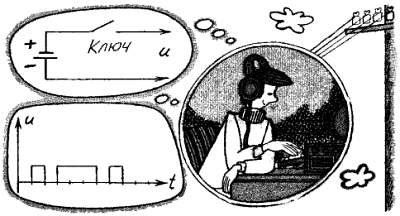
Телеграфные сигналы.

Другое достоинство двоичных цифровых сигналов заключается в том, что они требуют минимального отношения сигнал-помеха в канале связи. Поясним, что что такое. Когда дозорный смотрит на далекую сигнальную башню, ему мешают свет зари, мерцающий свет звезд, расположенных низко над горизонтом, зажигаемый кем-нибудь «посторонний» огонь. Для надежного распознавания полезного сигнала, т. е. света сторожевого костра, надо, чтобы его яркость была больше яркости посторонних помех. Как говорят связисты, отношение сигнал-помеха должно быть больше единицы.

То же и в электрическом телеграфе. Провода линии связи «гудят» вследствие атмосферного электричества, электризации трением от ветра, из-за случайных полей геомагнитного происхождения в телеграфных проводах наводится некоторое напряжение помех. Подземные кабели в этом отношении несколько лучше, но они дороже и все равно полностью не избавляют от помех. Даже если нет внешних наводок, тепловое движение электронов в проводнике создает хаотически изменяющееся случайное напряжение так называемый тепловой шум. Кстати, если это напряжение усилить и подвести к громкоговорителю, мы услышим шум, напоминающий шум примуса, паяльной лампы или сильного дождя. Зачем далеко ходить за примерами, каждый из нас слышал шум и помехи в телефонной трубке! Для надежной регистрации телеграфных посылок их напряжение должно быть больше напряжения шума и помех. Отношение сигнал-шум или сигнал-помеха, требуемое для получения заданного качества связи, оказывается наименьшим при использовании двоичных цифровых сигналов, поэтому говорят, что линии связи, использующие цифровой двоичный код, обеспечивают наибольшую помехоустойчивость.

Другой вид сигналов — аналоговые. Типичный пример — напряжение, развиваемое микрофоном при разговоре перед ним, пении или игре на музыкальных инструментах. Давление воздуха при звучании источника изменяется в небольших пределах относительно нормального атмосферного. Мембрана микрофона, прогибаясь под действием звукового давления, создаст некоторое напряжение на выводах звуковой катушки микрофона. Это напряжение прямо пропорционально звуковому давлению, т. е. изменяется аналогично ему, откуда и происходит название «аналоговый сигнал».

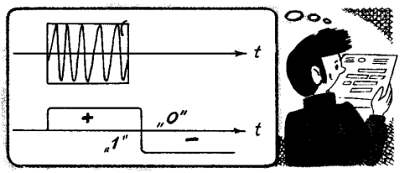
Дискретные сигналы.

Аналоговые сигналы до сих пор используют в телефонной связи, радиовещании и телевидении. Это проще технически, да и история развития радиотехники сложилась так, что первыми стали применяться аналоговые сигналы. Это никоим образом не относится к телеграфу, где всегда господствовала цифра. При передаче аналоговых сигналов требуется значительно большее отношение сигнал-шум, чем при передаче двоичных цифровых сигналов. Пробовали разговаривать в метро? Шум поезда, отражаясь от стенок туннеля, приобретает большую интенсивность. Шум поезда — это помеха. Приходится напрягать голос, чтобы речь была разборчивой.

Мощность громких звуков человеческого голоса в 10000 раз превосходит интенсивность слабых звуков. И это при обычном разговоре. Но слабые звуки не должны маскироваться шумом, чтобы их тоже можно было разобрать. Вот почему приходится напрягать голос в метро, вот почему приходится на аэродроме кричать в ухо собеседнику, когда реактивный лайнер, ревя двигателями, подруливает к аэровокзалу. Для хорошего качества речи, передаваемой по телефону, необходимо обеспечить отношение сигнал-шум по напряжению примерно 100, или 40 децибел (дБ). (Разница уровней в децибелах есть двадцать десятичных логарифмов отношения напряжений.) Опытные радисты могут разобрать речь при отношении сигнал-шум около десяти, но при условии, что передаваемый текст знаком и привычен.

Большим недостатком аналоговых сигналов является и то, что их нельзя регенерировать, поскольку нам не известна их форма (известный сигнал и передавать незачем!). Когда еще лет десять назад вы разговаривали по междугородному телефону, замечали ли, насколько плохим было качество связи? Объяснялось это тем, что слабый речевой сигнал при передаче по проводной телефонной линии необходимо периодически усиливать, скажем через каждые 100 или 200 км. Гудят провода, шумят усилители, и каждый из этих источников помех все больше и больше искажает передаваемый сигнал.

Аналоговые сигналы.

Нельзя ли как-нибудь использовать двоичный канал для передачи речи, спросит читатель? Конечно, можно! И такой способ передачи широко используется в настоящее время. Первое, что в этом случае необходимо сделать, — это преобразовать аналоговый речевой сигнал в цифровой код. Затем цифровой сигнал передается по линии связи и регенерируется на каждом из промежуточных усилительных пунктов. Помехи при этом устраняются. А перед подачей в телефонную трубку цифровой сигнал снова превращают в аналоговый. Подобные системы уже внедрены на некоторых междугородных линиях связи. Не обошлось и без курьезов. При первых испытаниях цифровой линии стоило одному из корреспондентов замолчать, как другой принимался кричать: «Алло, алло!», думая, что связь оборвалась. На самом деле он просто не слышал привычного шума линии в паузах речи — столь чистой оказалась передача. Пришлось нарочно добавить немного шума к сигналу на каждом из оконечных пунктов!

Так что же переносят сигналы?

Надеюсь, что читатель сам сможет ответить на этот вопрос. Любой сигнал, будь то свет костра, телеграмма, код Морзе написанный текст и т. д., несет какое-либо сведение, или сообщение! Одним словом — информацию. Таким образом, сигнал есть средство передачи информации.

Любой переданный сигнал переносится либо энергией, либо веществом. Иначе и быть не может, ведь наш мир материален. Это либо акустическая волна (звук), либо электромагнитное излучение (свет, радиоволна), либо лист бумаги (написанный текст), либо каменная скрижаль с выбитыми на ней магическими знаками. Но ни переданная энергия, ни посланное вещество сами по себе никакого значения не имеют, они служат лишь носителями информации. По мере удаления от передатчика поток энергии становится все слабее и слабее. Это тоже не имеет значения до тех пор, пока превышение сигнала над шумом достаточно для приема информации. Когда Москва передает по радио последние известия, одну и ту же информацию получает и подмосковный радиослушатель в г. Долгопрудном и уральский радиослушатель из Нижнего Тагила. Но поток энергии радиоволн в Нижнем Тагиле в тысячи раз меньше, чем под Москвой. Истрепанная книжка, если в ней нет вырванных страниц, несет ровно столько же информации, сколько такай же новая.

Каменная скрижаль весом в три тонны несет столько же информации, сколько ее хороший фотоснимок в археологическом журнале. Следовательно, мощность сигнала, так же как и вес носителя, никак не могут служить оценкой количества информации, переносимой сигналом. Как же оценить это количество?

Во время второй мировой войны подобные вопросы не на шутку заинтересовали шифровальщика при одном из штабов американских войск в Европе К. Шеннона. Упорство в достижении поставленной цели часто приносит успех, и после войны К. Шеннон защитил докторскую диссертацию, став основоположником новой науки — теории информации. В 1948–1949 годах увидели свет его статьи «Математическая теория связи» и «Связь в присутствии шума».

Любое сообщение можно свести к передаче чисел. Пылкий влюбленный, находясь в разлуке с объектом своей любви, посылает телеграмму: «Любишь?». В ответ приходит не менее лаконичная телеграмма: «Да!». Сколько информации несет ответная телеграмма? Альтернатив здесь две — либо Да, либо Нет. Их можно обозначить символами двоичного кода 1 и 0. Таким образом, ответную телеграмму можно было бы закодировать единственным символом «1». Выбор одного нз двух сообщений («Да» или «Нет», «1» или «0») принимают за единицу информации. Она названа «бит» — сокращение от английских слов binary digit, что означает двоичная цифра. Таким образом, ответная телеграмма несла всего 1 бит информации. А вопрос ценности этой информации для получателя-это уже из иной области.

Однако только что данное определение единицы информации слишком упрощено. Если влюбленный уверен в положительном ответе, то ответ «Да» не даст ему почти никакой новой информации.

Информация измеряется в битах.

То же самое относится и к безнадежно влюбленному, уже привыкшему получать отказы. Ответ «Нет» также принесет ему очень мало информации. Но внезапный отказ уверенному влюбленному (неожиданное огорчение) или ответ «Да» безнадежно влюбленному (нечаянная радость) несут сравнительно много информации, настолько много, что радикально изменяется все дальнейшее поведение влюбленного, а может быть, и его судьба! Таким образом, количество информации зависит от вероятности получения данного ответа.

Лишь при равновероятных ответах ответ «Да» или «Нет» несет 1 бит информации. Общая формула для подсчета количества информации, содержащегося в сообщении а, выглядит гак

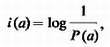
где Р(а) — вероятность появления данного (дискретного) сообщения а.

Обратите внимание, что для абсолютно достоверного события P(а) = 1 (событие обязательно произойдет, поэтому его вероятность равна единице), при этом количество информации в сообщении о таком событии i(а) = 0. Чем невероятнее событие, тем большую информацию о нем несет сообщение.

Но зачем в приведенной формуле использована логарифмическая функция? Нельзя ли проще? Нет, проще не получается. Информация, содержащаяся в двух независимых сообщениях a₁, и а₂, должна быть равна сумме информации, содержащихся в каждом из сообщений: i(a₁,a₂) = i(a₁) + i(a₂). Логичное требование, не правда ли? Но вероятность того, что источник пошлет оба эти сообщения, одно за другим, равна произведению вероятностей появления каждого из сообщений: P(a₁,a₂) = Р(а₁)·Р(а₂). Как известно, при умножении двух величин их логарифмы складываются. Поэтому и количество информации должно выражаться логарифмической функцией.

Ввиду широкого использования двоичных сигналов в вычислительной технике и связи, чаще всего используют логарифм по основанию два. При этом количество информации оказывается выраженным в битах. Если в примере с влюбленными вероятность ответов «Да» и «Нет» одинакова и, следовательно, составляет 0,5, то количество информации в одном ответе составляет 1 бит.

Ну а что если выбор надо осуществить не из двух сочетаний, а из множества? У древних индейцев Центральной Америки существовало узелковое письмо. Писали, завязывая узелки на веревке. Совершенно очевидно, что при таком способе письма можно использовать двоичный код: есть узелок в данном месте единица, нет узелка — нуль. Если на каждом сантиметре длины веревки разместить по узелку, то метровая веревка будет нести 100 бит информации. Согласитесь, это не так уж мало.

В одном романе Жюля Верна собака, увидев игрушечные кубики с буквами, выбрала из них вполне определенные, с буквами, которые составили имя ее пропавшего хозяина, чем и приоткрыла завесу над тайной его исчезновения. Здесь мы видим выбор определенных знаков из 26, составляющих английский алфавит.

Еще один пример, но теперь из реальной жизни — 1943 год, англо-американские войска готовятся к высадке на итальянский остров Сицилию, занятый фашистскими войсками. В это время в одной из тюрем США сидел очень влиятельный гангстер Лучано, выходец из Сицилии. Американская разведка, пользуясь всяческими средствами, вступила с ним в сговор, пообещав досрочное освобождение. В результате с самолета над Сицилией был сброшен вымпел — шелковый платок с вышитой на нем буквой L. Сицилийские мафиози, в то время не ладившие с немецко-фашистскими оккупантами, прекрасно поняли смысл сообщения: Лучано за союзников! Эффект был поразителен — американская армия практически не понесла потерь при освобождении Сицилии, так как мафиози основательно помогли ей, начав партизанскую войну против немцев.

Сейчас нас интересует не значимость для истории сообщения на вышитом платке, а лишь количество переданной информации. В английском алфавите 26 букв, добавим еще служебные знаки препинания — всего 32 знака. Значит, осуществлялся выбор одного из 32 знаков. Пример характерен тем, что при передаче любых телеграмм, на любом языке в приемном устройстве происходит выбор одной буквы из алфавита, который чаще всего содержит 32 знака. Если вероятность появления каждого из знаков одинакова и, следовательно, составляет 1/32, то при передаче одного знака сообщается log₂32 = 5 бит информации. Ту же цифру мы можем получить и иным способом. Перенумеруем все буквы алфавита по порядку.

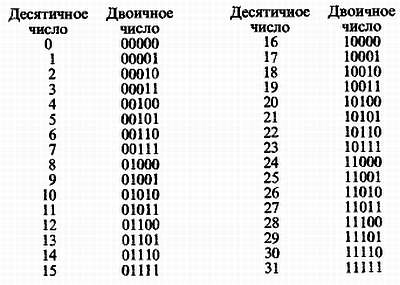
Буква L стоит на двенадцатом месте, и ее порядковый номер будет 12. Теперь для выбора этой буквы достаточно передать ее порядковый номер. Число 12, выраженное в двоичном коде, выглядит как 01100. Для передачи любого из 32 чисел двоичным кодом нужно пять разрядов, а любого из N чисел log₂N. Вы еще не умеете переводить числа из десятичного исчисления в двоичное и обратно?

Научитесь, это не так уж сложно! Вам поможет приведенная таблица и простое правило: последний разряд двоичного числа дает единицы (2⁰), предпоследний — двойки (2¹), третий разряд справа — четверки (2²), четвертый восьмерки (2³), и т. д. Обозначив символы двоичного кода (1 и 0) в последнем разряде х₁, в предпоследнем х₂ и т. д., получим простую формулу для структуры двоичного числа:

N = х₁·2⁰ + х₂·2¹ + х₃·2³ +…

Для передачи любого числа от 0 до 31 необходимо пять двоичных разрядов, или 5 бит информации. Таким образом, сообщение гангстера Лучано мафиози содержало 5 бит информации.

В народном хозяйстве необходимо передавать значительно больше информации. Не вызовет удивления, например, такая телеграмма, переданная работником снабжения: «В феврале на Чукотку поступило 10 000 грампластинок». Информация здесь такова: во-первых, февраль. Надо думать, поставки товаров подобного рода производятся ежемесячно, поэтому февраль надо обозначить цифрой 2. Отсюда определяем число двоичных разрядов, необходимых для передачи номера месяца: 4 (2⁴ = 16, имеется некоторая избыточность информации). Далее необходимо ввести код Чукотки. Пусть соответствующая организация поставляет товары в 120 краев и областей, причем Чукотке ввиду ее удаленности присвоен последний номер. Тогда для передачи кода Чукотки (120) потребуется 7 двоичных разрядов (2⁷ = 128). После кода области надо указать код товара. Если всего поставляется, например, 512 наименований товаров, то для обозначения грампластинок, скажем № 384, потребуется 9 разрядов (2⁹ = 512). И наконец, число грампластинок 10000 в двоичном коде займет 14 разрядов. Получаем следующую таблицу:

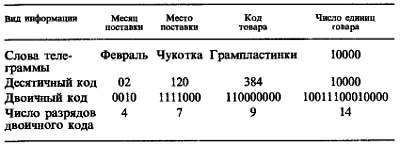
Полное сообщение требует 34 двоичных разряда. Спереди обычно добавляют несколько разрядов служебной информации адрес, знак начала сообщения и т. д. Последовательность кодов и число разрядов каждого кода, указанные в таблице, должны быть и у отправителя, и у получателя сообщения, чтобы они имели возможность закодировать и раскодировать телеграмму. На линии связи эти процессы автоматизированы, соответствующие устройства называют кодерами и декодерами.

В книгах про разведчиков подобные таблицы называются шифрами и ключами к шифрам, скажет сообразительный читатель, и будет совершенно прав. Надеюсь, что наиболее юные и энергичные из читателей придумывают свои собственные шифровальные таблицы для игры в разведчиков, и их шифры, особенно представленные в двоичном коде, вряд ли расшифрует «неприятель». Итак, мы научились представлять информацию в цифровой форме и определять ее объем. А как быть с аналоговыми сигналами? Раньше их обрабатывали в аналоговой форме, теперь все чаще преобразуют в цифровую.

Вспомним автопилот самолета, который мы уже рассматривали, и попробуем сконструировать простейший датчик углового положения фюзеляжа. Возьмем отвес — жесткий стержень с грузом на конце, закрепленный на горизонтальной оси 0. Верхний конец стержня соединим с подвижным контактом потенциометра R, а к крайним выводам потенциометра подключим источники напряжения -10 и + 10 В. Если фюзеляж самолета находится в горизонтальном положении, подвижный контакт будет в середине резистивной подковки потенциометра, а потенциал на нем U обратится в нуль.

Стоит самолету наклониться вперед, скажем войти в пике, движок потенциометра переместится влево по подковке и потенциал U станет отрицательным. Если же носовая часть самолета будет направлена вверх, потенциал U станет положительным. Пусть при наклоне фюзеляжа на угол ± 20° потенциал U изменяется от + 10 до —10 В. Крутизна характеристики преобразования угол напряжение для такого датчика составит 0,5 В на градус. Таким образом мы получим аналоговый сигнал углового положения самолета. Для преобразования этого сигнала в цифровую форму необходимо задаться шагом дискретизации — минимальным изменением напряжения, соответствующим изменению цифрового кода на единицу.

Если в нашем простейшем случае достаточна точность 1°, то шаг дискретизации будет равен 0,5 В. Число шагов дискретизации, на которое изменилось напряжение U, и будет являться углом наклона фюзеляжа, выраженным в градусах. Его значение можно представить и двоичным кодом, как это показано на рисунке.

Датчик углового положения.

Дискретизация по уровню.

Для преобразования аналоговых величии в цифровой код служат специальные электронные устройства — аналого-цифровые преобразователи (АЦП). Полученный цифровой код углового положения фюзеляжа поступает в цифровой процессор, выполняющий функции и сравнивающего устройства, и системы регулирования (посмотрите схему на стр. 19). Сюда же поступают сведения и о положении самолета в других плоскостях пространства, и о положении рулей. Процессор вырабатывает сигнал, управляющий рулями. При цифровой обработке информации можно получить значительно большую точность регулирования и управления. Этим и объясняется широкое применение цифровой техники в системах управления.

С какой точностью, например, можно измерить напряжение с помощью обычного стрелочного прибора? Лучшие лабораторные магнитоэлектрические приборы с зеркальной шкалой обеспечивают точность отсчета не более 0,2 %, что составляет 2·10^-3. В то же время цифровые вольтметры могут иметь пять-шесть разрядов, что обеспечивает точность измерений на два-три порядка (в 100… 1000 раз) выше. Но вернемся к проблемам связи, ведь мы так и не закончили разговор о передаче телефонных сигналов цифровым кодом.

Разговор по телефону в цифрах

Несколько лет назад мне довелось пройти на гидрографическом судне от Владивостока до Петропавловска-Камчатского. Естественно, что из каждого порта я звонил домой, в Москву, чтобы справиться о делах и здоровье близких. Владивосток был еще связан с Москвой старой системой аналоговой телефонной связи. Часа три приходилось ждать, пока телефонистки соединят линию. Наконец, еле-еле, сквозь шумы и трески послышался голос жены. Совсем иная картина была в Петропавловске. Там действовала цифровая телефонная связь. Прямо из кабины телефона-автомата можно набрать код Москвы, затем две-три служебные цифры и нужный номер в Москве. Весь процесс занял не более минуты, причем более половины этого времени ушло на то, чтобы разобраться в правилах пользования автоматом, вывешенных в кабине: какие набирать цифры, каких ждать гудков и т. д. Слышно было лучше, чем когда я звонил соседу по дому в Москве, так же хорошо слышали и меня, а помех практически не было. Надо ли говорить, что после состоявшегося разговора я стал ярым приверженцем цифровой телефонной связи.

Так как же обычная человеческая речь превращается в поток цифр, ведь на выводах микрофона имеется быстро изменяющийся речевой сигнал (как показано на рисунке)? А вот как. Берутся отсчеты, т. е. значения этого сигнала через равные промежутки времени ?. Интервал ? должен быть настолько мал, чтобы речевой сигнал не успевал намного измениться между отсчетами. Этот интервал часто называют временным шагом дискретизации или интервалом Найквиста. Минимальную частоту взятия отсчетов, т. е. величину, обратную временному шагу дискретизации, определяет теорема В. А. Котельникова (академика, основателя теории помехоустойчивости систем связи). Частота отсчетов должна быть вдвое больше самой высокой частоты звукового спектра. В телефонии принято передавать частоты только до 3400 колебаний в секунду, т. е. до 3,4 кГц. При этом разборчивость речи еще очень хорошая. Значит, частота взятия отсчетов должна быть не менее 6800 в секунду, или 6,8 кГц. Процесс взятия отсчетов называют дискретизацией по времени.

Для цифровой оценки отсчетов нужен следующий процесс — дискретизация по уровню. Каждый отсчет можно представить числом, соответствующим значению отсчета звукового напряжения. Например, если звуковое напряжение измерять в милливольтах, то число целых милливольт и будет отсчетом, а один милливольт — шагом дискретизации по уровню. Ошибка квантования но уровню в данном случае не превзойдет половины шага квантования, т. е. 0,5 мВ. Отношение максимальной амплитуды звукового напряжения к шагу квантования даст максимальное число, которое можно получить при отсчетах. Оно определяет динамический диапазон передаваемого сигнала. Для передачи телефонной речи с удовлетворительным качеством достаточен динамический диапазон (отношение максимального уровня сигнала к минимальному) 30… 35 дБ, что соответствует числу шагов квантования при отсчетах 30. Для передачи одного отсчета двоичным кодом в этом случае достаточно In ₂30 ~= 5 разрядов. Для хорошей передачи музыки это число, число шагов квантования по уровню, должно быть не менее 10000, что соответствует динамическому диапазону 80 дЬ. В этом случае для передачи одного отсчета потребуется log₂10000 ~= 14 разрядов.

Преобразование аналогового сигнала в цифровой.

Наконец мы можем оценить поток информации при телефонном разговоре. Полагая полосу звуковых частот равной 3,4 кГц и частоту взятия отсчетов 6,8 кГц, получаем количество отсчетов в секунду 6800. При 30 шагах квантования по уровню каждый отсчет занимает 5 разрядов. Следовательно, в секунду передается 34000 двоичных разрядов, или бит информации. Скорость передачи информации, измеренную в битах в секунду, можно выразить формулой

С = 2F·log₂N,

где F — наивысшая частота звукового спектра; N — число уровней квантования.

Перейдя на цифровую передачу, мы существенно улучшили качество связи. Но не даром же это досталось! Чтобы передать цифровой сигнал со скоростью 34 кбит/с, нужна полоса частот, пропускаемых каналом связи, не менее 34 кГц. А теперь вспомним, что для передачи обычного аналогового телефонного сигнала требуется полоса частот всего 3,4 кГц. Таким образом, цифровые системы связи оказываются широкополосными. Происходит как бы обмен полосы частот на отношение сигнал-шум, но обмен достаточно выгодный. Расширяя полосу частот в десять раз при переходе к цифровой передаче, мы намного снижаем допустимое отношение сигнал-шум, или сигнал-помеха, в канале связи, и это при общем существенном улучшении качества.

Скорость передачи 34 кбит/с достаточно большая, но надо учесть, что при телефонном разговоре с речью как таковой передаются и интонации голоса, и эмоциональная окраска, что хорошо знают все, кто разговаривал друг с другом по телефону, да и не только по телефону. Телеграф, к сожалению, таких нюансов передать не может. Давайте ради интереса оценим, каков будет поток информации, если телефонный разговор заменить телеграфной передачей того же текста. При среднем темпе речи человек произносит 1… 1,5 слова в секунду. Каждое слово состоит в среднем из пяти букв. А для передачи телеграфом одной буквы требуется 5 бит (считаем, что алфавит содержит 32 знака). Перемножив все эти числа, получим скорость передачи телеграфной информации, соответствующей тексту телефонного разговора в реальном масштабе времени, С ~= 30… 40 бит/с. Это почти в тысячу раз меньше! Вот во что обходятся связистам эмоции и интонации телефонных разговоров. Одна и та же междугородная линия связи может пропустить, скажем, 16 телефонных каналов или несколько тысяч телеграфных!

Но подождите, то ли еще будет, когда мы перейдем к телевидению! Там ведь надо передавать еще и движущиеся изображения.

Посмотрим, какой результат мы получили, положив скорость передачи в телефонном канале равной 30 кбит/с, а в телеграфном 30…40 бит/с? Ведь мы предположили, что каждый последующий отсчет сигнала независим от предыдущего и может принимать любые значения. Для телеграфного текста это означает, что вероятность появления любой буквы алфавита одинакова и не зависит от того, какие буквы были переданы ранее. Но при передаче осмысленного текста все совсем не так! Вы смотрите на ленту телеграфного аппарата и читаете: «Добрый ден…». Стоп! Какая буква следующая?

Со стопроцентной уверенностью вы скажете, что «ь», и будете совершенно правы. Так сколько бит информации нес этот последний символ «ь»? А нисколько. Но на его передачу было затрачено пять двоичных разрядов. Таким образом, мы оценили максимально возможную скорость передачи информации. Она реализуется лишь для хаотических, случайных сигналов и беспорядочного набора символов, т. е. для нестандартных текстов.

В реальном тексте можно допустить довольно много пропусков и ошибок, почти не уменьшив количество переданной информации.

Возьмите текст стандартной телеграммы: «Поздр-м-с-ем ро-д-ния ж-ла с-a-тья зд-р-в-я ус-хо-». Из пятидесяти букв пропущено восемнадцать, более трети, и что же? Текст прекрасно восстанавливается. Несколько труднее было бы восстановить текст: «Грузите апельсины бочками», но и это нетрудно, если знать классиков юмористической литературы. А вот текст нестандартной поздравительной телеграммы: «Завидуем только сорок желаем новой весны». Здесь уже труднее выбросить часть букв, и не зря в таких случаях работники телеграфа делают к телеграммах приписку: «Текст верен».

Таким образом, действительное количество информации в сообщении является случайной величиной. Как и для любой случайной величины, можно найти среднее количество информации на символ (букву).

Первую попытку уменьшить количество передаваемой информации, повысив эффективность кодирования, предпринял еще С. Морзе, изобретатель телеграфной азбуки. Вместе с помощниками он изучил немало английской классической литературы, не вникая в смысл прочитанного, а подсчитывая количество различных букв в тексте. В результате была найдена относительная вероятность появления той или иной буквы. Чаще других встречалась буква «с», и ей была присвоена самая короткая кодовая комбинация — одна точка (·). Следующей по частоте появления оказалась «t», и эту букву обозначили одним тире (?). Ну а реже всех появлялись «j» (·???), «у» (?·??) и «q» (??·?), разумеется, они были обозначены самыми длинными кодовыми комбинатами. Код Морзе неравномерный, он неудобен для автоматического буквопечатающего телеграфа-телетайпа. В автоматических аппаратах используют равномерный код Бодо, в котором каждому символу — букве отводится пять двоичных знаков — посылок тока. Для автоматического телеграфа особую важность приобретают вопросы оптимального кодирования, которыми, в частности, и занимается наука, о которой я немного расскажу в следующем параграфе.