Энергия с горных вершин

Энергия с горных вершин

Недавно изобретенный Дедалом тепловой планер (см. «Тепловой планер») — летательный аппарат, использующий разность температур между верхними и нижними слоями атмосферы, — нетрудно преобразовать в более крупномасштабный проект. Значительная доля электрической энергии в современном обществе расходуется на кондиционирование воздуха. Поэтому большую ценность представляли бы способы непосредственного использования холода из верхних слоев атмосферы. Можно было бы, например, создать аэростат, поднимающийся вверх за счет подъемной силы газообразного аммиака и опускающийся на землю с грузом жидкого аммиака при -33°C. Более практичной, однако, была бы непрерывно действующая система. Поскольку температура воздуха падает с высотой на 6,5 градусов на километр, аэростат с теплообменником, поднятый на высоту 1–2 км и соединенный трубопроводами с поверхностью Земли, мог бы снабжать холодом дом или даже небольшой поселок[37]. Некоторые сложности возникнут только из-за ветра (потребуются дополнительные удерживающие растяжки); вряд ли удастся также создать такой аэростат действительно больших размеров.

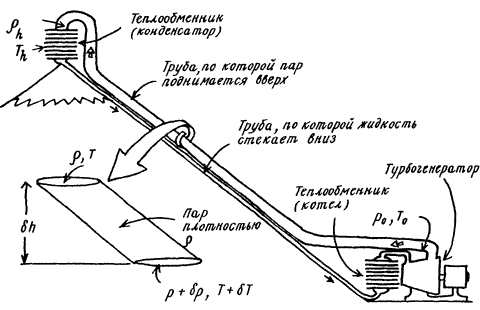
Поэтому для широкомасштабного использования существующих в атмосфере температурных градиентов Дедал разрабатывает план извлечения энергии с заснеженных горных вершин. Многообещающей в этом отношении является гора Кения — пятитысячник в экваториальной Африке; температура на ее вершине опускается до -18°C. Здесь можно было бы установить большой теплообменник и по склону горы проложить к нему трубы. По одной трубе газ поступает в теплообменник, где сжижается при низкой температуре; образовавшаяся жидкость стекает по второй трубе к подножию горы, где установлен второй теплообменник. Здесь газ, испаряясь, вращает турбогенератор; часть газа идет также в систему центрального охлаждения. Отработанный газ идет опять наверх и сжижается. Такая установка может снабжать холодом и энергией целый тропический город. У верхнего же теплообменника смогут обогреться дерзкие покорители горной вершины.

Подобрать подходящее рабочее тело такой системы непросто; прежде всего оно должно иметь низкую молекулярную массу, иначе давление высокого столба газа приведет к ее конденсации в нижней части. Подходящим кажется аммиак (М = 17), однако для того, чтобы он конденсировался при -18°C, давление должно составлять 2,2 атм — в таком случае понадобятся толстостенные и тяжелые трубы. Больше всего подходит метиламин. На вершине Кении он сконденсируется при 0,6 атм, что очень близко к атмосферному давлению на этой высоте. Кроме того, молекулярная масса метиламина близка к эффективной молекулярной массе воздуха (31 и 29 соответственно), так что изменение плотности метиламина с высотой точно следует изменению плотности атмосферы. Поэтому можно использовать легкие трубы. Экономически выгодными могут оказаться и менее крупномасштабные проекты — например, с вершины горы Бен-Невис снабжать энергией Форт-Уильям.

New Scientist, February 17, 1972

Из записной книжки Дедала

Чтобы изображенная на рисунке установка работала, конденсация должна происходить на вершине при р_hТ_h, а кипение у подножия — при р₀Т₀. Температуры на вершине и у подножия определяются атмосферными условиями, и мы не можем их изменить, тогда как величины давления зависят от рабочего тела и конструкции установки. Чем тяжелее газ, тем выше давление у подножия, тем выше точка кипения — и тем хуже обстоят наши дела. В предельном случае пары едва конденсируются наверху и жидкость еле-еле закипает внизу. Тогда в любой точке столба давление пара равно давлению насыщающих паров жидкости при данной температуре. Какую молекулярную массу должно иметь вещество, чтобы это условие выполнялось? В приближении идеального газа плотность пара равна ? = pm/RT, где р — давление, а m — молярная масса. Рассмотрим короткий участок трубы с перепадом высот ?h, заполненный паром. Если давление в верхнем сеченин равно р, то давление в нижнем сечении равно р = ?p, где ?р определяется из формулы гидростатического давления ?p = ?g?h = (pm/RT)g?h.

Итак, в предельном случае давление, создаваемое парами на любой высоте, равно давлению насыщающих паров (ДНП) жидкости на данной высоте. Поэтому, если в верхнем сечении ДНП жидкости при температуре Т равно р, то в нижнем сеченин, где температура равна Т+?Т, ДНП должно быть равно р+?р. Изменение ДНП жидкости с температурой хорошо описывается уравнением Клапейрона — Клаузиуса: ?р = ?р?Т/(РТ²), где ? — скрытая теплота испарения. Приравнивая между собой два выражения для ?р, получим ?p?T/(RT²) = (pm/RT)g?h, откуда m = (?Т/?р) ? (Tg) кг/моль.

Большинство жидкостей подчиняется эмпирическому правилу Трутона, согласно которому ?/Т равно приближенно 92 Дж/(моль•К), где Т — температура кипения (как всюду в нашей равновесной среде). Подставляя сюда температурный градиент стандартной модели атмосферы ?T/?h = 6,5?10^-3 К/м и g = 9,81 м/с², получим m = 6,5 ? 10^-3 ? 92/9,81 = 0,061 кг/моль = 61 г/моль.

Таким образом, нам может подойти только жидкость с молекулярной массой меньше 61, если только какие-то факторы, не учтенные в этих вычислениях, не будут играть нам на руку.

Попробуем проверить наши выводы для некоторых рабочих тел. Во-первых, «масштаб высоты» (соответствующий изменению давления в е раз) для идеального газа, если считать температуру постоянной, определяется соотношением Н = RT/gm. Тогда:

а. Аммиак (М=17, m = 0,017, Н = 13 600 м). На вершине горы Кения при -18°C аммиак конденсируется при давлении 2,2 атм; тогда у подножия горы, т. е. на 5000 м ниже, его давление р = 2,2 ехр(5000/13 600) = 3,2 атм. При таком давлении аммиак кипит при температуре -7°C. Следовательно, стекающий вниз жидкий аммиак будет кипеть в условиях тропической жары. Но, к сожалению, для этого требуется слишком высокое давление.

б. Метиламин (M = 31, m = 0,031 и Н = 7500 м). На вершине горы Кения при -18°C метиламин конденсируется при давлении 0,6 атм, а у подножия горы, т. е. на 5000 м ниже, давление в трубе составит р = 0,6 ехр(5000/7500) = 1,2 атм; при этом давлении метиламин кипит при температуре -5°C. Далее, поскольку давление воздуха на вершине горы равно 0,54 атм, а у подножия — 1 атм, давление внутри трубы на всем ее протяжении будет близко к наружному; поэтому трубопровод получится достаточно изящным и легким. По-видимому, метиламин вполне подходит для нашей цели.