3.6. Стегосистемы с бесконечными алфавитами

3.6. Стегосистемы с бесконечными алфавитами

Результаты, приведенные выше, могут быть расширены на случай стегосистем с бесконечными алфавитами контейнеров и стего X и ключей K. Заметим, что стегосистемы с непрерывными сообщениями и ключами существенно отличаются от известных криптографических систем. Для бесконечномерных сигналов существуют криптосистемы, например, использующие частотные или временные преобразования речи или изображений. Системы шифрования, в которых криптографические преобразования осуществляются над непрерывными в пространстве или времени сигналами, называются маскираторами и, как правило, не обеспечивают высокой криптографической стойкости [27]. Забегая вперед, скажем, что в отличие от криптосистем, для стегосистем с бесконечными алфавитами известны доказуемые оценки их устойчивости к атакам нарушителя. К тому же маскираторы используют ключ конечной длины, элементы которого принадлежат дискретному алфавиту. И, вообще, представить себе произвольную криптосистему с ключом, элементы которого принадлежат бесконечному алфавиту, довольно затруднительно.

Расширим определение взаимной информации для переменных 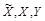и K стегосистемы, принадлежащих бесконечным алфавитам в виде [25]:

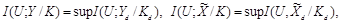
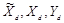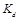где дискретные переменные и , принадлежащие конечным алфавитам, аппроксимируют с некоторой допустимой погрешностью соответствующие непрерывные переменные. Если все функции плотности вероятности являются абсолютно непрерывными, то результаты из пункта 3.3 справедливы при замене соответствующих сумм интегралами.

Особый интерес имеет случай контейнеров , распределенных по нормальному закону и оцениваемых среднеквадратической погрешностью вида 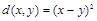. Назовем этот случай гауссовским контейнером. Он позволяет точно оценит величину скрытой ПС. Пусть множество X совпадает с множеством действительных значений, математическое ожидание значений отсчетов контейнера равно нулю и их дисперсия равна 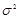. В дальнейшем будем использовать условное обозначение нормального распределения с математическим ожиданием 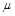и дисперсией 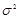в виде .

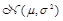Рассмотрим два случая. В первом случае секретным ключом К стегосистемы является контейнер . Во втором случае контейнер получателю не известен (слепая система скрытия информации).

Случай негауссовского распределения контейнера намного сложнее, но полезные результаты также могут быть получены. В частности, нижняя граница скрытой ПС может быть получена оценкой оптимальной атаки при конкретной, в общем случае подоптимальной, информационно-скрывающей стратегии 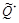. Нижние 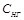и верхние 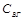границы скрытой ПС могут быть вычислены оценкой оптимальной информационно-скрывающей стратегии при конкретной, в общем случае подоптимальной, атаке :

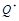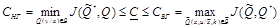. (3.18)

Эти границы полезны для негауссовских контейнеров, полагая что распределения 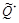и 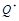выбраны соответствующим образом (см. пункт 3.8). Разумеется, если нижняя 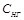и верхняя 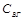границы в выражении (3.18) равны, пара распределений 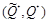дает седловую точку платежа в формуле (3.8).

Данный текст является ознакомительным фрагментом.