41. Уравнение состояния Ван-дер-Ваальса

41. Уравнение состояния Ван-дер-Ваальса

В общем случае для реальных газов при вычислении параметров состояния нельзя использовать уравнение состояния pv = RT,

которое верно для идеальных газов.

Общее уравнение состояния для реальных газов.

в котором коэффициенты B_i – называются вириальными. Эти коэффициенты являются функцией температуры молекул реального газа и потенциальной энергии их взаимодействия.

В определении В_i – коэффициентов производят расчет только первых двух членов ряда, остальные вириальные коэффициенты отбрасываются.

Тогда уравнение состояния для реальных газов принимает следующий вид:

где А и В – два первых вириальных коэффициента, зависящих только от температуры.

В частном случае (малая плотность газа) уравнение имеет форму:

Если В₁ = f(T, U_потенц), то уравнение превращается в уравнение состояния для реального газа Ван-дер-Ваальса:

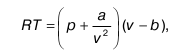
где b– минимальный объем, который может приобретать реальный газ при сжатии;

а – коэффициент, не являющийся функцией параметров состояния.

Для разных газов величины а и b различны.

Иными словами, уравнение Ван-дер-Ваальса – это частный случай закона Боголюбова-Майера, в котором пренебрегают всеми членами 1/v выше второй степени. Если реальный газ имеет высокую плотность, то уравнения такого типа будут верны при большем количестве членов ряда. В этом случае уравнения состояния реальных газов дают точность вычислений, приемлемую на практике.