48. Уравнение неразрывности

48. Уравнение неразрывности

Согласно газовой теории потока течение газа в случае стационарности определяется с помощью специальной системы уравнений. В нее входят следующие соотношения:

1) уравнение энергии для газового потока;

2) уравнение состояния;

3) уравнение для неразрывности газового потока.

Уравнение энергии следует из первого начала

термодинамики для газовых потоков.

Уравнением неразрывности называется соотношение:

Gv = Fw.

Из него следует, что в случае установившегося течения газа в каждом сечении потока расход газа по массе является постоянной величиной. Иначе это уравнение можно записать в виде:

G =pFw =p₁F₁w₁ =P₂F₂w₂ =const,

где r₁,r₂, r= 1/v плотность газа в поперечных сечениях;

F₁, F₂– площадь сечения потока;

w₁, w₂– скорость потока, измеряется в области сечения.

В данном случае имеется два сечения потока (1-е и 2-е), а величина Gиз этого уравнения называется массовым расходом газа (в секунду).

Как известно, второй закон Ньютона гласит: «Сила определяется произведением массы и ускорения». Если газовый поток имеет одномерный характер, то из второго закона следует:

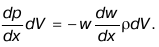
В данном соотношении каждый член имеет определенное физическое значение. Рассмотрим каждый множитель из уравнения.

1. Величина

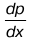
показывает, как изменяется давление в зависимости от Х-координаты.

2. Величина

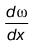
показывает, как изменяется скорость в зависимости от Х-координаты.

3. Соотношение

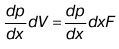
равно силе, приложенной к элементарному объему, dV – выделенный объем.

dw

4. Величина

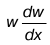
газа равна ускорению массы pdV(элементарная масса).