33. Уравнение Бернулли для движения вязкой жидкости
33. Уравнение Бернулли для движения вязкой жидкости
Элементарная струйка при установившемся движении вязкой жидкости
Уравнение для этого случая имеет вид (приводим его без вывода, поскольку его вывод сопряжен с применением некоторых операций, приведение которых усложнило бы текст)
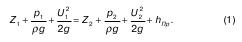
Потеря напора (или удельной энергии) hПp – результат того, что часть энергии превращается из механической в тепловую. Поскольку процесс необратим, то имеет место потеря напора.
Этот процесс называется диссипацией энергии.
Другими словами, hПp можно рассматривать как разность между удельной энергией двух сечений, при движении жидкости от одного к другому происходит потеря напора. Удельная энергия – это энергия, которую содержит единичная масса.
Поток с установившимся плавно изменяющемся движением. Коэффициент удельной кинематической энергии Х
Для того, чтобы получить уравнение Бернулли в этом случае, приходится исходить из уравнения (1), то есть из струйки надо переходить в поток. Но для этого нужно определиться, что представляет собой энергия потока (которая состоит из суммы потенциальной и кинематической энергий) при плавно изменяющемся потоке
Разберемся с потенциальной энергией: при плавном изменении движения, если поток установившийся
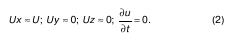
Окончательно при рассматриваемом движении давление по живому сечению распределено согласно гидростатическому закону, т. е.

где величину Х называют коэффициентом кинетической энергии, или коэффициентом Кориолиса.
Коэффициент Х всегда больше 1. Из (4) следует:

Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.
Читайте также
Административный регламент Министерства внутренних дел Российской Федерации исполнения государственной функции по контролю и надзору за соблюдением участниками дорожного движения требований в области обеспечения безопасности дорожного движения
Административный регламент Министерства внутренних дел Российской Федерации исполнения государственной функции по контролю и надзору за соблюдением участниками дорожного движения требований в области обеспечения безопасности дорожного движения Приложение к
14. Методы определения движения жидкости
14. Методы определения движения жидкости Гидростатика изучает жидкость в ее равновесном состоянии.Кинематика жидкости изучает жидкость в движении, не рассматривая сил, порождавших или сопровождавших это движение.Гидродинамика также изучает движение жидкости, но в
19. Уравнение неразрывности жидкости
19. Уравнение неразрывности жидкости Довольно часто при решении задач приходится определять неизвестные функции типа:1) р = р (х, у, z, t) – давление;2) nx(х, у, z, t), ny(х, у, z, t), nz(х, у, z, t) – проекции скорости на оси координат х, у, z;3) ? (х, у, z, t) – плотность жидкости.Эти неизвестные,
22. Дифференциальные уравнения движения невязкой жидкости
22. Дифференциальные уравнения движения невязкой жидкости Уравнение Эйлера служит одним из фундаментальных в гидравлике, наряду с уравнением Бернулли и некоторыми другими.Изучение гидравлики как таковой практически начинается с уравнения Эйлера, которое служит
24. Форма Громеки уравнения движения невязкой жидкости
24. Форма Громеки уравнения движения невязкой жидкости Уравнения Громеки – попросту другая, несколько преобразованная форма записи уравнения Эйлера.Например, для координаты x Чтобы его преобразовать, используют уравнения компонентов угловой скорости для вихревого
25. Уравнение Бернулли
25. Уравнение Бернулли Уравнение Громеки подходит для описания движения жидкости, если компоненты функции движения содержат какуююто вихревую величину. Например, эта вихревая величина содержится в компонентах ?x, ?y,?z угловой скорости w.Условием того, что движение
26. Анализ уравнения Бернулли
26. Анализ уравнения Бернулли это уравнение есть не что иное, как уравнение линии тока при установившемся движении.Отсюда следуют выводы:1) если движение установившееся, то первая и третья строки в уравнении Бернулли пропорциональны.2) пропорциональны строки 1 и 2,
27. Примеры прикладного применения уравнения Бернулли
27. Примеры прикладного применения уравнения Бернулли Во всех случаях требуется определить математическую формулу потенциальной функции, которая входит в уравнение Бернулли: но эта функция имеет разные формулы в разных ситуациях. Ее вид зависит от того, какие массовые
29. Энергетический смысл уравнения Бернулли
29. Энергетический смысл уравнения Бернулли Пусть теперь имеем установившееся движение жидкости, которая невязкая, несжимаемая.И пусть она находится под воздействием сил тяжести и давления, тогда уравнение Бернулли имеет вид: Теперь требуется идентифицировать каждое
30. Геометрический смысл уравнения Бернулли
30. Геометрический смысл уравнения Бернулли Основу теоретической части такой интерпретации составляет гидравлическое понятие напор, которое принято обозначать буквой Н, где Гидродинамический напор Н состоит из следующих разновидностей напоров, которые входят в
31. Уравнения движения вязкой жидкости
31. Уравнения движения вязкой жидкости Для получения уравнения движения вязкой жидкости рассмотрим такой же объем жидкости dV = dxdydz, который принадлежит вязкой жидкости (рис. 1).Грани этого объема обозначим как 1, 2, 3, 4, 5, 6. Рис. 1. Силы, действующие на элементарный объем
32. Деформация в движущейся вязкой жидкости
32. Деформация в движущейся вязкой жидкости В вязкой жидкости имеются силы трения, в силу этого при движении один слой тормозит другой. В итоге возникает сжатие, деформация жидкости. Из-за этого свойства жидкость и называют вязкой.Если вспомнить из механики закон Гука, то
35. Уравнение Бернулли для неустановившегося движения вязкой жидкости
35. Уравнение Бернулли для неустановившегося движения вязкой жидкости Для того, чтобы получить уравнение Бернулли, придется определить его для элементарной струйки при неустановившемся движении вязкой жидкости, а затем распространять его на весь потокПрежде всего,
36. Ламинарный и турбулентный режимы движения жидкости. Число Рейнольдса
36. Ламинарный и турбулентный режимы движения жидкости. Число Рейнольдса Как нетрудно было убедиться в вышеприведенном опыте, если фиксировать две скорости в прямом и обратном переходах движения в режимы ламинарное ? турбулентное, то?1 ? ?2где ?1 – скорость, при которой
41. Уравнение состояния Ван-дер-Ваальса
41. Уравнение состояния Ван-дер-Ваальса В общем случае для реальных газов при вычислении параметров состояния нельзя использовать уравнение состояния pv = RT,которое верно для идеальных газов.Общее уравнение состояния для реальных газов. в котором коэффициенты Bi –
48. Уравнение неразрывности
48. Уравнение неразрывности Согласно газовой теории потока течение газа в случае стационарности определяется с помощью специальной системы уравнений. В нее входят следующие соотношения:1) уравнение энергии для газового потока;2) уравнение состояния;3) уравнение для