Глава 3. Индуктивность… Добротность… Резонанс…
«Аматор»: Заходи-заходи, дружище!
«Незнайкин»: У тебя, как ты мне признался по телефону, есть время, а у меня и время, и желание продолжить разговор на тему электромагнитной индукции!
«А»: «Я очень счастлив и рад за вас!». Полагаю, что продолжить разговор об электромагнитной индукции просто необходимо, поскольку с ее характером следует познакомиться поближе. А характер у нее весьма упрямый!
«Н»: В каком смысле — «упрямый»?
«А»: Да в самом, что ни на есть, прямом! Дело в том, что наведенный во вторичной обмотке, иначе говоря, ИНДУЦИРОВАННЫЙ ТОК I2 ВСЕГДА находится в противофазе с индуцирующим током I,! Если индуцирующий ток увеличивается в одном направлении, то индуцированный ток — течет в противоположном направлении, как бы препятствуя увеличению первого! А когда индуцирующий ток уменьшается, индуцированный ток течет В ТОМ ЖЕ НАПРАВЛЕНИИ, как бы препятствуя уменьшению первого! Взгляни на рис. 2.8.
«Н»: И ты считаешь, что эту головоломку я запомню и пойму?
«А»: Выше голову! Ведь сказанное ранее можно сформулировать и более кратко. Например, так:
ИНДУЦИРОВАННЫЙ ТОК ВСЕГДА ИМЕЕТ ТАКОЕ НАПРАВЛЕНИЕ, КОТОРОЕ ПРОТИВОДЕЙСТВУЕТ ЛЮБЫМ ИЗМЕНЕНИЯМ ИНДУЦИРУЮЩЕГО ТОКА!
Я скажу даже больше, чем БЫСТРЕЕ происходит изменение величины тока в первичной обмотке, тем сильнее реакция вторичной обмотки!
«Н»: То есть ВЕЛИЧИНА ИНДУЦИРОВАННОГО ТОКА ПРОПОРЦИОНАЛЬНА СКОРОСТИ ИЗМЕНЕНИЯ ИНДУЦИРУЮЩЕГО ТОКА, а также его ВЕЛИЧИНЕ?
«А»: Правильно совершенно!
«Н»: Вот тебе и «простой медный провод»! Удивительный эффект!
«А»: Но и это еще не все!.. Как ты думаешь, что произойдет в такой вот простенькой схемке (рис. 3.1)?
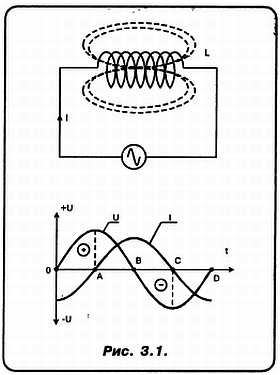
«Н»: Сейчас-сейчас, только график набросаю… Готово! Теперь будем рассуждать, как на эпюру напряжения на индуктивности L наложится эпюра тока.
«А»: В момент А изменение напряжения во времени (т. е. ΔU/Δt) минимально. Поэтому ток равен НУЛЮ! Затем напряжение на участке АВ падает до НУЛЯ. Но при этом отношение ΔU/Δt — ВОЗРАСТАЕТ! Поэтому генерируемый электромагнитным полем индуктивности L ток I имеет такое направление, чтобы не дать напряжению на выводах индуктивности L упасть до нуля! То есть в этом случае в точке В ток максимален, а его полярность положительна!
Но вот напряжение генератора становится отрицательным. И отношение ΔU/Δt — уменьшается! Ток I по-прежнему положителен, но его величина падает, становясь равной нулю в точке С. В тоже время в этой точке амплитуда отрицательной полуволны напряжения максимальна! Но когда на участке CD амплитуда напряжения падает, генерируемый электромагнитным полем индуктивности ток I возрастает, но теперь этот ток имеет отрицательную полярность, поскольку он препятствует спаданию напряжения на индуктивности до нуля!
«Н»: Если я правильно понял, электромагнитная индукция может индуцировать ток даже в своих собственных витках?
«А»: Ну конечно. В этом случае это явление именуется как САМОИНДУКЦИЯ!
«Н»: Я вспоминаю твой рассказ о временах Пунических войн! Помнишь, ты рассказывал о римском сенаторе, который свои выступления в сенате на тему о проблемах римского плебса, на тему об улучшении торговли, благоустройстве дорог и так далее, заканчивал всегда одной и той же фразой!..
«А»: «Карфаген должен быть разрушен!»? То есть ты снова намекаешь на то, какое отношение все наши рассуждения об удивительных свойствах индуктивностей и емкостей имеют к электронике?
«Н»: Ты прав, о высокочтительный друг мой!
«А»: А вот ты, Незнайкин, не совсем! Только теперь мы подошли к самому интересному. Как ты думаешь… А впрочем, я виноват в том что мы еще ничего не сказали о том, что является основной единицей индуктивности. Так вот, в качестве таковой принят ОДИН ГЕНРИ.
1 ГЕНРИ — это такая индуктивность, при которой изменение напряжение на ее выводах на 1 вольт в течении 1 секунды вызывает появление противодействующего такому изменению тока, равного 1 амперу. Заметим, что вообще 1 генри — это исключительно большая индуктивность, которая нигде не встречается. Поэтому в ходу более мелкие единицы:
1 генри = 1000 миллигенри = 1000000 микрогенри.
А теперь — последнее, Незнайкин! Как мы ранее уже могли убедиться, поскольку при приложении напряжения к индуктивности (из-за присущей ей инерции) происходит отставание тока от напряжения, то говорят, что ток отстает по фазе. Любопытно, что для емкости, ток опережает по фазе напряжение! А теперь — вопросы.
«Н»: Ты как-то употребил в разговоре выражение — реактивное сопротивление! Что же это такое и присуще ли оно только емкости?
«А»: Нет, не только! Индуктивность тоже характеризуется реактивным сопротивлением. В самом общем смысле этот термин означает, что реактивная мощность, равная произведению мгновенного значения емкостного (или индуктивного) тока на напряжение не преобразуется в тепло! Поскольку она затрачивается не на увеличение амплитуды тепловых колебаний атомов кристаллической решетки, как в случае активного сопротивления, а на изменение интенсивности электромагнитного поля (в индуктивности) или на поляризацию диполей изолятора (в конденсаторе). А это, практически, не носит теплового характера…
«Н»: Все это дьявольски интересно!
«А»: Еще бы!.. Но в мире слишком много интересного, поверь! А потому не хочешь ли немного пожонглировать?
«Н»: Соскучился по цирку? Что предпочитаешь?… Шары, мячи… Может тарелки?…
«А»: Расслабься! Посуда останется целой, ручаюсь… И жонглировать мы будем не тарелками или шарами, а… резисторами, конденсаторами и индуктивностями! Причем на бумаге!..
«Н»: Как это… как это… как это?..
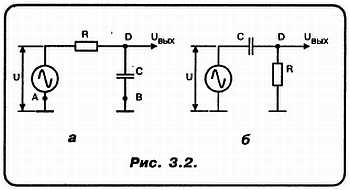
«А»: Очень просто. Мы «разрисуем» целый ряд «простеньких» схемок, состоящих из различных комбинаций R, L и С. После чего ознакомимся с их свойствами… Итак, начнем вот с чего (см. рис. 3.2)… По глазам твоим вижу, Незнайкин, что ты хочешь меня о чем-то спросить!
«Н»: А то нет?! Ты мне столько рассказывал, что электрические цепи должны быть замкнуты… А что нарисовал?
«А»: Тебя смущает, что точки А и В не соединены между собой? Не сомневайся — превосходно соединены! Эти вот значки, напоминающие «перекладины», «гребешки» и «щеточки», символизируют, ласкающий слух радистов, термин — ЗАЗЕМЛЕНИЕ или КОРПУС!
Реально эти точки всегда располагаются на обшей металлической шине или массивном проводнике. Поэтому, чтобы не загромождать принципиальные электрические схемы, условились общий проводник (провод) или корпус не изображать, а пользоваться особыми условными обозначениями. Один из вариантов таких обозначений ты и наблюдаешь!
А теперь, маэстро, ваш выход! Прошу зарисовать АЧХ как для схемы рис. 3.2, а, так и для схемы рис. 3.2, б.
«Н»: «Извольте, я готов…, но я в большой надежде, что термин АЧХ… мне разъясните прежде?»
«А»: Вот ты уже, Незнайкин, стихами заговорил!.. АЧХ — это аббревиатура, которая расшифровывается как АМПЛИТУДНО-ЧАСТОТНАЯ ХАРАКТЕРИСТИКА! Ее смысл — наглядно показать, как изменяется напряжение в какой-либо точке в зависимости от частоты генератора переменного напряжения.
«Н»: Так частота генератора переменного напряжения НЕПОСТОЯННАЯ величина?
«А»: Ну конечно!.. А то чего ради мы потратили столько времени и усилий, вникая в суть индуктивностей и емкостей?
«Н»: Будет лучше, если ты изобразишь это графически!
«А»: Ладно!.. Я рисую график! Ординате присваиваю обозначение А, тогда абсциссе — f. По английски f — friquensi — (частота) (см. рис. 3.3)! Тогда А, соответственно, амплитуда.
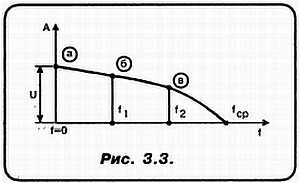
Пусть амплитуда переменного напряжения, генерируемого источником, постоянна и равна U для любой из генерируемых частот. При f = 0, то есть в нашем случае U просто некоторое постоянное напряжение. Соответственно, в точке D (рис. 3.2, а) установится напряжение, равное U. Эта точка на графике обозначена, как «а».
Повысим частоту генератора до f1. Естественно, что это приведет к заряду (или разряду в зависимости от полупериода) конденсатора С. Но в этом случае зарядно-разрядный ток, проходя по резистору R, создает на нем соответствующее падение напряжения. Поэтому теперь напряжение в точке D будет меньше, чем U. На графике это соответствует точке «б».
Увеличим частоту генератора и приравняем ее f2. Напряжение на выходе стало еще меньше. Это и отображает точка «в». Так будет продолжаться до тех пор. пока частота не станет равной частоте среза fср. На этой частоте уже ВСЕ напряжение источника падает на активном сопротивлении!
«Н»: Выходит, что дальнейшее увеличение частоты генератора уже бессмысленно?
«А»: В точности так! А теперь, Незнайкин, раздраконь мне так же схемку на рис. 3.2,б.
«Н»: С нашим удовольствием… Вот график (рис. 3.4)! Все верно?
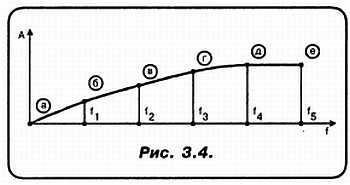
«А»: Мне остается только (и с полным на то правом) повторить слова «великого кормчего» Мао-цзе-дуна к его приемнику Хуа-го-фену: «Если дело в твоих руках, я спокоен!» Тем более, что ты предъявил реальный график, а не утопию!
«Н»: Но ты обратил внимание, что в точках графика «д» и «е» амплитуда одна и та же?
«А»: Поверь, я от всей души рад, что ты это подметил! А что ты скажешь по поводу вот этих двух схемок (рис. 3.5)?
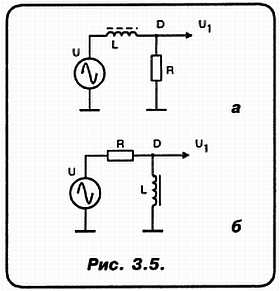
«Н»: Вот, прошу. И для случая а и для случая б. Возражения есть (рис. 3.6)?
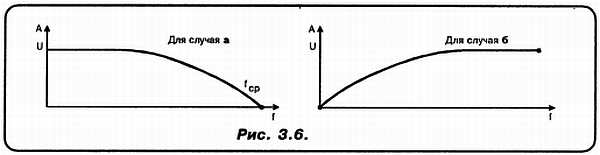
«А»: Пока — никаких! Но я проявлю известную толерантность и не стану вот так, с места в карьер требовать, чтобы ты нарисовал мне АЧХ вот такой «скромной» схемки (рис. 3.7).
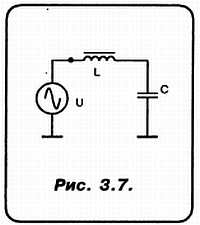
«Н»: Да что в ней особенного-то! Сейчас-сейчас. Нет, знаешь, что-то не выходит!..
«А»: Остынь, дружище! И, чтобы не тратить время напрасно, послушай, что в действительности представляет из себя вышепредложенная схема! Ты уже знаешь, что с возрастанием частоты индуктивное сопротивление (XL) увеличивается, а емкостное сопротивление (ХС) — уменьшается! Но отсюда следует, что при некоторой частоте f0 — индуктивное и емкостное сопротивления становятся равными. И в этот момент общее реактивное сопротивление цепи СТРЕМИТСЯ К НУЛЮ! Вспомним о сдвигах по фазе!
Так вот, когда частота генератора равна никакого сдвига по фазе между напряжением и током — НЕ БУДЕТ! Эта ситуация получила название — РЕЗОНАНС!
«Н»: Я знал, что есть механический резонанс…
«А»: Ну, примеры потрясающих случаев механического резонанса можно найти даже в Библии. Например, Иерихонские трубы!
«Н»: Действительно…
«А»: Итак, мы видим, что электрическая цепь, состоящая из емкости С и индуктивности L, обладает собственной резонансной частотой f0! При этом общее сопротивление цепи становится очень малым, а амплитуда колебаний тока в ней — очень большой!
«Н»: Но почему ты говоришь «очень малым», а не говоришь — «нулевым»?
«А»: Ты прав, мой милый граф! Это только из-за того, что индуктивность L — это ведь изолированный провод, намотанный на сердечник. А провод, как известно, имеет еще и активное сопротивление, хотя и очень небольшое. Поэтому, в реальном случае, предыдущая схема выглядит так (рис. 3.8).
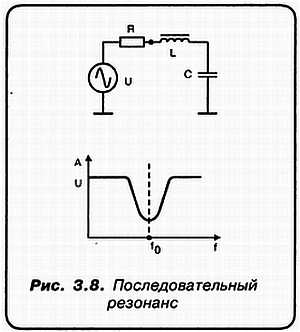
«Н»: А я готов нарисовать АЧХ этой схемы! Смотри, я даже учел тот факт, что из-за наличия активного сопротивления R «провал» АЧХ не имеет общей точки с осью абсцисс!
«А»: Я начинаю думать, что если дело и дальше пойдет так же успешно, то не только я, но и Спец запишется на цикл твоих лекций по электронике! Ну, а теперь я прошу тебя подумать, что будет в таком случае (рис. 3.9)…
Да, учти следующее обстоятельство. То, о чем мы сейчас говорим, я имею в виду электрический резонанс, — это «святая святых» радиотехники вообще и техники радиоприема, в частности!
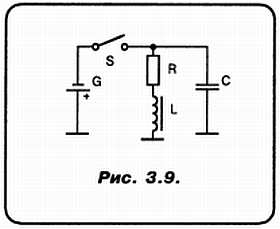
«Н»: Что я вижу!? Ты заменил генератор переменного тока на батарейку? К чему бы это?
«А»: Мы подключили батарейку к нашей схеме посредством выключателя, а затем отключили ее! Вот с этого момента мы и начнем анализ…
«Н»: А что же тут анализировать? Конденсатор просто разрядится через резистор R и индуктивность L! И все дела!..
«А»: Да, кроме шуток?
«Н»: Нет-нет, прости! Не совсем… Что-то еще здесь произойдет… Но я пока не врубился — что!..
«А»: Вспомни, Незнайкин, что индуктивность L обладает некоторой инерцией. Образно говоря, из-за нее электронам так же трудно начать упорядоченное движение, как и прекратить это движение!
Ток разряда, проходя по виткам индуктивности L, порождает магнитное поле, в котором запасается некоторая энергия! Таким образом, в тот момент, когда конденсатор С уже разрядится, магнитное поле будет поддерживать упорядоченное движение электронов в том же направлении! Это значит, что до того момента, как энергия магнитного поля иссякнет, конденсатор успеет перезарядиться почти до первоначального напряжения! Хотя и ПРОТИВОПОЛОЖНОЙ ПОЛЯРНОСТИ! Затем снова наступит цикл перезаряда. И так будет продолжаться до того момента, пока на активном сопротивлении R (а оно в неявном виде ВСЕГДА присутствует в рассматриваемой системе) постепенно не перейдет в тепло ВСЯ первоначально запасенная в конденсаторе энергия!
«Н»: А рассмотренная система, состоящая из L, С и R, не имеет имени собственного?
«А»: Обязательно! И отныне мы будем употреблять только его — КОЛЕБАТЕЛЬНЫЙ КОНТУР!
«Н»: А как долго будет продолжаться подобная циркуляция тока в контуре? От чего это зависит?
«А»: Есть такой удивительный параметр — ДОБРОТНОСТЬ! Вот он то и, определяет, как долго в контуре будут продолжаться колебания.
«Н»: А почему ты назвал этот параметр — «удивительным»?
«А»: Да хотя бы потому, что он как бы един в трех лицах!
«Н»: А это как?
«А»: Да вот, посмотри на рисунок! На рис. 3.10,а изображены незатухающие электромагнитные колебания, которые имели бы место в контуре без потерь. На рис. 3.10,б изображены реальные, ЗАТУХАЮЩИЕ колебания в контуре.
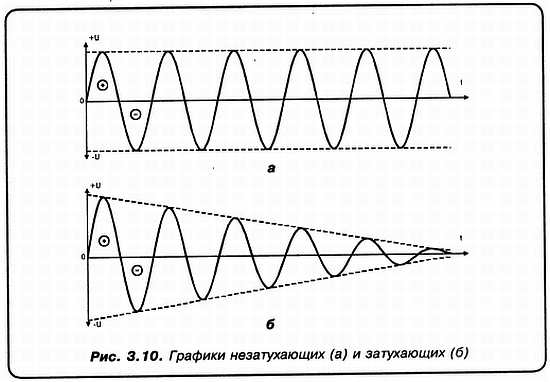
Так вот, численно, количество полных циклов заряд — разряд до, практически, полного затухания РАВНО ДОБРОТНОСТИ! Т. е. добротность Q = n, где n — количество полных циклов. А теперь от амплитудно-временных характеристик перейдем к АЧХ (рис. 3.11).
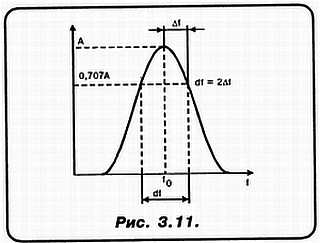
Вот эта, колоколообразная кривая (мы к ее рассмотрению вернемся в дальнейшем еще не раз) дает вторую, практически очень важную характеристику для Q:
Q = f0/2Δf,
где Δf — полоса пропускания по уровню 0,707.
И, кроме того, вот третья ипостась добротности, численно равная:
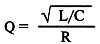
И если первая ипостась очень понятна, но не очень наглядна, поскольку кто успеет подсчитать точное число колебаний за очень малый промежуток времени, то вторая ипостась — может прямо выводиться на экран специальных анализаторов АЧХ! С ней удобно работать!
«Н»: Ну, а третья?
«А»: Третья ипостась — для реальных расчетов! Но любой колебательный контур характеризуется еще и частотой резонанса, или, что адекватно, частотой собственных колебаний:
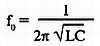
Любопытно, что для получения одной и той же f0, можно взять различное соотношение L и С. Но формула для определения добротности показывает, каким именно должно быть соотношение L и С для получения требующейся нам ПОЛОСЫ ПРОПУСКАНИЯ КОЛЕБАТЕЛЬНОГО КОНТУРА! Она обозначена как df = 2Δf
«Н»: А какого порядка эта величина должна быть?
«А»: Смотря для чего! А вообще получение высоких добротностей — это сложная техническая задача! Но, в общем, вполне решаемая! Сейчас нам осталось рассмотреть еще одну важную физическую, а равно и техническую особенность колебательных контуров!
«Н»: Ты снова рисуешь схему?
«А»: А куда деваться (см. рис. 3.12)?
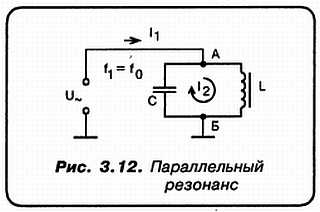
Здесь колебательный контур включен непосредственно в состав некоторой внешней цепи. Обрати внимание, Незнайкин, что в этом случае, когда частота внешнего генератора f1 совпадает с собственной частотой контура, последний представляет собой ЗНАЧИТЕЛЬНОЕ РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ для ВНЕШНЕЙ ЦЕПИ!
«Н»: Но при этом ВНУТРИ контура LC реактивное сопротивление МАЛО!?
«А»: Да, конечно!.. Дело в том, что за каждый период собственных колебаний контур LC теряет МАЛУЮ часть запасенной в нем энергии! Следовательно, этот контур будет потреблять из ВНЕШНЕЙ цепи ТОЛЬКО такую часть энергии, которая идет на компенсацию потерь за этот период! А это — очень незначительная величина! И она тем меньше, чем больше добротность контура Q!
«Н»: То есть, если я верно понял, на резонансной частоте по отношению ко ВНЕШНЕЙ ЦЕПИ контур является БОЛЬШИМ СОПРОТИВЛЕНИЕМ, причем тем большим, чем больше его добротность?
«А»: Абсолютно точно! Но есть и еще одно исключительно важное следствие! Не догадываешься, какое именно?
«Н»: Может быть (см. рис. 3.12) что мы можем написать:
I2 = I1Q
Так или нет?
«А»: Замечательно! Ну а что ты скажешь относительно напряжения?
«Н»: У меня создалось впечатление, что напряжение на зажимах А и Б контура… может превысить напряжение генератора!
«А»: И ты не ошибся! Оно превышает на частоте собственного резонанса подводимые извне колебания по амплитуде в Q раз!
«Н»: То есть колебательный контур УСИЛИВАЕТ частоту, равную его резонансной в Q раз?
«А»: Да! Но если во внешней цепи будут протекать токи, частоты которых не совпадают с резонансной, то они не создадут на зажимах контура сколько-нибудь заметного напряжения! Поэтому РЕЗОНАНСНЫЙ КОНТУР ОБЛАДАЕТ ЧАСТОТНОЙ ИЗБИРАТЕЛЬНОСТЬЮ!
«Н»: Я уже дошел до кондиции, как того и хотел герой «Бриллиантовой руки». Всю впитанную (с кровью) информацию я должен осмыслить. В общем «принять ванну и выпить чашечку кофе»…
«А»: Мы кое-что успели сегодня, дружище!
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК