Святой Грааль криптографии

Первая мировая война продемонстрировала ряд побед криптоаналитиков; венцом стало дешифрование телеграммы Циммермана. С момента взлома шифра Виженера в девятнадцатом веке криптоаналитики постоянно одерживали верх над криптографами.

Но к концу войны, когда криптографы пребывали в полном отчаянии, ученые в Америке сделали поразительное открытие. Они обнаружили, что шифр Виженера может быть использован в качестве основы для нового, гораздо более труднопреодолимого вида шифрования. На самом деле этот новый шифр мог обеспечить абсолютную стойкость.

Основная слабость шифра Виженера заключается в том, что ему присуща периодичность. Если длина ключевого слова составляла пять букв, то каждая пятая буква открытого текста шифровалась с использованием одного и того же шифралфавита. Если криптоаналитик мог определить длину ключевого слова, то с зашифрованным текстом можно было поступать как с набором пяти одноалфавитных шифров, и каждый из них мог быть дешифрован с помощью частотного анализа. Посмотрим, однако, что произойдет по мере увеличения длины ключевого слова.

Допустим, что у нас есть открытый текст, состоящий из 1 000 букв и зашифрованный с помощью шифра Виженера; проведем криптоанализ имеющегося шифртекста. Если длина ключевого слова, используемого для шифрования открытого текста составляет всего 5 букв, то на завершающем этапе криптоанализа потребуется провести частотный анализ 5 наборов из 200 букв, что не представляет труда. Но если ключевое слово состоит из 20 букв, то на завершающем этапе необходимо будет провести частотный анализ 20 наборов из 50 букв, что уже значительно сложнее. Если же ключевое слово состоит из 1000 букв, то вы столкнетесь с тем, что придется провести частотный анализ 1000 наборов, каждый из которых состоит из 1 буквы, что совершенно невыполнимо. Другими словами, если длина ключевого слова (или ключевой фразы) совпадает с длиной сообщения, то криптоаналитический метод, разработанный Бэббиджем и Касиски не работает.

Так что когда применяется ключ той же длины, что и сообщение, то все хорошо и прекрасно, правда, это требует от криптографа создания длинного ключа. Так что если сообщение состоит из сотен букв, то и длина ключа также должна составлять сотни букв. Однако чем придумывать длинный ключ, невольно напрашивается мысль использовать в качестве него, ну, скажем, лирическое стихотворение. Или же криптограф может приобрести книгу по ловле птиц и создать ключ на основе нескольких случайно выбранных названий птиц. Но такие упрощенные ключи по своей сути порочны.

В следующем примере я зашифровал отрывок текста с помощью шифра Виженера, используя ключевую фразу такой же длины, что и сообщение. Применение любых методов криптоанализа, о которых я писал раньше, окажется безуспешным. Но сообщение все же можно дешифровать.

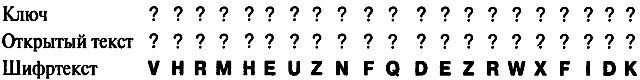
Этот новый способ криптоанализа начинается с предположения, что в шифртексте содержатся общеупотребительные слова, к примеру, the. Далее, как показано ниже, мы произвольным образом подставляем the в различные места в открытом тексте и определяем, какими должны быть буквы ключа, чтобы преобразовать the в соответствующий шифртекст. Итак, мы решили, что the будет являться первым словом открытого текста. Первая буква ключа будет зашифровывать t в V. Чтобы определить первую букву ключа, возьмем квадрат Виженера и будем двигаться сверху вниз по столбцу, начинающемуся с буквы t, пока не дойдем до V; буква, с которой начинается эта строка — С. Повторим этот процесс для h и e, которые были зашифрованы как H и R соответственно; в конечном счете мы получим возможные значения первых трех букв ключа — CAN. Все это получено в предположении, что слово the является первым словом открытого текста. Подставим the в несколько других мест и вновь поищем соответствующие буквы ключа. (Вы можете проверить соответствие между каждой буквой открытого текста и буквой шифртекста, обратившись к квадрату Виженера в таблице 9.)

Мы проверили три слова the в трех произвольно выбранных местах шифртекста и выдвинули три предположения относительно элементов определенных частей ключа. Можем ли мы сказать, что какое-нибудь из слов the стоит в нужном месте? Мы предполагаем, что ключ состоит из осмысленных слов; попробуем использовать это в наших целях. Если the стоит не на своем месте, то это приведет, скорее всего, к тому, что ключ будет состоять из хаотичного набора букв. Если же оно стоит в нужном месте, то буквы ключа должны иметь какой-то смысл. Например, первое the дает буквы ключа CAN, что обнадеживает, поскольку это вполне нормальный английский слог. Так что возможно, что это слово the стоит на своем месте. Второе the дает BSJ, — весьма странное сочетание согласных, что позволяет предположить, что второе the, скорее всего, неверно. Для третьего the получается YPT, — редко встречающийся слог, но ею все же стоит проверить. Если YPT действительно является частью ключа, то оно должно находиться внутри более длинного слова; такими словами могут быть только APOCALYPTIC, CRYPT и EGYPT и производные от этих слов. Как мы сможем определить, является ли одно из этих слов частью ключа?

Мы может проверить каждое предположение, подставляя все эти три слова в ключ над соответствующим куском шифртекста и находя соответствующий открытый текст:

Если слово не является частью ключа, то, скорее всего, это опять-таки приведет к тому, что фрагмент открытого текста будет состоять из хаотичного набора букв; если же оно является частью ключа, то получающийся открытый текст должен иметь определенный смысл. При использовании в качестве части ключа слова APOCALYPTIC, получающийся открытый текст состоит из абсолютно бессмысленного набора букв. При использовании в качестве части ключа слова CRYPT, в открытом тексте получается cithe, что, в общем-то, не является невозможным куском открытого текста. Однако если в качестве части ключа использовать EGYPT, то при этом получается atthe — более обещающая комбинация букв, которая, видимо, представляет собой слова at the.

Предположим пока, что скорее всего в качестве части ключа используется EGYPT. Возможно, что в качестве ключа используется перечень стран. А это означает, что CAN, часть ключа, которая соответствует первому the, является началом слова CANADA. Мы можем проверить эту гипотезу, предполагая, что CANADA, как и EGYPT, являются частями ключа, если откроем б?льший фрагмент открытого текста:

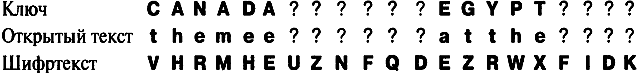
Похоже, что наше предположение имеет смысл. CANADA означает, что открытый текст начинается с themee, что, по-видимому, является началом the meeting. Теперь, когда мы определили новые буквы открытого текста, ting, мы можем найти соответствующую им часть ключа; это будет BRAZ, которое, несомненно, является началом слова BRAZIL. Используя в качестве ключа комбинацию CANADABRAZILEGYPT, мы получим следующее: the meeting is at the????.

Чтобы найти завершающее слово открытого текста — место встречи, — лучше всего завершить составление ключа путем проверки перебором названий всех возможных стран, оценивая получающийся при этом открытый текст. Осмысленный открытый текст получается только в случае, когда конечным элементом ключа будет слово CUBA:

_{Таблица 9 Квадрат Виженера.}

Поэтому для обеспечения стойкости недостаточно, чтобы ключ имел такую же длину, что и само сообщение. В приведенном выше примере уязвимость возникла из-за того, что ключ был создан из смысловых слов. Мы начали с того, что стали случайным образом подставлять слово the в открытый текст и определять соответствующие буквы ключа. Мы могли с уверенностью сказать, когда the попадает на надлежащее место, потому что буквы ключа в этом случае приобретали вид части смысловых слов. После чего мы использовали эти фрагменты в ключе, чтобы определить слова целиком. А это, в свою очередь, давало нам больше кусков в тексте, из которых мы могли составить целые слова, и так далее. Весь этот процесс переходов вперед-назад между сообщением и ключом оказался возможен только потому, что у ключа была определенная внутренняя структура и он состоял из слов, которые можно было распознать. Однако в 1918 году криптографы начали экспериментировать с ключами, которые были лишены структуры. В результате получился невзламываемый шифр.

Когда Первая мировая война уже приближалась к концу, майор Джозеф Моборн, руководитель криптографического исследовательского подразделения армии США, ввел понятие случайного ключа, т. е. такого ключа, который состоит не из распознаваемого набора слов, а из случайной комбинации букв. Он высказывался за применение таких случайный ключей, используемых как часть шифра Виженера, для обеспечения беспрецедентной степени стойкости. Первым этапом в системе Моборна была подготовка толстого блокнота, состоящего из сотен бумажных листов; на каждом листе находится уникальный ключ в виде случайной последовательности строчек букв. Подготавливаются два экземпляра блокнота, один для отправителя, а второй — для получателя. Чтобы зашифровать сообщение, отправитель применял шифр Виженера, пользуясь первым листом блокнота в качестве ключа. На рисунке 30 показаны три листа из такого блокнота (на самом деле, на каждом листе содержатся сотни букв) и сообщение, зашифрованное с использованием случайного ключа, находящегося на первом листе. Получатель сможет легко расшифровать шифртекст, пользуясь идентичным ключом и шифром Виженера. После того как сообщение было успешно отправлено, получено и расшифровано, оба — и отправитель, и получатель — уничтожают лист, использованный в качестве ключа, чтобы никогда уже больше им не пользоваться. При шифровании очередного сообщения применяется следующий случайный ключ из блокнота, который в дальнейшем также уничтожался, и так далее. Поскольку каждый лист используется только один раз, эта система известна как одноразовый шифрблокнот, или шифрблокнот одноразового назначения[15].

_{Рис. 30 Три листа из одноразового шифрблокнота, каждый из которых является возможным ключом для шифра. Сообщение зашифровано с помощью листа 1.}

Шифр из одноразового шифрблокнота свободен от всех вышеозначенных слабостей. Представим, что сообщение attack the valley at dawn было зашифровано, как показано на рисунке 30, передано по радио и перехвачено противником.

Криптоаналитик противника получает шифртекст и пытается дешифровать его. Первый камень преткновения: по определению в случайном ключе повторений нет, поэтому методом Бэббиджа и Касиски взломать криптографический ключ одноразового использования не удастся. Как вариант, криптоаналитик противника может попытаться подставлять слово the в различные места текста и определять соответствующий фрагмент ключа, как это делали мы, когда старались дешифровать предыдущее сообщение. Если криптоаналитик попробует поставить the в начале сообщения, что неверно, тогда соответствующий сегмент ключа будет иметь вид WXB, иначе говоря, он получит хаотичный набор букв. Если же криптоаналитик подставит the таким образом, что начало слова будет совпадать с седьмой буквой сообщения, то есть в нужное место, тогда соответствующий сегмент ключа будет иметь вид QKJ, что также является беспорядочным набором букв. Другими словами, криптоаналитик не сумеет определить, на своем месте стоит пробное слово или нет.

В отчаянии криптоаналитик мог бы даже подумывать о поиске методом полного перебора всех возможных ключей. Шифртекст состоит из 21 буквы, так что криптоаналитик знает, что и ключ также состоит из 21 буквы. Это означает, что следует проверить примерно 500 000 000 000 000 000 000 000 000 000 возможных ключей, что абсолютно неосуществимо ни для человека, ни для механического устройства. Однако даже если криптоаналитик смог бы проверить все эти ключи, то в этом случае возникнет еще более значительная сложность. Проверяя каждый возможный ключ, криптоаналитик, несомненно, обнаружит истинное сообщение, но будут также представлены и все ложные сообщения. Так, например, если применить к предыдущему шифртексту следующий ключ, то получится совершенно иное сообщение:

Если бы мог быть проверен каждый возможный ключ, то при этом будут появляться все мыслимые и немыслимые сообщения длиной в 21 букву, и криптоаналитик не сумел бы отличить истинное сообщение от всех остальных. Этой проблемы не возникло бы, если бы ключ представлял собой набор слов или фразу, поскольку неправильные сообщения почти наверняка будут связаны с не имеющими смысла ключами, а истинное сообщение будет получено при осмысленном ключе.

Стойкость шифра одноразового шифрблокнота целиком и полностью обусловлена случайным характером ключа. Ключ вносит разупорядоченность в шифртекст, и если шифртекст является неупорядоченным, то нет никаких закономерностей, никакой структуры, — ничего, за что мог бы зацепиться криптоаналитик. В действительности можно математически доказать, что криптоаналитик не сможет вскрыть сообщение, зашифрованное с помощью шифра из одноразового шифрблокнота. Другими словами, шифр одноразового шифрблокнота не просто считается невзламываемым, как считался невзламываемым шифр Виженера в девятнадцатом веке, он на самом деле абсолютно надежен. Одноразовый шифрблокнот гарантирует стойкость — воистину Святой Грааль криптографии.

Наконец-то криптографы нашли невзламываемую систему шифрования. Однако безупречность шифра одноразового шифрблокнота не означает, что поиск обеспечения стойкости на этом закончился: дело в том, что им пользовались крайне редко. Хотя он теоретически и совершенен, но в действительности ему присущи две принципиальные сложности. Во-первых, на практике затруднительно создавать большое количество случайных ключей. В самый обычный день в армии могут передавать и получать сотни сообщений, каждое из тысяч знаков, поэтому радистам потребуется дневной запас ключей, эквивалентный миллионам расположенных в случайном порядке букв. А это исключительно сложная задача — создание такого колоссального количества случайных последовательностей букв.

Ранее некоторые криптографы полагали, что они могут создать огромное количество случайных ключей, наобум печатая на печатной машинке. Однако при этом машинистка (или оператор печатающего устройства) всякий раз стремилась печатать буквы следующим образом: одну букву левой рукой, следующую — правой и так далее, поочередно ударяя по клавишам то на одной, то на другой стороне. Таким способом и в самом деле можно было быстро создать ключ, но получающаяся при этом последовательность обладала структурой и вследствие этого более не являлась случайной — если машинистка ударяла по клавише с буквой D, находящейся на левой части клавиатуры, то следующей буквой, скорее всего, будет буква, находящаяся на правой части клавиатуры. Если же криптографический ключ одноразового использования действительно случаен, то примерно в половине всех случаев за буквой с левой части клавиатуры должна следовать другая буква с левой же части клавиатуры.

Криптографы осознали, что для создания случайного ключа потребуется много времени, сил и средств. Лучшие случайные ключи создаются на основе естественных физических процессов, например, радиоактивности, которая, как известно, действительно имеет случайный характер. Криптограф может взять крупный кусок радиоактивной руды и измерять излучение с помощью счетчика Гейгера. Иногда ионизирующие частицы излучения испускаются одна за одной очень быстро, иногда между отдельными актами испускания проходит довольно длительное время, поэтому время между этими актами есть величина непредсказуемая и случайная. В таком случае криптограф может подсоединить к счетчику Гейгера дисплей, на экране которого в циклическом режиме быстро, но с постоянной скоростью пробегает алфавит, моментально останавливающийся при срабатывании счетчика. Какой бы ни была буква на экране, она может использоваться в качестве очередной буквы случайного ключа. После этого на экране дисплея опять начинается пролистывание алфавита в циклическом режиме до следующего срабатывания счетчика, которое происходит в результате попадания в него ионизирующей частицы; замершая на экране буква добавляется к ключу, и процесс идет далее. Такое устройство гарантированно создавало бы действительно случайный ключ, но оно непригодно для повседневной криптографии.

Даже если бы вы смогли создать достаточно случайные ключи, то возникла бы еще одна проблема: сложность их распределения. Представьте себе район боевых действий, где сотни радистов составляют единую коммуникационную сеть. Для начала все они должны иметь идентичные экземпляры одноразового шифрблокнота. Затем, когда подготовлены новые шифрблокноты, их необходимо одновременно передать всем. Наконец, все должны быть уверены, что нужный лист одноразового шифрблокнота используется в нужное время. При широком применении одноразовых шифрблокнотов на поле боя будет просто столпотворение курьеров и писарей. Более того, если противник захватит хотя бы один комплект ключей, то надежность всей коммуникационной системы будет нарушена.

Представляется соблазнительным сократить усилия на подготовку и распределение ключей путем повторного использования одноразовых шифрблокнотов, но это смертный грех криптографии.

Повторное использование одноразового шифрблокнота позволит криптоаналитику противника легко дешифровать сообщения. Принцип, с помощью которого вскрываются два фрагмента шифртекста, зашифрованного одним и тем же криптографическим ключом одноразового использования, объясняется в Приложении G, но пока следует запомнить, что в использовании одноразового шифрблокнота нельзя делать никаких упрощений. Для каждого сообщения отправитель и получатель должны использовать новый ключ.

Одноразовый шифрблокнот полезен только тем, кому нужна сверхнадежная связь и кто может позволить себе заплатить огромную цену за создание и надежное распределение ключей. Например, безопасность телефонной «горячей линии» между президентами России и Америки обеспечивается посредством использования одноразового шифрблокнота.

Практические недостатки теоретически совершенного одноразового шифрблокнота означали, что идею Моборна никогда не удастся применить в разгаре сражения. По окончании Первой мировой войны и всех криптографических неудач продолжался поиск практичной системы, которую можно было бы применить в следующем конфликте. К радости криптографов это продолжалось недолго; вскоре они совершили прорыв, благодаря которому была восстановлена надежность связи на поле сражения. Чтобы упрочить свои шифры, криптографы, для обеспечения криптостойкости при зашифровывали сообщений, были вынуждены отказаться от использования бумаги и карандаша и применять самые последние достижения.