Гуси, которые никогда не гоготали
В течение тринадцати лет англичане и французы полагали, что шифр «Энигмы» взломать нельзя, но теперь появилась надежда. Поляки продемонстрировали, что в шифре «Энигмы» имеются изъяны, и это подняло моральный дух криптоаналитиков-союзников. Движение вперед поляков застопорилось с внедрением новых шифраторов и дополнительных кабелей штепсельной коммутационной панели, но было доказано, что шифр «Энигмы» больше не может считаться совершенным.
Достижения поляков послужили для союзников доказательством необходимости привлечения к работе математиков в качестве дешифровальщиков. В Британии, в «Комнате 40», всегда преобладали лингвисты и знатоки классических языков, но теперь совместными усилиями в штате стали появляться математики и ученые. Их приглашали главным образом через однокашников, тех, с кем ранее они учились в Оксфордском и Кембриджском университетах. На работу в «Комнату 40» приглашали также и выпускниц Ньюнем-колледжа и Гиртон-колледжа Кембриджского университета.
Вновь пришедших сотрудников направляли не в «Комнату 40» в Лондоне, а в Блечли-Парк, находящийся в графстве Бакингемшир, где располагалась правительственная школа кодов и шифров — организация, которая была не столь давно образована из «Комнаты 40» и занималась дешифрованием сообщений. В отличие от «Комнаты 40», в Блечли-Парке могло разместиться гораздо больше сотрудников, что было существенно, поскольку, как только начнется война, ожидалась просто лавина перехваченных зашифрованных сообщений. В Первую мировую войну Германия передавала два миллиона слов в месяц, однако во Второй мировой войне, вследствие широкого использования радиосвязи, эти два миллиона слов могли бы передаваться за день.
В центре Блечли-Парка стоял большой викторианский особняк в стиле тюдоровской готики, построенный сэром Гербертом Леоном, финансовым магнатом девятнадцатого столетия. Этот особняк, с его библиотекой, обеденным и изысканно убранным бальным залом, обеспечил центральную администрацию всем, что нужно для работы в Блечли. У капитана 3-го ранга Аластера Деннистона, руководителя правительственной школы кодов и шифров, был кабинет на первом этаже, из окон которого открывался прекрасный вид на сады; к сожалению, этот вид был вскоре испорчен строительством многочисленных казарм. В этих временных деревянных постройках были размещены различные дешифровальные службы и подразделения. Так, казарма 6 специализировалась на вскрытии немецких армейских сообщений, зашифрованных с помощью «Энигмы». Дешифрованные сообщения из казармы 6 передавались в казарму 3, где оперативные сотрудники разведки переводили их и старались использовать полученную информацию. Казарма 8 специализировалась на «Энигме» военно-морских сил; свои дешифровки они передавали на перевод и использование разведданных в казарму 4. Первоначально в Блечли-Парке насчитывалось всего двести человек, но за пять лет численность мужчин и женщин, размещающихся в особняке и казармах, возросла до семи тысяч.

Рис. 44 В августе 1939 года ведущие дешифровальщики Британии приехали в Блечли-Парк, чтобы оценить, насколько он подходит в качестве места для новой правительственной школы кодов и шифров. Чтобы не вызывать подозрений местных жителей, они выдавали себя за группу охотников капитана Ридли.
За осень 1939 года ученые и математики в Блечли изучили хитросплетения шифра «Энигмы» и быстро овладели методом поляков. В сравнении с польским Бюро шифров в Блечли было больше сотрудников и больше ресурсов, и поэтому здесь могли справиться с большим числом расположений шифраторов и с тем, что «Энигму» теперь взломать стало в десять раз труднее. Каждый день британским дешифровальщикам приходилось выполнять одну и ту же процедуру. В полночь немецкие операторы «Энигмы» меняли ключ текущего дня на новый, и с этого момента все, чего достигли в Блечли в предыдущий день, пропадало втуне: дешифровать сообщения не удавалось. Дешифровальщики опять были вынуждены начинать поиск нового ключа текущего дня. Это могло занимать несколько часов, но как только становились известны установки «Энигмы» на текущий день, в Блечли тут же приступали к дешифрованию накопившихся за это время немецких сообщений, извлекая из них информацию, которая была просто бесценной для повышения обороноспособности страны.
Для любого, военачальника неожиданность является неоценимым козырем. Но после того, как в Блечли смогли взломать «Энигму», планы немцев стали ясны и англичане смогли заранее узнавать намерения немецкого верховного командования. Так, зная о предстоящем наступлении, можно было послать туда подкрепление или предпринять маневры, чтобы уклониться от столкновения. Союзникам, сумевшим дешифровать переговоры немцев о слабостях собственных позиций, представлялась возможность предпринимать там свои наступательные операции. Поэтому дешифровки Блечли были исключительно важны. Например, когда в апреле 1940 года Германия вторглась в Данию и Норвегию, в Блечли дали детальную картину немецких действий.
Точно так же во время битвы за Англию[17] криптоаналитики могли заблаговременно предупреждать о налетах бомбардировщиков, указывая, в том числе, время и место налета. Они могли также постоянно информировать о состоянии Люфтваффе, к примеру, о потерях самолетов и о том, с какой скоростью происходила их замена. Из Блечли вся эта информация поступала в штаб-квартиру МИ6 (британская служба внешней разведки), откуда ее направляли далее в военное министерство, в министерство ВВС и в Адмиралтейство.
Однако иногда, в перерывах между своими усилиями влиять на ход войны, криптоаналитики находили время и для отдыха. Как писал Малькольм Маггеридж, сотрудник секретной службы, посещавший Блечли, излюбленным их развлечением была английская лапта:
Каждый день после обеда, если погода благоприятствовала, взломщики шифров играли в английскую лапту на лужайке у особняка с притворной серьезностью, которую напускают на себя университетские преподаватели, занимаясь чем-то, что они считают пустячным или малозначительным по сравнению с их более важными исследованиями. Так, они спорили о каких-то моментах игры с той же страстью, с какой могли бы обсуждать вопрос о свободе воли и детерминизме или о теории происхождения Вселенной — в результате ли «большого взрыва», или же то был процесс непрерывного созидания.

Рис. 45 Дешифровальщики Блечли за игрой в английскую лапту.
Овладев методом поляков, криптоаналитики Блечли начали придумывать свои собственные ускоренные способы поиска ключей «Энигмы». Например, они обратили внимание на тот факт, что немецкие операторы «Энигмы» время от времени выбирали разовые ключи, которые никак нельзя было назвать случайными. Для каждого сообщения оператор должен был выбирать разовый ключ с тремя случайными буквами. Однако в пылу сражения перегруженные работой операторы иногда набирали на клавиатуре «Энигмы» три последовательно идущие буквы (рис. 46) — QWE или BNM. Такие предсказуемые разовые ключи были названы силями (cillies). Другой тип си-лей — это неоднократное использование одного и того же разового ключа, к примеру, инициалов любимой девушки оператора; вполне возможно, что один из таких инициалов — C.I.L. — как раз и послужил в качестве источника этого названия. Перед тем как приступать к трудоемкому процессу взламывания шифра «Энигмы», для криптоаналитиков стало обычным делом сначала проверять наличие силей, и иногда их интуиция давала свои плоды.

Рис 46. Клавиатура «Энигмы»
Сили не были слабым местом «Энигмы», они, скорее, являлись слабостью способа ее использования. Стойкость шифра «Энигмы» снижается также и из-за человеческих ошибок на более высоких уровнях. Те сотрудники, которые отвечают за составление шифровальных книг, должны решать, какие из шифраторов в какой день следует использовать и каково должно быть их расположение. Они стремились обеспечить случайные, непредсказуемые установки шифраторов, чтобы ни один из шифраторов не оставался на одном и том же месте два дня подряд. Так, если мы обозначим шифраторы номерами 1, 2, 3, 4 и 5, то в первый день их расположение может быть таким — 134, а на второй день — 215, но не 214, поскольку шифратор с номером 4 не должен оставаться в том же положении в течении двух дней подряд. Это, на первый взгляд, здравый подход, ведь шифраторы постоянно меняются местами, но на самом деле применение такого правила облегчает жизнь криптоаналитика.
Исключение определенных расположений, чтобы шифраторы не оставались на тех же самых местах, означает, что составители шифровальных книг наполовину уменьшают число возможных расположений шифраторов. Криптоаналитики Блечли осознали эту ситуацию и извлекли из нее максимальную пользу. Определив расположение шифраторов в какой-то из дней, они могли сразу же исключить половину возможных расположений шифраторов на следующий день. Тем самым объем их работы снижался вдвое.
Точно так же существовало правило, согласно которому не допускалась перестановка соседних букв с помощью штепсельной коммутационной панели, то есть S могла меняться местами с любой буквой, кроме K и T. Теоретически таких очевидных перестановок следовало избегать, но применение этого правила приводило опять-таки к существенному сокращению количества возможных ключей.
Поскольку «Энигма» продолжала усовершенствоваться и во время войны, то был необходим и поиск новых криптоаналитических ускоренных методов. Криптоаналитики были постоянно вынуждены модернизировать и совершенствовать «бомбы» и разрабатывать полностью новые подходы. Частично их успех заключался в причудливом сочетании математиков, ученых, лингвистов, знатоков классических языков, шахматных гроссмейстеров и любителей кроссвордов в каждой из казарм. Трудноразрешимая задача передавалась из казармы в казарму, пока не находился тот, кто мог ее решить, или хотя бы тот, кто сумеет решить ее частично, после чего ее передавали дальше Гордон Уэлчман, являвшийся руководителем казармы 6, говорил о своей команде как о «своре гончих, старающихся отыскать запах». Здесь трудилось множество великих криптоаналитиков, и они добились значительных успехов, но чтобы подробно описать вклад каждого из них, потребовалось бы несколько толстых томов. Однако если и была какая-то фигура, которую следовало бы отметить, так это Алан Тьюринг, который сумел отыскать самое слабое место в шифре «Энигмы» и воспользовался им. Благодаря Тьюрингу стало возможным взломать шифр «Энигмы» даже в таких крайне сложных обстоятельствах.
Алан Тьюринг был зачат осенью 1911 года в Чатрапуре, городе недалеку от Мадраса в южной Индии, где его отец, Джулиус Тьюринг, состоял на государственной гражданской службе. Джулиус и его жена Этель решили, что их сын должен родиться в Англии, и вернулись в Лондон, где 23 июня 1912 года родился Алан. Вскоре после рождения сына отец возвратился в Индию, а спустя пятнадцать месяцев за ним последовала и мать, оставив Алана на попечении нянь и друзей, пока он не подрос настолько чтобы его можно было отдать в школу-интернат.
В 1926 году четырнадцатилетний Алан Тьюринг стал учеником Шербурнской школы в графстве Дорсет. Начало его первого семестра совпало с общенациональной стачкой, но Тьюринг был полон решимости прибыть на занятия в первый же день и ради этого проехал 100 км от Саутгемптона до Шербурна на велосипеде — подвиг, который был отмечен в местной печати. К концу первого года обучения в школе Тьюринг приобрел репутацию трудного ребенка, интересующегося только наукой. Цель Шербурнской школы заключалась в том, чтобы сделать из детей широко образованных и гармонично развитых людей, годных для управления империей, но Тьюринг к этому не стремился, а преподаваемые предметы оставляли его равнодушным.
Его единственным настоящим другом в Шербурнской школе стал Кристофер Морком, который, как и Тьюринг, был всецело предан науке. Вместе они обсуждали последние научные новости, вместе проводили свои эксперименты. Их близость подогревала любознательность Тьюринга, но она, что более важно, оказала на него также и глубокое эмоциональное воздействие. Эндрю Ходжес, биограф Тьюринга, писал: «…это была первая приязнь, первая симпатия… Она способствовала озарению ума, словно вспышка искрящийся и переливающийся всеми цветами радуги в черно-белом мире». Их дружба длилась четыре года, но, похоже, Морком не осознавал всей глубины чувств, которые испытывал к нему Тьюринг. А в последний год пребывания в Шербурне Тьюринг навсегда утерял возможность сказать ему о них. 13 февраля 1930 года, в четверг, Кристофера Моркома не стало; он внезапно умер от туберкулеза.
Тьюринг был подавлен потерей единственного человека, которого искренне полюбил. Чтобы хоть как-то смириться со смертью Моркома, он целиком сосредоточился на научных исследованиях в попытке реализовать потенциал своего друга. Морком, который, по всей видимости, был более одарен, уже сдал экзамены в Кембриджский университет и получил стипендию. Тьюринг считал своим долгом также поступить в Кембридж, а затем совершить открытия, которые при других обстоятельствах сделал бы его друг. Он попросил мать Кристофера прислать ему фотографию и, когда получил ее, написал ответ, поблагодарив ее: «Теперь она стоит на моем столе, побуждая меня усиленно трудиться».

Рис. 47 Алан Тьюринг.
В 1931 году Тьюринг поступил в Королевский колледж Кембриджа. Он приехал, когда шли жаркие дискуссии о природе математики и логики, и его окружали некоторые из великих людей того времени: Бертран Рассел, Альфред Норт Уайтхед и Людвиг Витгенштейн. В центре споров была статья логика Курта Геделя о неразрешимости. Всегда считалось, что, по крайней мере в теории, на все математические вопросы можно найти ответ. Однако Гедель показал, что могут существовать задачи, которые нельзя решить логическим путем, так называемые неразрешимые задачи. Математики были потрясены новостью, что, оказывается, математика не так уж всесильна, как они всегда считали. Они попытались спасти свою науку, постаравшись отыскать способ выявления неудобных неразрешимых задач с тем, чтобы суметь надежно избавиться от них. Именно эта цель в конце концов вдохновила Тьюринга написать свою самую важную математическую статью «О вычислимых числах», опубликованную в 1937 году. В пьесе «Взлом шифра» Хью Уайтмора о жизни Тьюринга кто-то спросил Алана о значении его статьи. Тот ответил: «Она об истинном и ложном. В общем смысле. Это специальная статья о математической логике, но она также и о сложности отделения истины от ошибочного высказывания. Люди, причем большинство, считают, что в математике мы всегда знаем, что истинно, а что ложно. Это отнюдь не так. Больше не так».
В своей статье Тьюринг постарался идентифицировать неразрешимые задачи и дал описание воображаемой машины, которая предназначается для осуществления конкретной математической операции, или алгоритма. Другими словами, машина может выполнять определенную, заранее установленную последовательность шагов, в процессе которых будет происходить, к примеру, умножение двух чисел. Тьюринг полагал, что перемножаемые числа могли бы поступать в машину на бумажной ленте, наподобие ленты с дырочками, служащей для игры пианолы. Результат умножения будет выводиться на другой ленте. Его воображению рисовался целый ряд таких так называемых машин Тьюринга, каждая из которых специально предназначена для выполнения определенной задачи, например, деления, возведения в квадрат или разложения на множители. Затем Тьюринг предпринял еще более радикальный шаг.
Он представил себе машину, работу которой можно менять, благодаря чему она сможет выполнять все действия всех возможных машин Тьюринга. Изменения будут производиться путем ввода тщательно подготовленных лент, которые превращают универсальную машину в машину для деления, машину для умножения или в машину любого другого типа. Тьюринг назвал такое гипотетическое устройство универсальной машиной Тьюринга, так как она была способна дать ответ на любой вопрос, на который можно было бы дать логический ответ. К сожалению, как оказалось, не всегда можно логически ответить на вопрос о разрешимости или неразрешимости другой задачи, и поэтому даже универсальная машина Тьюринга не могла определить каждую неразрешимую задачу.
Математики, прочитав статью Тьюринга и узнав, что укротить монстра Геделя так и не удалось, были разочарованы, однако в качестве утешительного приза они получили от Тьюринга концепцию современного программируемого компьютера. Тьюринг знал о работе Бэббиджа, так что универсальная машина Тьюринга могла бы рассматриваться как реинкарнация разностной машины № 2[18]. На самом же деле Тьюринг пошел гораздо дальше, — он заложил прочные теоретические основы программирования, благодаря чему у вычислительных машин появились немыслимые доселе возможности. Но это были 30-е годы, и технологии, способной помочь воплотить универсальную машину Тьюринга в реальность, пока еще не существовало. Однако Тьюринга вовсе не беспокоило, что его теории намного опередили технические возможности его времени. Он просто хотел получить признание со стороны математического сообщества, которое восприняло его статью как поистине одно из наиболее крупнейших достижений столетия. На тот момент ему исполнилось всего лишь двадцать шесть.
То был самый счастливый и успешный период жизни Тьюринга. К этому времени его избрали членом научного общества Королевского колледжа, ставшего родным домом для цвета мировой интеллектуальной элиты. Он вел жизнь типичного кембриджского преподавателя, сочетающего занятия «чистой» математикой с повседневной деятельностью. В 1938 году он с увлечением посмотрел фильм «Белоснежка и семь гномов», где на него произвела неизгладимое впечатление сцена, когда злая колдунья макает яблоко в яд. После коллеги неоднократно слышали, как Тьюринг напевал: «В напиток яблоко макнешь и навеки ты уснешь».
Годы в Кембридже для Тьюринга остались незабываемы. Помимо успехов на научном поприще, среда, в которой он очутился, отличалась благожелательностью и терпимостью. В университете был широко распространен гомосексуализм; здесь можно было свободно вступать в связь, не тревожась о том, обнаружит ли это кто-нибудь и что об этом скажут. Хотя у Тьюринга не было ни с кем длительных серьезных отношений, он казался доволен жизнью. Но в 1939 году академическая карьера Тьюринга внезапно завершилась. Правительственная школа кодов и шифров пригласила его в качестве криптоаналитика в Блечли, и 4 сентября 1939 года, на следующий день после того, как Невилл Чемберлен объявил Германии войну, Тьюринг перебрался из роскоши Кембриджа в гостиницу Кроун Инн в Шенли Брук Энде.
Каждый день он садился на велосипед и ехал 5 километров от Шенли Брук Энда до Блечли-Парка, где проводил часть времени в казармах, выполняя обыденную дешифровальную работу, а часть — в «мозговом центре» Блечли, занимающем помещение, где раньше у сэра Герберта Леона хранились яблоки, груши и сливы. Этот «мозговой центр», — группа ведущих ученых, — собирался в тех случаях, когда криптоаналитикам предстояло разрешить вставшие перед ними новые проблемы или спрогнозировать, какие проблемы могут возникнуть в будущем. Задача Тьюринга заключалась в том, чтобы понять, как поступать, если в немецкой армии изменится система обмена разовыми ключами. Прежний успех в Блечли был достигнут благодаря работе Реевского, которая опиралась на тот факт, что операторы Энигмы зашифровывали каждый разовый ключ дважды (например, при разовом ключе YGB оператор будет его зашифровывать как YGBYGB). Считалось, что такое повторение гарантирует получателя от ошибок, но оно же создавало брешь в надежности Энигмы. Британские криптоаналитики полагали, что это не сможет продлиться долго, что немцы заметят, что повторяющийся ключ компрометирует шифр Энигмы, и тут же операторам Энигмы будет предписано отказаться от его повторения, а это приведет к тому, что применяемые в Блечли способы дешифрования с этого момента окажутся бесполезными. Задача Тьюринга как раз и заключалась в том, чтобы отыскать альтернативный путь атаки Энигмы без использования повторяющегося разового ключа.
Несколько недель спустя Тьюринг узнал, что в Блечли накоплена обширная библиотека дешифрованных сообщений. Ознакомившись с ними, он заметил, что многие из них имеют неизменную структуру, благодаря чему, как он полагал, ему иногда удавалось бы предсказать часть содержания недешифрованного сообщения, зная только, когда и откуда оно было отправлено. Так, исходя из накопленною опыта, он знал, что немцы ежедневно в 6 утра или чуть позже посылали обычную зашифрованную сводку погоды. Поэтому в зашифрованном сообщении, перехваченном в 6.05 утра, почти наверняка будет присутствовать слово wetter — немецкое слово «погода». Скрупулезное следование правилам в любой военной организации означало, что по стилю такие сообщения были жестко регламентированы, так что Тьюринг был уверен даже в том, где именно в зашифрованном сообщении стоит слово wetter. Его опыт мог подсказать ему, что буквам открытого текста wetter соответствуют первые шесть букв некоторого зашифрованного текста. Когда часть открытого текста может быть сопоставлена части шифртекста, то такое сочетание называется крибом[19].
Тьюринг был уверен, что теперь он сможет использовать крибы, чтобы разгадать «Энигму». Если бы у него был шифртекст и он бы знал, что некоторая его часть, к примеру, ETJWPX, является словом wetter, то задача состояла бы в том, чтобы найти такие установки «Энигмы», при которых wetter преобразуется в ETJWPX. Прямой, но в действительности неосуществимый способ — криптоаналитик берет «Энигму», вводит слово wetter и смотрит, появится ли правильный шифртекст.
Если нет, то он меняет установки машины, меняя местами кабели на штепсельной коммутационной панели, переставляя шифраторы или изменяя их положение, а затем снова вводит слово wetter. Если правильный шифртекст не появляется, криптоаналитик снова меняет установки и повторяет это до тех пор, пока не получит правильный шифртекст. Единственная проблема при использовании такого метода проб и ошибок заключается в том, что необходимо проверить 159 000 000 000 000 000 000 возможных установок, так что найти такую установку, при которой wetter будет преобразована в ETJWPX, является, похоже, невыполнимой задачей.
Чтобы упростить данную ситуацию, Тьюринг попробовал следовать стратегии Реевского. Он хотел разделить задачу поиска установок шифраторов (какой из шифраторов в каком пазу расположен, и как они сориентированы относительно друг друга) от задачи, связанной с поиском расположения кабелей на штепсельной коммутационной панели. Так что если бы он сумел найти участок в крибе, на котором не сказывается расположение кабелей на штепсельной коммутационной панели, то ему оказалось бы вполне по силам проверить каждую из оставшихся 1 054 560 возможный комбинаций положений шифраторов (60 расположений x 17 576 ориентаций). Найдя нужные установки шифраторов, он смог бы затем определить, как расположены кабели на штепсельной коммутационной панели.
В конце концов, он остановился на особом типе криба, в котором имелись внутренние петли — аналогично цепочкам, которыми воспользовался Реевский. Цепочки Реевского связывали буквы в повторяющемся разовом ключе. Однако петли Тьюринга не имели никакого отношения к разовому ключу, так как он действовал в предположении, что немцы вскоре прекратят их посылать. Вместо этого петли Тьюринга связывали буквы открытого текста и шифртекста в крибе. К примеру, такая петля есть у криба, представленного на рисунке 48.
Вспомним, что крибы — это только предположения, но если мы допустим, что данный криб правилен, то мы можем связать в виде части петли буквы w — > E, e — > T, t — > W. Хотя мы ничего не знаем об установках «Энигмы», мы можем обозначить первое положение, каким бы оно ни было, как S. Как мы знаем, в первом положении w зашифровывается как E. После того как произойдет зашифровывание, первый шифратор повернется на один шаг и перейдет в положение S+1, в котором буква e зашифровывается как T. Шифратор снова переместится на один шаг вперед и произведет зашифровывание буквы, которая не является частью петли, поэтому это зашифровывание мы не рассматриваем. Далее шифратор переместится вперед еще на один шаг, и мы вновь приходим к букве, которая является частью петли. Нам известно, что в положении S+3 буква t зашифровывается как W. Итак, мы знаем, что:
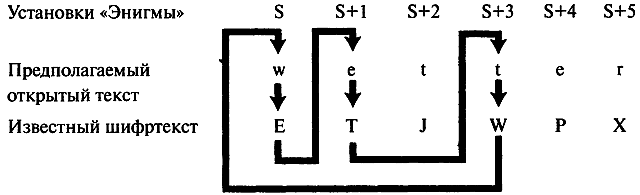
Рис. 48 Один из крибов Тьюринга, имеющий петлю.
В положении S, «Энигма» зашифровывает w как E.
В положении S+1, «Энигма» зашифровывает e как T.
В положении S+3, «Энигма» зашифровывает t как W.
Пока что такая петля представляется ничем иным, кроме как любопытной структурой, но Тьюринг неукоснительно придерживался связей в петле и обнаружил, что они существенно облегчают ему задачу взлома «Энигмы». Вместо того чтобы задействовать только одну «Энигму» для проверки каждой установки, Тьюринг представил себе три отдельно работающие шифровальные машины, каждая из которых осуществляет зашифровывание только одного элемента петли. Первая машина будет стремиться зашифровать w как E, вторая — e как T, а третья — t как W. Все эти три машины будут иметь идентичные установки, за исключением того, что у второй машины ориентация шифратора будет соответствовать положению, обозначенному как S+1, то есть относительно первой машины он будет находиться на один шаг впереди, а у третьей машины ориентация шифратора будет соответствовать положению, обозначенному как S+3, то есть относительно первой машины он будет находиться на три шага впереди. Тьюринг затем вообразил доведенного до безумия криптоаналитика, непрерывно меняющего расположение кабелей на штепсельной коммутационной панели, переставляющего местами шифраторы и изменяющего их ориентацию, чтобы получить нужный шифртекст. Как бы ни менялись кабели на первой машине, их следовало таким же образом поменять и на двух других. Как бы ни менялось расположение шифраторов на первой машине, их следовало точно так же изменить и на двух других. И, что принципиально, какова бы ни была ориентация шифратора на первой машине, шифраторы на второй и третьей машинах должны иметь эту же ориентацию, только на второй — повернутым вперед на один шаг, а на третьей — на три шага.
Казалось бы, что Тьюринг добился немногого. Криптоаналитику, как и прежде, необходимо будет проверять все 159 000 000 000 000 000 000 возможных установок, но в довершение всего теперь он должен делать это одновременно на трех машинах вместо одной. Однако на следующем этапе Тьюринг видоизменил задачу и существенно упростил ее. Он представил, что входы и выходы всех трех машин соединены между собой электрическими проводами, как показано на рисунке 49. По сути, петля в крибе соответствует контуру электрической цепи. Тьюринг представил себе машины, меняющие свои соединения на штепсельной коммутационной панели и установки шифраторов, как описано выше, однако цепь станет замкнутой и через машины потечет ток только тогда, когда все установки правильны на всех трех машинах. Если в цепи есть лампочка, то при наличии тока она загорится, показывая, что найдены правильные установки. На данном этапе, чтобы зажглась лампочка, машины по-прежнему должны будут проверять все 159 000 000 000 000 000 000 возможных установок. Однако то, что делалось до сих пор, являлось просто подготовкой к завершающему логическому прыжку, благодаря которому задача одним махом стала в сотню триллионов раз легче.
Тьюринг сконструировал электрическую цепь таким образом, чтобы свести к нулю влияние штепсельной коммутационной панели; тем самым это позволило ему исключить из рассмотрения миллиарды возможных установок на ней. На рисунке 49 представлена следующая картина: на первую «Энигму» подается электрический ток, который течет через шифраторы и поступает к некоторой неизвестной букве; обозначим ее L1. Далее он проходит через штепсельную коммутационную панель, преобразующую L1 в E. Эта буква E подсоединена проводом к букве e на второй «Энигме»; после того как ток пройдет через вторую штепсельную коммутационную панель, она вновь преобразуется в L1. Другими словами, обе эти штепсельные коммутационные панели нейтрализуют друг друга. Точно таким же образом, выходящий из шифраторов на второй «Энигме» ток поступает к L2, которая, после штепсельной коммутационной панели, превращается в T. Эта буква T подсоединена проводом к букве t на третьей «Энигме»; после того как ток пройдет через третью штепсельную коммутационную панель, она вновь преобразуется в L2. Короче говоря, все эти штепсельные коммутационные панели нейтрализуют влияние друг друга, вот почему Тьюринг мог их полностью игнорировать.
Тьюрингу необходимо было только подсоединить выход первой группы шифраторов, непосредственно ко входу второй группы шифраторов, также L1 и так далее. К сожалению, он не знал, какой именно буквой является L1 поэтому ему пришлось подсоединить все 26 выходов первой группы шифраторов ко всем 26 соответствующим входам на второй группы и так далее. Фактически, здесь уже насчитывалось 26 электрических контуров, и в каждом имелась лампочка, сигнализирующая о замыкании электрической цепи. Теперь можно было просто проверить каждую из 17 576 ориентаций для всех трех групп шифраторов, принимая во внимание, что вторая группа шифраторов всегда на один шаг опережает первую группу, а третья группа шифраторов находится на два шага впереди второй группы. В конечном итоге, когда будет найдено правильное положение шифраторов, одна из цепей окажется замкнутой и загорится лампочка. Если положение шифраторов изменяется один раз в секунду, то, чтобы проверить все ориентации, потребуется всего лишь пять часов.
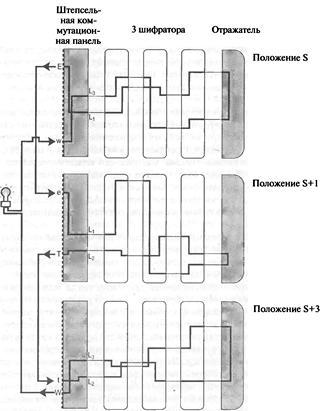
Рис. 49 Петля в крибе может быть представлена как контур электрической цепи. Три «Энигмы» устанавливаются идентично, за исключением того, что у второй машины шифратор повернут на один шаг вперед (положение S+1), а у третьей машины шифратор повернут вперед еще на два шага (положение S+3). Выход каждой «Энигмы» подсоединен ко входу следующей. Три группы шифраторов синхронно вращаются, пощелкивая, пока цепь не замкнется и не загорится лампочка. На приведенном рисунке цепь замкнута, что соответствует искомой установке.
Остались нерешенными только две проблемы. Во-первых, может оказаться так, что на всех трех машинах расположение шифраторов будет неверным, поскольку «Энигма» работает с любыми тремя из имеющихся пяти шифраторов, установленных в любом порядке, что дает шестьдесят возможных способов их расположения. Поэтому если все 17 576 ориентации проверены, а лампочка не загорелась, то следует установить другое из шестидесяти возможных расположений шифраторов и повторять эту операцию до тех пор, пока цепь не окажется замкнутой. Или же у криптоаналитика должно быть шестьдесят комплектов «Энигм» с тремя шифраторами, работающих параллельно.
Вторая задача заключается в том, чтобы после того, как будут определены расположение шифраторов и их ориентация, найти расположение кабелей на штепсельной коммутационной панели. А это уже сравнительно несложно. Установив на «Энигме» требуемое расположение и ориентацию шифраторов, криптоаналитик вводит шифртекст и смотрит на получающийся открытый текст. Если в результате получается tewwer, а не wetter, то ясно, что кабели на штепсельной коммутационной панели должны располагаться таким образом, чтобы осуществлялась перестановка букв w и t. Ввод других отрывков шифртекста позволит определить расположение всех кабелей на штепсельной коммутационной панели.
Только лишь Тьюринг с его исключительным знанием математических машин смог предложить такое сочетание криба, петель и электрически связанных машин. Его воображаемые машины Тьюринга были предназначены для того, чтобы получить ответ на эзотерические вопросы о математической неразрешимости, но благодаря этому чисто академическому исследованию его ум оказался способен спроектировать реально существующую машину для решения вполне практических задач криптоанализа.
В Блечли смогли найти 100 000 фунтов стерлингов, чтобы претворить идею Тьюринга в работающие устройства, которые окрестили «бомбами», поскольку по принципу действия они напоминали «бомбу» Реевского. Каждая из «бомб» Тьюринга состояла из двенадцати электрически связанных шифраторов «Энигма», и могла тем самым справиться с гораздо более длинными петлями букв. В полностью собранном состоянии устройство составляло два метра в высоту, два метра в длину и один метр в ширину. Тьюринг завершил разработку конструкции в начале 1940 года, а заказ на изготовление машины был передан на завод счетно-аналитических машин в Летчворте.
В ожидании, пока доставят «бомбы», Тьюринг продолжал свою ежедневную работу в Блечли. Новости о его победе быстро распространились среди других ведущих криптоаналитиков, которые признали, что он оказался исключительно одаренным дешифровальщиком. По словам Питера Хилтона, его коллеги по работе в Блечли: «Алан Тьюринг был, несомненно, гением, но гением доступным и доброжелательным. Он всегда был готов потратить время и силы, чтобы объяснить свои идеи, однако узким специалистом он не был, — его гибкое мышление охватывало обширную область точных наук».
Впрочем, за пределами Блечли-Парка никто не знал о замечательном достижении Тьюринга, поскольку в правительственной школе кодов и шифров все носило на себе печать высшей формы секретности. К примеру, его родители даже и не подозревали, что Алан был дешифровальщиком, не говоря уже о том, что он был одним из ведущих криптоаналитиков Британии. Как-то раз он сказал своей матери, что его привлекли к военным исследованиям, но в подробности не вдавался. Мать только огорчилась, что это никак не отразилось на ее неряшливо выглядевшем сыне и его прическа не стала более приличной. Хотя руководство в Блечли осуществлялось военными, им пришлось смириться с неряшливостью и экстравагантностью этих «ученых профессоров». Тьюринг редко утруждал себя бритьем, под ногтями у него вечно забиралась грязь, одежда помята. Терпимы ли были военные также и к его гомосексуальности, остается неизвестным. Джек Гуд, ветеран Блечли, заметил: «К счастью, власти не знали, что Тьюринг был гомосексуалистом. В противном случае мы могли бы проиграть войну».
Первый опытный образец «бомбы», который был наречен «Победа», прибыл в Блечли 14 марта 1940 года. Машину сразу же запустили, но первые результаты оказались неудовлетворительными. Она работала гораздо медленнее, чем ожидалось; чтобы отыскать ключ, у нее уходило до недели времени. Объединенными усилиями эффективность «бомб» повысили, и несколькими неделями позже была представлена модифицированная конструкция. Потребовалось еще четыре месяца, чтобы построить усовершенствованную «бомбу». А тем временем криптоаналитикам пришлось столкнуться с той бедой, которую они ожидали. 1 мая 1940 года немцы изменили свой протокол обмена ключами. Они больше не повторяли разовый ключ, и в результате число успешно дешифрованных сообщений резко упало. Информация перестала поступать, и так длилось вплоть до 8 августа, когда прибыла новая «бомба». Эта машина, названная «Agnus Dei», или для краткости «Agnes»[20], должна была удовлетворить всем ожиданиям Тьюринга.
В течение восемнадцати месяцев было изготовлено и запущено в работу еще пятнадцать «бомб», которые исследовали крибы, проверяли установки шифраторов и отыскивали ключи; при этом каждая стучала словно миллион вязальных спиц. Если все шло нормально, «бомба» могла найти ключ «Энигмы» в течение часа. После того, как определены расположение кабелей на штепсельной коммутационной панели и установки шифраторов (разовый ключ) для отдельного сообщения, установить ключ текущего дня не составляет труда. Вслед за этим могут быть дешифрованы и все другие сообщения, отправленные в этот день.
Даже притом, что «бомбы» явились исключительно важным достижением в криптоанализе, дешифрование не превратилось в формальный процесс. Предстояло преодолеть множество препятствий, прежде чем «бомбы» смогли хотя бы приступить к поиску ключа. Так, чтобы привести «бомбу» в действие, вначале понадобится криб. Старшие дешифровальщики выдавали крибы операторам «бомб», но не было никакой гарантии, что дешифровальщики угадали верный смысл шифртекста. И даже при наличии правильного криба, он мог оказаться не на том месте — криптоаналитики смогли догадаться, что зашифрованное сообщение содержит определенную фразу, но сопоставили эту фразу не с тем отрывком шифртекста. Существовал, однако, способ, чтобы проверить, в нужном ли месте находился криб.
Криптоаналитик уверен, что в нижеприведенном крибе открытый текст правилен, но сомневается, правильно ли он сопоставил его соответствующим буквам в шифртексте.
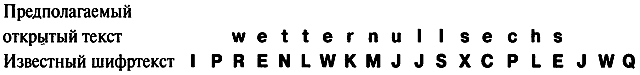
Одна из особенностей «Энигмы» заключалась в том, что она не могла зашифровывать букву саму в себя, что явилось следствием использования отражателя. Буква a никогда не сможет быть зашифрована как A, буква b никогда не сможет быть зашифрована как B и так далее. Поэтому указанный выше криб следует сдвинуть, поскольку первое e в wetter совпадает с E в шифртексте. Чтобы найти нужное выравнивание, мы просто передвигаем открытый текст и шифртекст друг относительно друга до тех пор, пока все буквы в парах букв открытого и шифртекста не станут различными. Если мы сдвинем открытый текст на одну позицию влево, совпадение по-прежнему присутствует, ибо в этом случае первая s в sechs совпадет с S в шифртексте. Однако если мы сдвинем открытый текст на одну позицию вправо, то здесь недопустимых совпадений уже нет.
Так что этот криб стоит, по-видимому, в нужном месте и может использоваться в качестве основы для дешифрования с помощью «бомбы»:
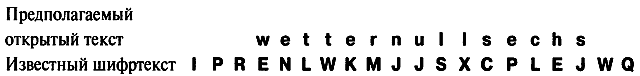
К собранной в Блечли разведывательной информации имели доступ только высшие армейские чины и отдельные члены военного кабинета. Уинстон Черчилль полностью отдавал себе отчет в важности дешифровок, получаемых из Блечли, и 6 сентября 1941 года он посетил дешифровальщиков. Встречая некоторых криптоаналитиков, он был поражен той причудливой смесью людей, которые давали ему ценнейшую информацию: помимо математиков и лингвистов, среди них были специалист по фарфору, смотритель пражского музея, британский чемпион по шахматам и многочисленные знатоки бриджа.
Черчилль проворчал, обращаясь к сэру Стюарту Мензису, руководителю секретной разведывательной службы: «Я велел вам пустить в ход все средства, но не ожидал, что вы поймете меня так буквально». Но несмотря на это он испытывал глубокую нежность к этой пестрой команде, называя их «гусями, откладывающими золотые яйца и никогда не гогочущими».
Этот визит был предназначен для того, чтобы поднять моральный дух дешифровальщиков, показав им, что их работа по достоинству оценена на самом высоком уровне. Вследствие этого визита у Тьюринга и его коллег появилась уверенность, что в случае возникновения кризиса они смогут обратиться к Черчиллю напрямую. Чтобы использовать «бомбы» наилучшим образом, Тьюрингу нужны были еще сотрудники, но все его запросы задерживались капитаном 3 ранга Эдвардом Трэвисом, который стал руководителем Блечли и который чувствовал, что он не смог бы обосновать набор на работу дополнительного количества людей. 21 октября 1941 года криптоаналитики пошли на нарушение субординации и в обход Трэвиса написали прямо Черчиллю:

Рис 50. «Бомба» в действии
Уважаемый премьер-министр! Несколько недель назад Вы оказали нам честь своим визитом, и мы полагаем, что Вы считаете нашу работу важной. Вы видели, что, благодаря в значительной степени энергичным действиям и предусмотрительности капитана 3 ранга Трэвиса, мы вполне обеспечены всем необходимым для создания «бомб» для взлома шифров немецкой «Энигмы». Мы полагаем, однако, что Вам следует знать, что эта работа приостановлена, а в ряде случаев вообще не делается главным образом из-за того, что нам не хватает для этого людей. Причина, по которой мы пишем непосредственно Вам, заключается в том, что в течение месяцев мы делали все от нас зависящее по обычным каналам и что мы потеряли надежду на всякое улучшение положения в ближайшем будущем без Вашего вмешательства…
Покорно Ваши, сэр,
A. М. Тьюринг
B. Г. Уэлчман
К. Х. О’Д. Александер
П. С. Милнер-Барри
Черчилль ответил без промедления. Он сразу же подготовил и передал распоряжение своему офицеру штаба по вопросам личного состава:
ДЕЙСТВИЯ НА ТЕКУЩИЙ ДЕНЬ
В первую очередь удостоверьтесь, что они получили все, что им необходимо, и сообщите мне, что это сделано.
Отныне никаких препятствий для набора персонала и приобретения материалов не возникало. К концу 1942 года уже имелось 49 «бомб», и вскоре в Гэйхерст Мэнор, немного севернее Блечли, появился новый пункт дешифрования. В качестве части кампании по привлечению новых сотрудников правительственная школа кодов и шифров поместила объявление в газете «Дейли Телеграф», в котором читателям газеты был задан вопрос, сможет ли кто-нибудь решить опубликованный кроссворд (рис. 51) менее чем за 12 минут. Считалось, что те, кто хорошо решает кроссворды, также смогут стать и хорошими дешифровальщиками, пополнив ряды «ученых умов», которые уже были в Блечли, но, разумеется, ничего этого в объявлении упомянуто не было. 25 откликнувшихся читателей пригласили для испытания на Флит-Стрит. Пять из них решили кроссворд за заданное время, а еще одному оставалось разгадать последнее слово. Несколькими неделями позже представители военной разведки провели собеседование со всеми шестерыми, и все они были приняты на службу в Блечли-Парк.

Рис. 51 Кроссворд в газете «Дейли Телеграф», использованный в качестве теста при наборе новых дешифровальщиков (решение приведено в Приложении H).
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК