Каковы основные свойства амплитудной модуляции?

При амплитудной модуляции амплитуда несущего колебания А изменяется пропорционально модулирующему сигналу. На рис. 11.1 показаны три колебания — несущее, модулирующее и модулированное. Видно, что в модулированном колебании огибающая выходного сигнала идентична модулирующему сигналу. Характерно то, что, когда огибающая увеличивается в положительном направлении, одновременно она увеличивается и в отрицательном. Амплитуда огибающей является долей амплитуды несущего колебания. Эта доля, обозначаемая буквой m, обычно выражена в процентах и называется коэффициентом глубины модуляции или просто глубиной модуляции. Глубина модуляции может изменяться от 0 до 100 %. Если m больше 100 %, то модулированное колебание сильно искажено.

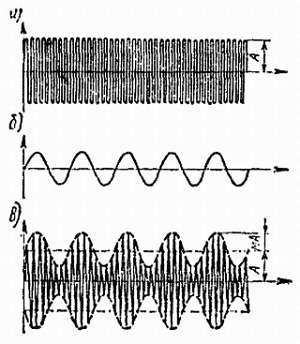
Рис. 11.1. Амплитудная модуляция:

_{а — не модулированное несущее колебание; б — модулирующий сигнал; в — амплитудно-модулированное колебание}

Если несущее колебание промодулировано косинусоидальным сигналом, мгновенное значение модулированного колебания можно записать в следующем виде:

u = (1 + m·cos Ωt)·A·cos ωt

в котором m — глубина модуляции; А — амплитуда несущего колебания; Ω — круговая частота модулирующего сигнала; ω — круговая частота несущего колебания.

Преобразуем это уравнение

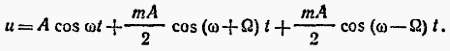
Три полученные составляющие определяют спектр модулированного сигнала.

Первая составляющая является несущим колебанием с частотой ω, вторая составляющая с амплитудой m·А/2 и частотой ω + Ω — верхняя боковая полоса, а третья составляющая с амплитудой m·А/2 и частотой ω — Ω — нижняя боковая полоса. Если, например, частота несущего колебания составляет 200, а частота модулирующего сигнала 1 кГц, то спектр модулированного сигнала состоит из трех частот: 200 кГц, 200 — 1 = 199 кГц и 200 + 1 = 201 кГц.

Из рис. 11.2 видно, что модулирующий сигнал с частотой 1 кГц перенесен в полосу несущей 200 кГц и информация в модулированном сигнале содержится в двух боковых полосах, расположенных симметрично относительно несущего колебания. Одновременно можно сделать вывод, что ширина полосы, занимаемой амплитудно-модулированным сигналом, равна удвоенной частоте модулирующего сигнала.

Рис. 11.2. Частотный спектр амплитудно-модулированного сигнала:

_{1 — несущая частота; 2 — нижняя боковая; 3 — верхняя боковая частота}

Следует подчеркнуть, что существование боковых полос не является результатом математического анализа, вытекающего из преобразования выражения для модулированного сигнала, а имеет реальную физическую интерпретацию. С помощью соответствующих фильтров можно выделить отдельные составляющие спектра, так же как, располагая такими составляющими, можно составить колебание, соответствующее модулированному колебанию.

На практике модулирующий сигнал не является простейшим синусоидальным сигналом, а занимает некоторую полосу частот, например звуковых или изображения. В связи с этим боковые полосы выглядят не одиночными линиями, а полосами, расположенными симметрично относительно несущего колебания.

Из анализа спектра амплитудно-модулированного сигнала вытекает, что полезная информация содержится только в боковых полосах (частотах). Сравнивая амплитуды отдельных спектральных линий, приходим к выводу, что они находятся в соотношении 1:(m/2):(m/2). Поскольку мощность пропорциональна квадрату напряжения, отношение мощностей, переносимых боковыми частотами, имеет вид: 1:(m²/4):(m²/4). Например, если мощность несущего колебания составляет 500 Вт, то при m = 1 мощность каждой из боковых составляет 125 Вт и, следовательно, соответствует только 25 % мощности несущего колебания. При меньших глубинах модуляции доля боковых частот в общей мощности еще меньше. Изменению не подвергается только мощность несущего колебания — переносчик энергии.

Далее увидим, что существует возможность передачи информации без несущего колебания, а также без несущей и одной боковой полосы в системах однополосной модуляции.