§ 3.2 Спектры атомов и атомные модели
§ 3.2 Спектры атомов и атомные модели
Я остался сторонником механистических воззрений XIX столетия и думаю и знаю, что можно объяснить, например, спектральные линии (пока только водорода) без теории Бора, одной ньютоновской механикой.
К.Э. Циолковский [69]
Вальтер Ритц не раз указывал, что ключом к пониманию устройства атома должны стать атомные спектры. И, как было показано выше, Ритц действительно пришёл на основе найденных им спектральных закономерностей к классической модели строения атома. Речь идёт, конечно, не о планетарной модели атома Резерфорда, заведшей в тупик, а о куда менее известной — классической магнитной модели атома, предложенной В. Ритцем в 1908 г. [50] (§ 3.1). По идее Ритца, именно пространственная структура ядра является тем программным центром, который управляет жизнью атома и поведением в нём электронов, подобно тому, как жизнь биологической клетки задана строением клеточного ядра и информационной молекулой ДНК. В магнитной модели ядро управляет полётом электронов посредством магнитных, а не электрических сил. И это естественно: в природе и технике круговое движение электронов создаёт именно магнитная сила, и лишь она объясняет стабильность атома.
Будь движение электронов, как в планетарной модели, вызвано силой Кулона, они неслись бы по орбитам со скоростями порядка скорости света c и мигом (за 10–10 с) падали бы на ядро, растратив энергию на излучение. Магнитные силы меньше электрических и позволяют электронам кружиться гораздо медленней и дольше терять энергию. В самом деле, из магнитной модели, как покажем (§ 3.3, § 4.3), следует открытая Планком связь энергии электрона на орбите
E=MV2/2=hf,
с частотой его обращения f, где h — постоянная Планка. Сократив на MV/2, найдём
V=2hf/MV=h/?Mr,
где r — радиус орбиты электрона. Если r порядка радиуса атома (10–10 м), то V=2300 км/с. Эта скорость, обычная для электронов в лучевых трубках и лампах, на два порядка меньше c. Тогда, связанное с вращением ускорение a=V2/r меньше уже на четыре порядка, радиационное торможение — мало, и электрон на орбите атома живёт долго. Если ж учесть, что в магнитном поле вся энергия электрона чисто кинетическая E=MV2/2=h2/2?2Mr2, то при её спаде электрон уже не падает на ядро, а отдаляется от него, наращивая r орбиты в атоме неограниченно долго.
Ядро такого атома мы изображали, по концепции Ритца, в виде двух цепочек из чередующихся электронов и позитронов (так же и информационная основа клеточного ядра — двойная цепочка ДНК из чередующихся нуклеотидов). Однако, считается, что электроны и позитроны при контакте исчезают (аннигилируют) с выделением энергии, поскольку после не находят ни электронов, ни позитронов. Но это — лишь иллюзия. Ведь и при взрыве бомбы горючее соединяется с окислителем, резко выделяя энергию. И, хотя здесь тоже в итоге не остаётся ни горючего, ни окислителя, никто не скажет, что они исчезли, обратившись в энергию. Атомы окислителя лишь соединились с атомами горючего, образовав невидимый газ, расширившийся взрывом. Так же, и при контакте позитрона с электроном частицы не исчезают, а, слившись в пару, не имеющую заряда, перестают регистрироваться приборами (§ 1.16). Из таких парных сочетаний электронов и позитронов, судя по всему, и образованы протон, нейтрон и другие "элементарные" частицы, как предполагал ещё Ф. Ленард (§ 3.3), и как позднее обосновал В. Мантуров [79]. Кстати, по квантовой механике электрон и позитрон могли б образовать позитроний, аналогичный атому водорода. Но, на деле, позитроний, в отличие от атомов, нестабилен: кружащиеся частицы сливаются как раз за 10–10 с [82], растратив энергию, чем доказывают порочность планетарной модели, даже в квантовом её варианте. Ведь позитрон, играющий роль ядра, не имеет его структуры и соответствующей конфигурации магнитного поля.
Что же собой представляет ядро атома водорода, иначе говоря, — протон, и как создаётся его структура? Чуть выше, следуя идее Ритца, упрощённо представили ядро в форме крестовины из чередующихся электронов e- и позитронов e+, сравнивая его с кристаллом соли, так же сложенным из периодично размещённых заряженных частиц. Но, поскольку реальные кристаллы, за исключением снежинок, имеют вид многогранников, — параллелепипедов и пирамидок с плоскими гранями, то логичней и проще представлять ядро водорода в виде куба или параллелепипеда, скажем, в виде двойного квадратного слоя частиц (Рис. 101). Именно в виде таких кристаллов правильной формы, как увидим в дальнейшем, логичней всего представлять частицы, в том числе протон, образующий ядро водорода (§ 3.9). Поскольку, как было выяснено выше, масса — это величина аддитивная (§ 1.17), то масса ядра должна равняться сумме масс образующих его электронов и позитронов. Раз протон имеет вес 1836 электронов, то его можно условно изобразить, как параллелепипед с размерами 2х30х30 частиц, или, для точности, 2х27х34=1836. Отметим, что ещё Дж. Томсон, открывший электрон и построивший первую модель атома (см. его книгу "Электричество и материя"), предлагал атом водорода и его массу считать сложенными примерно из тысячи электронов и того же числа положительно заряженных частиц (позитронов) [139].
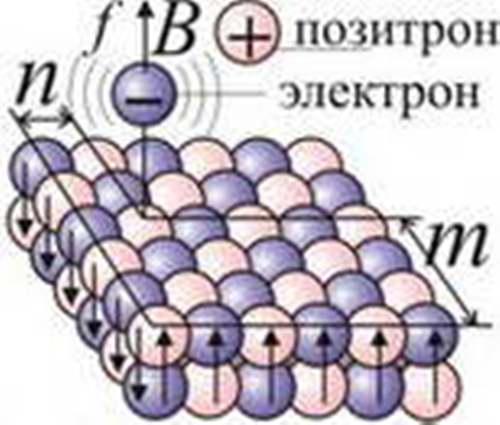
Рис. 101. Возможная структура протона или нейтрона в ядре и схема генерации спектра.
В каждом из слоёв магнитные моменты частиц ориентируются вдоль диагонали слоя, минимизируя энергию взаимодействия. В верхнем и нижнем слое моменты направлены противоположно (Рис. 102.а), образуя структуру магнитного поля, как у крестовины. В этом легко убедиться, представив систему набором магнитных диполей: в эквивалентной схеме (Рис. 101, Рис. 102) только края квадратов создают магнитные поля (они перпендикулярны плоскости слоя и смотрят вверх и вниз). Позитроны e+ и электроны e- расположены в шахматном порядке, подобно ионам Na+ и Cl- в кристалле соли. В атоме водорода электрон прилипает к этой "магнитной шахматной доске", располагаясь точно над позитронами, будучи притянут ими, а при малых колебаниях в магнитном поле ядра он излучает свет. При этом электрон, словно чёрные шашки в игре, дискретно прыгает, шагает по этой шахматной доске, замирая на клетках белого цвета, отвечающих позитронам, отчего дискретно меняется величина магнитного поля и частота колебаний электрона в нём. Поскольку структура магнитного поля получается той же, что и в крестовом атоме, то частота f колебаний и излучения электрона принимает такой же дискретный ряд значений f=Rc(1/n2–1/m2), где n и m — целочисленные координаты узла, в котором сидит электрон (Рис. 101).
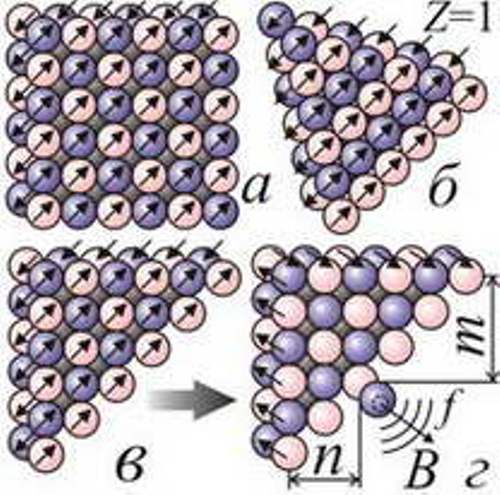
Рис. 102. Строение протонов в форме квадратов и треугольников и ориентация в них магнитных моментов.
Можно представить протон и в виде одинарного квадратного слоя частиц. Складываясь вдоль диагонали пополам, он образует двойной треугольный слой — со структурой поля крестовины и тем же спектром частот. Этот парный треугольник может быть и прямоугольным и равносторонним, тоже дающим водородный спектр (Рис. 102). Кроме водородного, модель позволяет рассчитать и другие атомы. Рассмотрим атом с атомным номером Z — содержащим Z протонов. Квадраты протонов могут, как в сэндвиче, склеиться слоями, если над позитронами одного слоя окажутся электроны другого. Их взаимное притяжение и даёт те ядерные силы, что противостоят отталкиванию протонов и быстро (по экспоненте § 3.12) спадают с удалением [79]. Когда такая "стопка" протонов сложится вдоль диагонали пополам, получится слоёный уголок. В его верхней и нижней части магнитные моменты смотрят в разные стороны вдоль линии сгиба (Рис. 103).
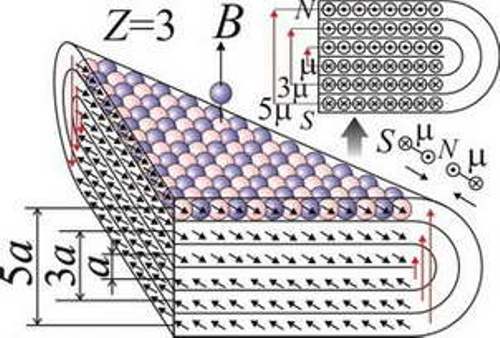
Рис. 103. Склеивание протонов в слоёный уголок с увеличенным в Z2 раз полем B. Выше эквивалентная схема из магнитных диполей ?.
Здесь магнитный момент единицы длины a окажется уже не ?, а ?Z2: он найдётся как сумма магнитных моментов отдельных магнитных диполей, образующих арифметическую прогрессию 1?+ 3?+ 5?+…+(2Z–1)?=?Z2. Соответственно, магнитное поле и частота колебаний в нём электрона вырастет пропорционально Z2: f=RZ2c(1/n2–1/m2). И точно, у ионизованных водородоподобных атомов He+, Li2+, Be3+, B4+, C5+, лишённых всех электронов кроме одного, спектры подчиняются этой формуле, дающей спектр водорода с увеличенным в Z2 раз масштабом. Присутствие остальных электронов привело бы к тому, что своим полем они бы исказили движение электрона, генерирующего спектр, и он приобрёл бы совсем иной характер, чем у водорода (§ 3.4). Впрочем, у многоэлектронных атомов с большим Z магнитное поле столь велико, что вносимые электронами искажения оказываются незначительны. Поэтому, для спектра излучения электронов, крутящихся в столь сильных полях с огромной частотой и генерирующих рентгеновское излучение, справедлив закон Мозли f=R(Z — b)2c(1/n2–1/m2), отличающийся от найденного лишь малой поправкой b, вызванной влиянием остальных электронов [49, 134].
Возможно и другое, более простое объяснение изменению постоянной Ридберга R с изменением атомного номера и заряда ядра Z. Возможно, пропорционально росту заряда ядра Z уменьшается равновесное расстояние a=a0/Z между электронами и позитронами и, соответственно, увеличивается R=h/16?2ca2M=RHZ2. Это было бы возможно, если б это равновесное расстояние задавалось, например, амплитудой колебаний электронов возле ядра, или если б оно задавалось магнитным моментом и зарядом ядра (в сумме с моментом и зарядом окружающих его электронов внутренних оболочек), так же, как расстояние между магнитными поплавками в опытах А. Майера определялось магнитным моментом центрального магнита (ядра атома § 3.1). Такое изменение равновесного расстояния между электронами в электронных оболочках позволило бы также объяснить уменьшение размеров атомов при росте атомного номера в периодах таблицы Менделеева.
В магнитном поле атома электроны могут совершать два типа "колебаний". Одни электроны кружатся с жёстко заданными частотами возле узлов атома, генерируя дискретный спектр излучения. Такие электроны будем называть "внутренними", или "узловыми". Другие же, словно в магнитной ловушке, кружатся с непрерывно меняющейся частотой f вокруг самого атома, обладая энергией E=hf. Эти электроны, которые назовём "внешними", или "орбитальными", создают сплошной (тепловой) спектр излучения и не занимают в атоме устойчивых положений, а кружатся в магнитном поле атомного остова (Рис. 107). Это внешнее магнитное поле уже не зависит от порядкового номера элемента и одинаково для всех атомов. Внешние электроны, пойманные в магнитную ловушку атома, порождают также фотоэффект и Комптон-эффект (§ 4.3, § 4.7). Такие электроны не задерживаются в атоме надолго, а регулярно, — от потерь энергии и схода с орбиты, покидают его и захватываются новыми атомами. В целом, атом — это своего рода комбинация разных приборов: магнитной ловушки, рупорной антенны, гиротрона, циклотрона, — преобразующих движение электронов в излучение и обратно. Так что, в атоме действуют обычные законы механики, вакуумной СВЧ-электроники и — совершенно нет квантовых, как отмечал ещё К.Э. Циолковский, тоже создавший чисто классическую модель атома, о которой, правда, ныне ничего не известно. Известно лишь, что с этой моделью, описанной в работе Циолковского "Гипотеза Бора и строение атома" был, вероятно, ознакомлен через А.Б. Шершевского А. Эйнштейн [69, с. 185]. Но это уже совершенно забытая история.
Выходит, Циолковский был прав: классическими законами вполне можно объяснить спектры атомов, если использовать кристаллическую магнитную модель атома Ритца. Более того, спектры буквально кричат именно о такой чёткой модели. Идеально похожие для атомов одного элемента наборы спектральных линий с частотами, заданными точными соотношениями с целочисленными переменными, — разве это не удивительно? Столь чёткая структура линий может возникать лишь в кристаллоподобном атоме, где электроны, генерирующие спектр, занимают лишь некоторые устойчивые положения, отделённые одно от другого шагом дискретизации, равным периоду кристаллической электрон-позитронной решётки. Именно Вальтер Ритц, первым нашедший общую формулу для атомных спектров, показал, что атомный механизм генерации спектра обусловлен периодичным расположением частиц. Итак, дискретные атомные спектры подтверждают дискретную кристаллическую структуру атома.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
СОВЕТСКИЕ АТОМНЫЕ ШПИОНЫ В ВЕЛИКОБРИТАНИИ
СОВЕТСКИЕ АТОМНЫЕ ШПИОНЫ В ВЕЛИКОБРИТАНИИ Имена всех «тайных информаторов Москвы» мы никогда не узнаем. Ниже мы расскажем только о тех, чьи имена попали в «открытую» печать и чей факт сотрудничества с советской разведкой был подтвержден официально.Австрийский физик
9.8. Обратный ход модели
9.8. Обратный ход модели Фаза исследования только что созданной теории включает деятельность по двум направлениям. Первое — это всесторонняя проверка теории, сравнение ее с опытом, поиск изъянов. Но допустим, теория хороша. Тогда на первый план выступает второе
Другие модели
Другие модели Полученный при конструировании системы телеслежения опыт поможет читателю в создании других моделей. Компания, производящая Erector Sets, постоянно совершенствует и обновляет ассортимент интересных конструкторских наборов, выпускаемых на рынок. Эти наборы,
Соленые спектры
Соленые спектры Когда электрон изменяет скорость или направление движения, он испускает электромагнитное излучение. В таком случае, считает Дедал, при прохождении электрического тока по извилистому проводнику должен излучаться свет. Частота излучаемого «света» в
Глава 19 Атомные атакующие подлодки
Глава 19 Атомные атакующие подлодки В этой главе• 62 подлодки класса «Лос-Анджелес».• Значение стали HY-100.• Класс «Вирджиния» — подлодки будущего.• Последние достижения в видео — и аудиооборудовании.• Глубоководные подлодки и морское дно.Вы уже знаете достаточно
20.9. Вычисления с использованием атомов
20.9. Вычисления с использованием атомов А теперь поговорим о возможностях создания сверхминиатюрной вычислительной техники. Со времен лекции 1959 года эта область стремительно развивалась, так что возникла совершенно новая ситуация, и я буду обсуждать только новейшие
§ 3.3 Строение атомов и периодический закон Менделеева
§ 3.3 Строение атомов и периодический закон Менделеева Свойства простых тел, а также формы и свойства соединений элементов, находятся в периодической зависимости (или, выражаясь алгебраически, образуют периодическую функцию) от их атомных весов. Д.И. Менделеев Считается,
§ 3.7 Ядерные спектры и эффект Мёссбауэра
§ 3.7 Ядерные спектры и эффект Мёссбауэра При максимально возможной опоре на механику или электродинамику необходимо указать физически наглядные математические операции, интерпретация которых через колебания подходящей модели приводит для неё к законам сериальных
Модели и самолеты
Модели и самолеты Продолжение, начало в ИА №1/20012-й ВЫПУСК: «В цветах “Интерфлюга” и “Аэрофлота”» (1963 – 1969 г.г.) «Каравелла»3 авиакомпании «Эр Франс» в московском аэропорту Домодедово (фото из архива Г.Петрова).Формальным поводом для качественной переработки продукции,
4. Современные модели СВЧ-печей
4. Современные модели СВЧ-печей В этой главе рассмотрены современные модели СВЧ-печей и дан краткий сравнительный анализ по классу этих установок. При сравнении характеристик и режимов различных бытовых СВЧ-устано-вок следует иметь в виду, что указанные режимы
PLASTICART модели и самолеты
PLASTICART модели и самолеты Продолжение, начало в ИА № 1–5/2001.4-й ВЫПУСК: СМЕНА ПРИОРИТЕТОВ (1977–1986 ГГ.)(продолжение) Модели Ту-2 и Бе-6 хотя и были вполне подходящим пополнением многих коллекций, всё же несли в себе значительное количество ошибок. Впрочем, многие из них были
Погрешности: модели
Погрешности: модели Когда мы что-то измеряем, имеющуюся к моменту начала измерений информацию (как осознанная, так и неосознанная) удобно представить в виде моделей объекта или явления. Модель «нулевого уровня» — это модель наличия величины. Мы верим в то, что она есть —