9.7. Арифметика с птичьего полета

9.7. Арифметика с птичьего полета

Ситуации и представления в нервной системе человека моделируют смену состояний окружающей среды. Языковые объекты моделируют смену ситуаций и представлений. В результате теория является «двухэтажной» языковой моделью действительности (рис. 9.5). Схема использования теории такова. Ситуация S_i кодируется языковым объектом L_i. Этот объект, конечно, может состоять из множества других объектов и иметь сколь угодно сложную структуру. Объект L₁ есть имя для S₁. Некоторое время спустя ситуация S₁ сменяется ситуацией S₂. Осуществляя некоторую языковую деятельность, мы преобразуем L₁ в другой объект L₂, и, если наша модель правильна, L₂ есть имя S₂. Тогда, не зная реальной ситуации S₂, мы можем получить о ней представление путем декодирования языкового объекта L₂. Языковая модель определяется, очевидно, как семантикой объектов L_i («материальная часть» по военной терминологии), так и видом языковой деятельности, превращающей L₁ в L₂.

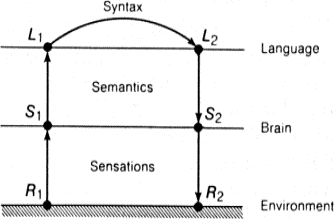
Рис. 9.5. Двухэтажная языковая модель действительности

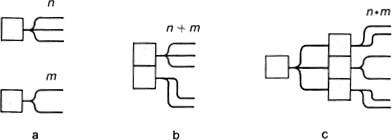
Рис. 9.6. Действия над целыми числами

Заметьте, что мы ничего не сказали о «выделении существенных сторон явления», о «причинно-следственной связи» и прочих подобных вещах, которые обычно красуются на почетных местах при описании сущности научного моделирования. И ситуация S₁ у нас «не порождает» ситуацию S₂, а лишь «сменяется» ею. Это, конечно, не случайно. Нарисованная нами схема логически предшествует упомянутым философским понятиям. Если у нас есть языковая модель, и лишь постольку, поскольку она у нас есть, мы можем говорить о существенных сторонах явления, об идеализации, о причинно-следственной связи и т. п. Все эти понятия, хотя они по внешности предстают как условия создания языковой модели, на самом деле являются лишь описанием в общих терминах (конечно, очень важным и нужным) уже существующих моделей. Хотя эти понятия как-будто бы «объясняют», почему вообще может существовать языковая модель, на самом деле они сами являются элементами языковой модели следующего уровня (иерархии по управлению) и исторически, конечно, появляются позже, чем первичные языковые модели (например, арифметические). Поэтому, прежде чем использовать эти понятия, мы должны констатировать, что языковые модели вообще существуют. И на этом уровне описания нам нечего добавить к схеме на рис. 9.5. «Так бывает» — вот и все.

Как же создаются и развиваются теории? Как и все в мире, по методу проб и ошибок. Если есть отправная точка, то, начиная от нее, человек принимается сооружать языковые конструкции и исследовать, что у него получилось. Фазы конструирования и исследования постоянно сменяют друг друга: конструкция порождает исследование, исследование порождает новые конструкции.

Отправной точкой арифметики является понятие числа (целого). Аспект действительности, который отражает это понятие таков: отношение целого к его частям, способ разложения целого на части. Ту же самую мысль можно выразить и с противоположной стороны: число — способ объединения частей в целое, т. е. в некое множество (конечное). Два числа считаются тождественными, если части (элементы множества) можно поставить во взаимно однозначное соответствие; в установлении этого соответствия и состоит счет. Очевидно, однако, что одних чисел мало для теории, необходимы еще действия над ними — элементы функционирования модели, преобразования L₁ ? L₂. Возьмем два числа n и m и представим их схематически как два способа разложения целого на части (рис. 9.6,a).

Как из этих двух чисел получить третье, т. е. третий способ разложения целого на части? Сразу приходит на ум два способа, которые можно назвать параллельным и последовательным соединением разложений. При параллельном способе оба целых образуют в качестве частей новое целое (рис. 9.6,b). Это разложение (число) мы назовем суммой двух чисел. При последовательном способе мы берем одно из разложений и каждую его часть разлагаем в соответствии с другим разложением (рис. 9.6,c). Новое число называется произведением. Оно не зависит от порядка производящих чисел. Это очень хорошо видно, если интерпретировать действия над числами не как соединение разложений, а как образование нового множества. Сумма есть, очевидно, результат слияния двух множеств в одно (объединение множеств). Произведение имеет своим прообразом множество сочетаний любого элемента первого множества с любым элементом второго (такое множество называется в математике прямым произведением множеств). Связь этого определения с предыдущим можно проследить таким образом. Пусть первое разложение делит целое A на части a₁, a₂, ..., a_n, второе делит B на части b₁, b₂, …, b_m. Сделав первое разложение, пометим буквами a_i полученные части. Разлагая каждую часть второго на части b_i сохраним первую букву и добавим вторую. Значит, на каждой части результата будет стоять a_ib_j и все эти сочетания будут разные. Подходы от целого к части и от части к целому дополняют друг друга. Из рис. 9.6,c легко увидеть также, что умножение можно свести к повторному сложению.

Конечно, древний человек, создавая арифметику, был далек от этих рассуждений. Но ведь и лягушка не знала, что ее нервная система должна быть устроена по иерархическому принципу! Важно, что это знаем мы.

Имея языковые объекты, изображающие числа, и умея производить над ними сложение и умножение, мы уже получаем теорию, дающую нам работающие модели действительности. Разберем простейший пример, поясняющий схему на рис. 9.5.

Пусть некий земледелец засеял пшеницей поле длиной в 60 шагов и шириной 25 шагов. Допустим, что он ожидает урожая в одну кружку пшеницы с квадратного шага. Прежде чем приступать к уборке, он хочет знать, сколько он получит кружек пшеницы. Здесь S₁ — ситуация перед уборкой пшеницы, включающая, в частности, результат измерения длины и ширины поля в шагах и ожидаемую урожайность; S₂ — ситуация после уборки, включающая, в частности, результат измерения количества пшеницы кружками; L₁ — языковый объект 60 ?25 (знак умножения является таким же отражением ситуации S₁, как числа 60 и 25: он отражает структуру множества квадратных шагов на плоскости как прямого произведения множеств линейных шагов в длину и ширину); L₂ — языковый объект 1500.

Терминологическое замечание. Под теорией мы понимаем просто языковую модель действительности, дающую нечто новое по сравнению с нейронными моделями. В этом определении не учитывается, что теории могут образовывать иерархию по управлению, да этот факт и трудно отразить без введения математического аппарата. Более общие модели могут порождать более частные модели. Теорию и языковую модель мы будем считать синонимами, но все же, когда речь идет о порождении одной модели другой моделью, мы более общую будем называть теорией, а более частную — моделью.