Глава 10. От Фалеса до Евклида

Глава 10. От Фалеса до Евклида

10.1. Доказательство

Ни в египетских, ни в вавилонских текстах мы не находим ничего, что хотя бы отдаленно было похоже на математическое доказательство. Понятие о доказательстве ввели греки, и это является их величайшей заслугой. Какими-то наводящими соображениями при получении новой формулы люди, очевидно, пользовались и раньше, мы даже приводили пример грубо неверной формулы (для площади неправильных четырехугольников у египтян), явно полученной из внешне правдоподобных «общих соображений». Но только греки стали относиться к этим наводящим соображениям с той серьезностью, которой они заслуживают, стали анализировать эти соображения с точки зрения их убедительности и ввели принцип, согласно которому каждое утверждение, касающееся чисел и фигур (формула), за исключением лишь небольшого числа, должно быть доказано, выведено убедительным, не допускающим сомнений образом из этих «совершенно очевидных» истин. Неудивительно, что именно греки с их демократическим общественным строем создали учение о математическом доказательстве. Споры и доказательство играли важнейшую роль в жизни граждан греческого города-государства (полиса). Понятие о доказательстве уже существовало, оно было общественно значимой реальностью. Осталось только перенести его в область математики, что и было сделано, едва греки познакомились с достижениями древних восточных цивилизаций. Сыграло здесь роль, надо полагать, и то положение молодого любознательного ученика, в котором оказались греки по отношению к египтянам и вавилонянам — своим старшим и не всегда согласным друг с другом учителям. В самом деле, вавилоняне определяют площадь круга по формуле 3r², а египтяне по формуле (⁸/₉ 2r)² . Где же истина? Здесь есть о чем подумать и поспорить.

Творцы египетской и вавилонской математики остались безымянными. Греки сохранили имена своих мудрецов. Первое из них — имя Фалеса Милетского — является также первым именем, вошедшим в историю науки. Фалес жил в VI в. до н. э. в городе Милете на Малоазиатском побережье Эгейского моря. Одна дата из его жизни установлена твердо: в 585 г. до н. э. он предсказал солнечное затмение. Этот факт, кстати, неоспоримо свидетельствует о знакомстве Фалеса с культурой древних цивилизаций, ибо, чтобы установить периодичность затмений, необходим опыт десятков и сотен лет. Так как у Фалеса не было греческих предшественников, он мог заимствовать свои познания по астрономии только у ученых Востока.

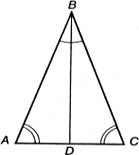
Рис. 10.1. Равнобедренный треугольник

Фалес, как утверждают греки, дал миру первые математические доказательства. В числе доказанных им положений (теорем) называют следующие:

Диаметр делит круг на две равные части.

Углы при основании равнобедренного треугольника равны.

Два треугольника, у которых одинаковы стороны и прилежащие к ней углы, равны.

Кроме того, он первый дал построение круга, описанного вокруг прямоугольного треугольника (и в честь этого открытия, как говорят, принес в жертву быка).

Простейший характер указанных теорем, их интуитивная очевидность показывают, что Фалес полностью осознавал значение доказательства как такового. Эти теоремы, явно доказывались не потому, что были сомнения в их истинности, а с целью положить начало систематическому нахождению доказательств, разработать технику доказательства. Имея такую цель, естественно начинать с доказательства самых простых предложений.

Пусть треугольник ABC равнобедренный (рис. 10.1), т. е. сторона AB равна стороне BC. Разделим угол ABC линией BD на две равные части. Перегнем мысленно наш чертеж по линии BD. Так как угол ABD равен CBD, линия BA ляжет на линию BC, а так как длины отрезков AB и BC равны, точка A ляжет на точку C. Поскольку точка D остается на месте, углы BCD и BAD должны быть равны. Если раньше нам только казалось, что углы BCD и BAD одинаковы (так, вероятно, говорил своим согражданам Фалес), то теперь мы доказали, что эти углы необходимо и с абсолютной точностью должны быть равны (тогда говорили «подобны») друг другу, т. е. совмещаться при наложении.

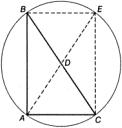
Рис. 10.2. Построение окружности, описанной вокруг прямоугольного треугольника