3.8. Моделирование

3.8. Моделирование

До сих пор, говоря об ассоциациях представлений, мы полностью игнорировали их динамический, временной аспект, т. е. рассматривали связываемые представления как статические и не имеющие никакой координаты во времени. Между тем идея времени может активно входить в наши представления. Мы можем представить себе фигуры, движущиеся и меняющиеся с определенной скоростью, можем мысленно продолжить наблюдаемый процесс. По дороге катится колесо. Вы закрываете глаза на пару секунд и представляете движение колеса. Открыв глаза, вы видите его на том самом месте, где и ожидали. Это, конечно, результат ассоциации представлений, но такой ассоциации или, вернее, таких представлений, которые органически связаны с течением времени. Положение x колеса в момент времени t ассоциируется с положением х₁ в момент времени t + ?t, а также с положением х₂ в момент времени t + 2?t и т. д. Каждое из этих представлений включает в себя представление о времени, к которому оно относится. Каков механизм этого включения, мы не знаем и в соответствии с нашим подходом не будем строить на этот счет никаких гипотез. Заметим только, что ничего особенно удивительного в таком включении нет. Хорошо известно, что в организме есть свой датчик времени — «внутренние часы».

Ассоциация представлений, имеющих временную координату, дает вам возможность предвидеть в своем воображении будущие ситуации. Мы установили наличие таких представлений, опираясь на внутренний, субъективный опыт. Но из того факта, что животные также обнаруживают способность предвидения (посмотрите, как ловит собака кусок сахара), мы заключаем, что их представления могут обладать временной координатой.

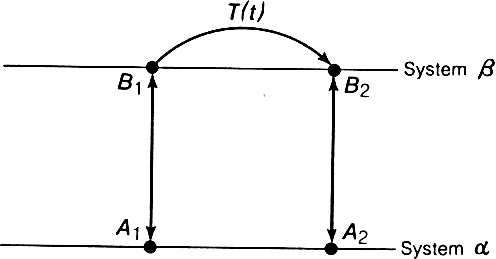
Рис. 3.8. Схема моделирования

Говоря языком кибернетики, связывание представлений, включающих временную координату, и вытекающая отсюда способность предвидеть будущее есть не что иное, как моделирование, построение модели окружающей среды.

Дадим общее понятие модели. Рассмотрим две системы ? и ?. Допустим, что каждому состоянию A_i, системы ? мы можем каким-то образом сопоставить одно определенное состояние B_i, системы ? (рис. 3.8).

Обратное соответствие не обязательно должно быть однозначным, т. е. одному состоянию ? может соответствовать множество состояний ?. Так как обобщенное состояние согласно нашему определению есть множество состояний, можно характеризовать это положение как взаимно однозначное соответствие состоянии системы ? обобщенным состояниям системы ?. Это необходимо, но не достаточно, чтобы считать систему ? моделью системы ?. Должно еще существовать такое преобразование T(t) системы ?, зависящее от времени t, которое моделирует естественное течение времени в системе ?. Это означает следующее. Пусть первоначально система ? находится в обобщенном состоянии A₁, которому соответствует состояние B_i, системы ?. Пусть по прошествии времени t состояние системы ? становится A₂. Тогда преобразование T(t) должно переводить систему ? в состояние B₂, соответствующее обобщенному состоянию A₂. Если это условие выполнено, мы называем систему ? моделью системы ?.

Преобразование T(t) может, в частности, заключаться просто в том, что мы предоставляем системе ? самой по себе менять свое состояние со временем. Такие модели называют моделями в естественном масштабе времени.

...Осаждающие сделали подкоп под крепостную стену и заложили в него несколько бочек с порохом. Рядом горит свеча, от основания которой начинается пороховая дорожка к бочкам. Когда свеча догорит, будет взрыв. Точно такая же свеча, зажженная в то же время, горит на столе в палатке предводителя осаждающих. Эта свеча служит для него моделью первой. Зная, сколько времени осталось до взрыва, он отдает последние распоряжения... Свирепые лица склонились над столом, волосатые руки сжимают оружие. Свеча догорает. Страшный взрыв сотрясает воздух. Модель не подвела...

Изображение на экране телевизора, когда идет трансляция футбольного матча, можно тоже формально считать моделью футбольного поля и трибун стадиона. Действительно, все условия соблюдены. Однако чувствуется большое различие между случаем двух свечей и случаем трансляции матча. В чем оно состоит? В различии информационных связей между системами ? и ?. Любое изображение ? объекта ? является в широком смысле слова его моделью. Но от ? к ? существует непрерывный поток информации, и только благодаря этому потоку сохраняется соответствие между состояниями ? и ?. Имея информационный доступ к ?, мы фактически имеем доступ к ?. Система ? служит лишь фазой передачи информации от ?. Совсем другое дело в случае двух свечей. Свеча ? горит с такой же скоростью, как свеча ?, но независимо от нее. Предводитель осаждающих не имеет доступа к свече ? и не может получить никакой реальной информации о ее состоянии. Путем моделирования он компенсирует этот недостаток получением эквивалентной информации. Система ? играет здесь принципиально другую, более существенную роль. С ее помощью как бы преодолевается пространственный барьер, причем без установления каких-либо новых информационных каналов.

Еще более важен случай, когда модель помогает преодолевать не пространственный, а временной барьер. Информационного канала в будущее, увы, не проложишь. А модель позволяет нам действовать так, как будто такой канал есть. Для этого надо только, чтобы выполнение преобразования T(t) над моделью занимало меньше времени, чем само время t. Можно было бы привести много примеров использования таких моделей в жизни современного человека, однако вряд ли в этом есть необходимость. Вернемся еще раз к ассоциациям представлений.

Мы видели, что ассоциации статических представлений отражают наличие пространственных корреляций, взаимосвязей в окружающей среде. Точно так же ассоциации динамических представлений — модели, создаваемые мозгом — отражают динамические временные корреляции, свойственные внешней среде. Ситуация х через время t вызывает (или может вызвать) ситуацию Y — вот общая формула таких корреляций, и эти корреляции запечатлеваются в мозгу в виде соответствующих ассоциаций.