А. Круговая скорость
Как найти величину круговой скорости, то есть той скорости, с которой должен двигаться спутник, чтобы его высота над Землей оставалась неизменной?
Высота спутника не меняется в том случае если он каждое мгновение на столько же удаляется от Земли в своем движении по инерции, на сколько приближается к ней в результате непрекращающегося падения на Землю. Это и позволяет найти необходимую круговую скорость спутника.
Рассмотрим движение спутника за 1 секунду, причем для простоты будем считать, что спутник движется у самой поверхности Земли, то есть высота равна нулю. Тогда за 1 секунду спутник приблизится к центру Земли, в результате притяжения к ней, на величину
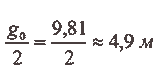
На эту же величину он должен удалиться от центра Земли, что позволяет построить прямоугольный треугольник (см. рисунок).
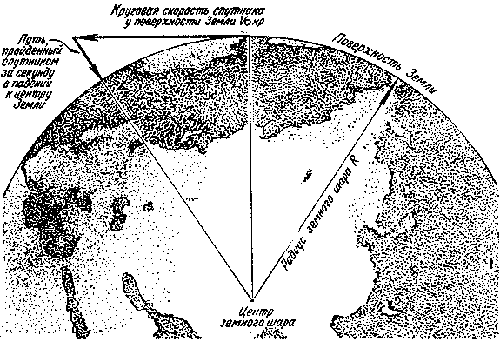
Так можно определить круговую скорость искусственного спутника Земли (масштаб построения не соблюден).
По теореме Пифагора
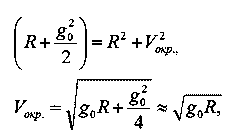
Vокp. = ?9,81·6 378 000 = 7910 м/сек.
Эту же задачу можно решить и иначе. Если высота спутника не меняется, то это значит, что его центростремительное ускорение в точности равно ускорению земного тяготения. (Это вовсе не означает, как иногда пишут, что центробежная сила «уравновешивает» вес спутника.)
Следовательно,
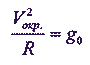
и
Vокp= ?g0R,
как и ранее.
Как изменяется круговая скорость с высотой орбиты спутника?
Очевидно; на высоте Н
Vкp = ?g(R+H)
Но так как то
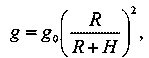
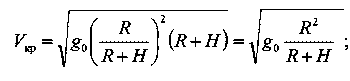
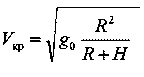
Это значит, что круговая скорость изменяется обратно пропорционально корню квадратному из расстояния до центра Земли.
Высота Н в км Круговая скорость Vкр. в м/сек 0 7 910 255 7 760 1 000 7 360 1 670 7 040 35 800 3 080 384 000 (орбита Луны) 1 010Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК