VII. ФОРМА ЭЛЛИПТИЧЕСКОЙ ОРБИТЫ
Для определения эллиптической орбиты, помимо величины большой полуоси, необходимо знать еще один из элементов орбиты — малую полуось b, полуфокусное расстояние с или эксцентриситет е. Эти величины связаны следующими соотношениями:
полуфокусное расстояние
с = ?a2 — b2
эксцентриситет

Для искусственных спутников Земли очевидны также следующие соотношения:
средняя высота спутника над Землей
Hср = a — 6378 км,
или где Hап. — высота апогея орбиты;

Hпер.— высота перигея орбиты;
полуфокусное расстояние орбиты

Примеры использования формул
1. Определить элементы орбит советских искусственных спутников Земли по известным высотам апогея и перигея.
В соответствии с опубликованными данными примем следующие округленные значения для высот апогея и перигея советских искусственных спутников Земли:
Hпер. = 225 км (для всех трех спутников);[146]
Hап.1 = 950 км, Hап.2 = 1670 км, Hап.3 = 1880 км.
Тогда средние высоты спутников над Землей будут равны:
для первого спутника Hср1 =

для второго спутника Hср2 =

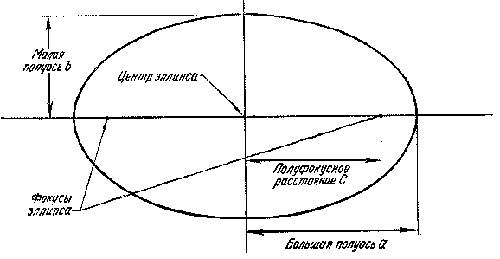
Элементы эллиптической орбиты.
для третьего спутника Hср3 =

а полуфокусные расстояния соответственно:

Теперь можно определить величины больших и малых осей орбит:
a1= Hср1+6378 = 588 + 6378 = 6966 км,
а2 = 948 + 6378 = 7326 км,
а3 = 1053 + 6378 = 7431 км,

2. На сколько орбиты советских искусственных спутников Земли отличаются от круга?
Эксцентриситет орбит советских спутников весьма мал, то есть эллиптические орбиты спутников весьма мало отличаются от круга:

Действительно, разность полуосей орбит равна:
а1 — b1 = 6966–6955 = 11 км,
а2 — b2 = 7326–7290 = 36 км,
а3 — b3 = 7431–7385 = 46 км,
В масштабе чертежа, на котором схематически изображены орбиты советских спутников, эта разность неощутима, и орбиты практически становятся кругами.

Схематическое изображение орбит первых советских искусственных спутников Земли.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК