Альберт Эйнштейн, Людвиг Инфельд Эволюция физики: развитие идей от первоначальных понятий до теории относительности и квантов

Время, пространство, относительность.

Наши новые положения суть:

1. Скорость света в вакууме одинакова во всех системах координат, движущихся прямолинейно и равномерно друг относительно друга.

2. Законы природы одинаковы во всех системах координат, движущихся прямолинейно и равномерно друг относительно друга.

Теория относительности начинается с этих двух положений. С этого времени мы не будем применять классического преобразования, так как знаем, что оно противоречит исходным положениям.

В данном случае, как и всегда в науке, важно отказаться от глубоко укоренившихся, часто некритически повторяемых предрассудков. Так как мы видели, что изменения обоих положений приводят к противоречию с экспериментом, то мы должны иметь смелость твердо установить их справедливость и напасть на один возможно слабый пункт, а именно на способ, которым координаты и скорости преобразуются от одной системы координат к другой. Мы хотим сделать выводы их этих двух положений, посмотреть, где и как эти положения противоречат классическому преобразованию, и найти физический смысл полученных результатов.

Можно еще раз использовать пример с движущейся комнатой и наблюдателями внутри и вне ее. Пусть световой сигнал опять излучается из центра комнаты, и вновь мы спрашиваем обоих людей, что они обнаружат, допустив только два вышеуказанных принципа и забыв то, что было предварительно сказано о среде, сквозь которую проходит свет. Приведем их ответ.

Внутренний наблюдатель. Световой сигнал, идущий от центра комнаты, достигнет стен одновременно, так как все стены одинаково отстоят от источника света, а скорость света одинакова во всех направлениях.

Внешний наблюдатель. В моей системе координат скорость света совершенного такая же, как и в системе наблюдателя, движущегося вместе с комнатой. Мне нет дела до того, движется ли источник света в моей системе или нет, так как его движение не влияет на скорость света. То, что я вижу, это — световой сигнал, идущий с постоянной скоростью, одинаковой во всех направлениях. Одна из стен стремится убежать от светового сигнала, а другая — приблизиться к нему. Поэтому убегающая стена будет достигнута световым сигналом немного позднее, чем приближающаяся. Хотя эта разность времен прибытия светового сигнала будет очень незначительной, если скорость комнаты мала сравнительно со скоростью света, тем не менее световой сигнал не достигнет обеих противоположных стен, расположенных перпендикулярно к направлению движения, совершенно одновременно.

Сравнивая предсказания обоих наблюдателей, мы обнаруживаем крайне изумительный результат, который явно противоречит несомненно хорошо обоснованным понятиям классической физики. Оба события — достижение стен двумя световыми лучами — одновременны для наблюдателя внутри и неодновременны для наблюдателя вне комнаты. В классической физике у нас были одни часы, одно течение времени для всех наблюдателей во всех системах. Время, а стало быть, и такие слова, как «одновременно», «ранее», «позднее», имели абсолютное значение, независимое от какой-либо системы. Два события, происходящие в одно и то же время в одной системе координат, необходимо происходили одновременно во всех системах координат.

Положения, указанные выше, т. е. теория относительности, вынуждают нас отказаться от этого взгляда. Мы описали два события, которые происходят одновременно в одной системе координат, но в разное время в другой системе. Наша задача — понять это следствие, понять смысл предложения: «Два события, одновременные в одной системе координат, не могут быть одновременны в другой системе».

Что мы обозначаем словами: «два одновременных события в одной системе координат»? Интуитивно каждый человек считает, что он понимает смысл этого предложения. Но будем осторожными и постараемся дать строгие определения, так как мы знаем, как опасно переоценивать интуицию. Ответим сначала на простой вопрос.

Что такое часы?

Примитивное субъективное чувство течения времени позволяет нам упорядочить наши впечатления, судить о том, что одно событие происходит раньше, другое позднее. Но чтобы показать, что промежуток времени между двумя событиями равен десяти секундам, нужны часы. Благодаря применению часов понятие времени становится объективным. В качестве часов может быть использовано любое физическое явление, если только оно может быть повторено столько раз, сколько необходимо. Если мы возьмем интервал между началом и концом такого события за единицу времени, то любые интервалы времени мы можем измерить повторением этого физического процесса. Все часы, от простых песочных до наиболее совершенных, основаны на этой идее. При пользовании песочными часами единицей времени будет являться интервал, в течение которого песок высыпается из верхнего стаканчика в нижний. Тот же физический процесс может быть повторен перевертыванием стакана.

Пусть в двух отдаленных друг от друга точках пространства находится двое идеально идущих часов, точно показывающих одинаковое время. Это положение будет справедливым, несмотря на ту осторожность, с которой мы его проверяем. Но что это в действительности означает? Как можем мы удостовериться, что отдаленные друг от друга часы всегда показывают одинаковое время? Можно использовать один из возможных методов — телевидение. Легко понять, что телевидение берется как пример, само по себе оно не существенно для наших доводов. Я мог бы стоять около одних часов и смотреть на изображение других часов на экране телевизора. Тогда я мог бы судить, показывают ли часы одновременно одинаковое время или нет. Но это не было бы хорошим доказательством. Изображение в телевизоре передается электромагнитными волнами, следовательно, распространяется со скоростью света. На экране телевизора я вижу изображение, посланное некоторое очень короткое время тому назад, в то время как на часах, стоящих возле меня, я вижу то, что имеет место в настоящий момент. Эту трудность можно легко преодолеть. Для этого нужно рассмотреть изображения обоих часов в точке, одинаково отстоящей от каждых из них, т. е. рассмотреть их в точке, лежащей на середине расстояния между часами. Тогда, если сигналы посланы одновременно, они достигнут меня в один и тот же момент. Если двое хороших часов, наблюдаемых в точке, находящейся посредине между нами, показывают одинаковое время, то они вполне подходят для указания времени событий в двух отдаленных точках.

В механике мы употребляли только одни часы. Но это было не очень удобно, потому что мы должны были производить все измерения вблизи этих часов. Смотря на удаленные от нас часы, например, с помощью телевизора, мы всегда должны помнить следующее: то, что мы видим теперь, в действительности произошло раньше, подобно тому, как, рассматривая заход Солнца, мы отмечаем это событие спустя восемь минут после того, как оно имело место. Во все показания часов мы должны вносить поправки, соответствующие нашему расстоянию от часов.

Поэтому неудобно иметь только одни часы. Однако теперь, поскольку мы знаем, как проверить, показывают ли двое или вообще несколько часов одновременно одно и то же время, и идя тем же самым путем, мы легко можем вообразить себе в данной системе координат столько часов, сколько нам хочется.

Каждые из них помогут нам определить время событий, происходящих в непосредственном соседстве с ними. Все часы находятся в покое относительно системы координат. Они являются «хорошими» часами; они синхронизированы, что означает, что часы одновременно показывают одинаковое время.

В нашей расстановке часов нет ничего удивительного или странного. Вместо одних-единственных часов мы применяем теперь много синхронизированных часов и поэтому можем легко проверить, одновременны ли два отдаленных события в данной системе координат или нет. Они одновременны, если синхронизированные часы вблизи них показывают одинаковое время в момент, когда происходят события. Теперь утверждение, что одно отдаленное событие происходит раньше другого, имеет определенный смысл. Его можно проверить с помощью синхронизированных часов, покоящихся в нашей системе координат.

Все это находится в согласии с классической физикой и не вызывает еще противоречий с классическим преобразованием.

Для определения одновременности событий часы синхронизируются с помощью сигналов. В наших рассуждениях существенно то, что сигналы передаются со скоростью света, со скоростью, которая играет такую фундаментальную роль в теории относительности.

Так как мы хотим заняться важной проблемой о двух системах координат, движущихся прямолинейно и равномерно относительно друг друга, то мы должны рассмотреть два стержня, снабженных часами. В каждой из обеих систем, движущихся друг относительно друга, наблюдатель имеет теперь свой собственный масштаб со своим собственным набором часов, жестко связанным с масштабом.

При измерениях в классической механике мы употребляли одни часы во всех системах координат. Теперь мы имеем много часов в каждой системе координат. Это различие несущественно. Одни часы были достаточны, но никто не может возражать против употребления многих часов, пока они ведут себя как хорошо синхронизированные часы.

Теперь мы приближаемся к существенному пункту, показывающему, где классическое преобразование противоречит теории относительности. Что происходит, когда двое часов движутся прямолинейно и равномерно друг относительно друга? Физик, держащийся классических взглядов, ответил бы: ничего; их ритм остается одинаковым, и мы можем употреблять для показания времени движущиеся часы так же, как и покоящиеся. Таким образом, согласно классической физике два события, одновременные в одной системе координат, будут одновременными в любой другой системе.

Но это не единственный возможный ответ. Мы можем столь же легко представить себе движущиеся часы, имеющие ритм, отличный от ритма покоящихся часов. Обсудим теперь эту возможность, не решая пока вопроса о том, изменяют ли на самом деле часы свой ритм при движении или нет. Что означает утверждение, что движущиеся часы изменяют свой ритм? Предположим ради простоты, что в верхней системе координат у нас только одни часы, а в нижней — много. У всех часов одинаковый механизм и нижние часы синхронизированы, т. е. они показывают одновременно одинаковое время. Мы показали (рис. 56)[210] три последовательных положения обеих систем, движущихся друг относительно друга.

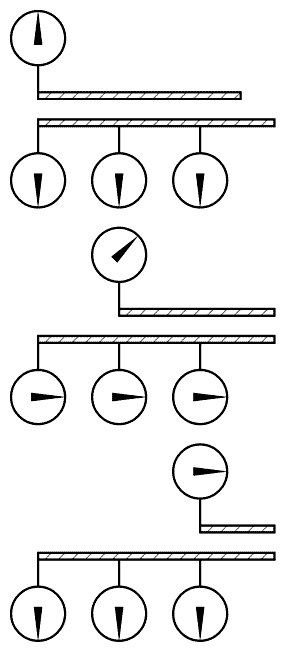
Рис. 56.

На первом рисунке положения стрелок верхних и нижних часов ради удобства взяты одинаковыми; так мы их поставили сами. Все часы показывают одинаковое время. На втором рисунке мы видим относительные положения обеих систем спустя некоторое время. Все часы в нижней системе показывают одинаковое время, но часы в верхней системе вышли из общего ритма. Их ритм изменился, и время отличается вследствие того, что часы движутся относительно нижней системы. На третьем рисунке мы видим, что различие в положении стрелок со временем увеличилось. Наблюдатель, покоящийся в нижней системе координат, нашел бы, что движущиеся часы изменили свой ритм. Конечно, тот же результат получился бы, если бы часы двигались по отношению к наблюдателю, покоящемуся в верхней системе координат; в этом случае в верхней системе должно было бы быть много часов, а в нижней только одни. Закон природы должен быть одинаков в обеих системах, движущихся друг относительно друга.

В классической механике молчаливо предполагалось, что движущиеся часы не изменяют своего ритма. Это казалось столь очевидным, что едва ли было достойно упоминания. Но ничто не должно считаться слишком очевидным; если мы действительно желаем быть осторожными, мы должны подвергать анализу все положения, принимаемые в физике.

Нельзя считать какое-либо положение бессмысленным только потому, что оно отличается от положения классической физики. Мы можем легко представить себе, что движущиеся часы изменяют свой ритм, если закон этого изменения одинаков для всех инерциальных систем.

Еще один пример. Возьмем метровый стержень; это значит, что длина стержня — один метр, пока он находится в покоящейся системе координат. Пусть он движется прямолинейно и равномерно, скользя вдоль масштаба, представляющего систему координат. Будет ли его длина и в этом случае равна одному метру? Мы должны знать заранее, как определять его длину. Пока стержень был в покое, его концы совпадали с нанесенными на масштабе отметками, расстояние между которыми равнялось одному метру. Из этого мы заключили: длина покоящегося стержня равна одному метру. Как мы измеряем длину этого стержня во время движения? Это можно было бы сделать следующим образом. В данный момент два наблюдателя делают одновременно моментальные фотоснимки начала движущегося стержня и его конца. Поскольку снимки берутся одновременные, мы можем сравнить, с какими отметками масштаба совпадают начало и конец движущегося стержня. Таким путем мы определим его длину. Нужно, чтобы два наблюдателя отметили одновременные события, происходящие в различных частях данной системы. Нет никаких оснований считать, что результат таких измерений будет таким же, как и в случае, когда отрезок покоится. Поскольку фотографии должны быть сделаны одновременно, а одновременность, как мы знаем, является относительным понятием, зависящим от системы координат, то кажется вполне возможным, что результаты этих измерений будут различными в различных системах, движущихся друг относительно друга.

Мы легко можем представить себе, что не только движущиеся часы изменяют свой ритм, но и движущийся стержень тоже изменяет свою длину, если законы изменений одинаковы для всех инерциальных систем координат.

Мы лишь обсуждали некоторые новые возможности, не приводя каких-либо оправданий в пользу их принятия.

Мы помним: скорость света одинакова во всех инерциальных системах координат. Этот факт несовместим с классическим преобразованием. Круг должен быть где-то разорван. Нельзя ли это сделать как раз здесь? Не можем ли мы предположить, что имеют место такие изменения в ритме движущихся часов и в длине движущегося стрежня, что постоянство скорости света будет следовать непосредственно из этих предположений? В самом деле, можем! Здесь впервые теория относительности и классическая физика радикально расходятся. Наш довод может быть сформулирован иначе: если скорость света одинакова во всех системах, то движущиеся стрежни должны изменять свою длину, движущиеся часы должны изменять свой ритм, а законы, управляющие этими изменениями, являются строго определенными.

Во всем этом нет ничего таинственного или неразумного. В классической физике всегда предполагалось, что часы и в движении, и в покое имеют одинаковый ритм, что масштабы и в движении, и в покое имеют одинаковую длину. Если скорость света одинакова во всех системах координат, если теория относительности справедлива, то мы должны пожертвовать этим положением. Трудно отделаться от глубоко укоренившихся предрассудков, но другого пути нет. С точки зрения теории относительности старые понятия кажутся произвольными. Почему надо верить, как это мы делали раньше, в абсолютное время, текущее одинаково для всех наблюдателей во всех системах? Почему надо верить в неизменяемое расстояние? Время определяется часами, пространственные координаты — масштабами, и результат этих определений может зависеть от поведения этих часов и масштабов, когда они находятся в движении. Нет оснований считать, что они будут вести себя так, как нам этого хотелось бы. Косвенное наблюдение, а именно наблюдение явлений электромагнитного поля, показывает, что движущиеся часы изменяют свой ритм, а масштаб — длину, в то время как, основываясь на механических явлениях, мы не думали, чтобы это имело место. Мы должны принять понятие относительного времени в каждой системе координат, ибо это наилучший выход из трудностей. Дальнейший научный успех, достигнутый теорией относительности, показывает, что новый взгляд не должен рассматриваться как печальная необходимость, ибо успехи теории относительности оказались весьма значительными.

До сих пор мы старались показать, что привело к основным положениям теории относительности и как теория относительности вынуждала нас пересматривать и изменять классическое преобразование, по-новому трактуя понятия времени и пространства. Наша цель — указать идеи, образующие основу новых физических и философских взглядов. Эти идеи просты; но в той форме, в которой они здесь сформулированы, они недостаточны для того, чтобы получить выводы не только качественные, но и количественные. Мы опять должны применить наш старый метод объяснения только принципиальных идей и формулировки некоторых выводов без доказательства.

Чтобы сделать ясным различие между взглядом старого физика (назовем его С), верящего в классическое преобразование, и взглядом нового физика (назовем его Н), признающего теорию относительности, вообразим между ними следующий диалог.

С. Я верю в принцип относительности Галилея в механике, ибо я знаю, что законы механики одинаковы в двух системах, движущихся прямолинейно и равномерно друг относительно друга, или, другими словами, что эти законы инвариантны относительно классического преобразования.

Н. Но принцип относительности следует применять ко всем событиям внешнего мира. Не только законы механики, но и все законы природы должны быть одинаковы в системах, движущихся прямолинейно и равномерно друг относительно друга.

С. Но как все законы природы могут оказаться одинаковыми в системах, движущихся друг относительно друга? Ведь уравнения поля, т. е. уравнения Максвелла, неинвариантны относительно классического преобразования. Это ясно обнаруживается на примере скорости света. Согласно классическому преобразованию эта скорость не была бы одинаковой в двух системах, движущихся друг относительно друга.

Н. Это только показывает, что классическое преобразование нельзя применять, что связь между двумя системами координат должна быть иной, и что мы не можем связывать координаты и скорости в разных системах координат так, как это сделано в этих законах преобразования. Мы должны заменить их новыми законами, выведя последние из основных положений теории относительности. Не будем заботиться о математическом выражении этих новых законов преобразования и удовлетворимся тем, что они отличны от классического. Мы назовем их кратко преобразованиями Лоренца. Можно показать, что уравнения Максвелла, т. е. законы поля, инвариантны по отношению к преобразованиям Лоренца, подобно тому, как законы механики инвариантны по отношению к классическим преобразованиям. Вспомним, как обстояло дело в классической физике. Мы имели законы преобразования для координат, законы преобразования для скоростей, но законы механики были одинаковы для обеих систем координат, движущихся прямолинейно и равномерно относительно друг друга. У нас были законы преобразования для пространства, но не для времени, потому что время было одинаково во всех системах координат. Однако здесь, в теории относительности, оно различно. Здесь мы имеем законы преобразования пространства, времени и скоростей, отличающиеся от классических законов. Но законы природы опять должны быть одинаковы во всех системах координат, движущихся прямолинейно и равномерно друг относительно друга. Законы природы должны быть инвариантны, но не по отношению к классическим преобразованиям, как прежде, а по отношению к новому типу преобразований — так называемым преобразованиям Лоренца. Во всех инерциальных системах справедливы те же самые законы, а переход от одной системы к другой дается преобразованиями Лоренца.

С. Я верю вам, но мне интересно было бы знать различие между преобразованиями классическими и преобразованиями Лоренца.

Н. Ответить на ваш вопрос лучше всего следующим образом. Сошлемся на некоторые характерные черты классических преобразований, и я постараюсь объяснить, сохраняются ли они в преобразованиях Лоренца, и если нет, то как они изменяются.

С. Если что-либо происходит в какой-то точке пространства в некоторый момент времени в моей системе координат, то наблюдатель, находящийся в другой системе координат, движущейся прямолинейно и равномерно относительно моей, отмечает другое число, определяющее положение места, где происходит событие, но, конечно, то же самое время. Мы употребляем одни и те же часы во всех системах независимо от того, движутся ли они или нет. Это и с вашей точки зрения справедливо?

Н. О, нет. Каждая система координат должна быть снабжена собственными часами, покоящимися в ней, так как движение изменяет ритм часов. Два наблюдателя, находящиеся в различных системах координат, отмечают не только различные числа, определяющие положение, но и различные числа, определяющие время, в которое происходит это событие.

С. Это означает, что время не является больше инвариантом. В классических преобразованиях время всегда одно и то же во всех системах. В преобразованиях Лоренца оно изменяется и ведет себя аналогично координате в старых преобразованиях. Интересно знать, как обстоит дело с длиной. Согласно классической механике твердый стержень сохраняет свою длину как в движении, так и в покое. Верно ли это теперь?

Н. Неверно. В самом деле, из преобразований Лоренца следует, что движущийся стержень сокращается в направлении движения, и сокращение тем больше, чем больше скорость. Чем быстрее движется стержень, тем короче он оказывается. Но такое сокращение происходит только в направлении движения. На рисунке 57 вы видите стержень, который сокращается до половины своей первоначальной длины, когда он движется со скоростью, приближающейся к 0,9 скорости света. Однако в направлении, перпендикулярном к движению, сокращения нет, что я и постарался проиллюстрировать на рисунке 58.

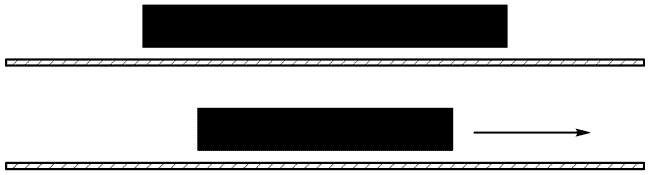
Рис. 57.

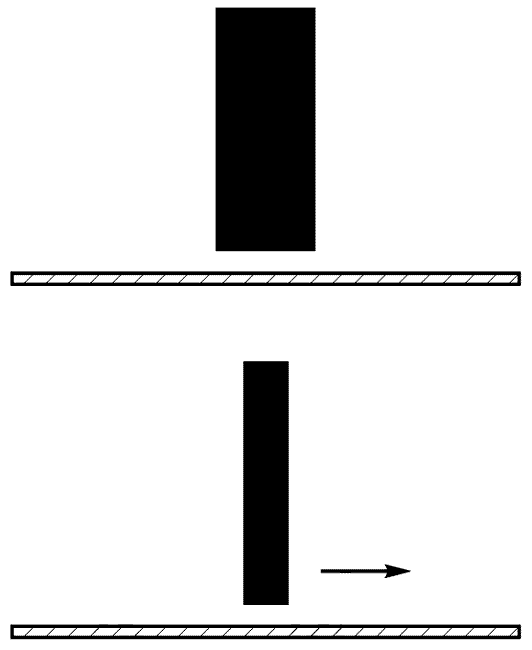
Рис. 58.

С. Это означает, что ритм движущихся часов и длина движущихся стержней зависят от скорости. Но каким образом?

Н. Изменение становится более заметным по мере возрастания скорости. Из преобразований Лоренца следует, что стрежень сократится до нуля, если его скорость достигнет скорости света. Аналогично этому ритм движущихся часов замедляется сравнительно с часами, мимо которых они проходят вдоль стержня; часы совершенно остановились бы, если бы они могли двигаться со скоростью света.

С. Это кажется противоречащим всему нашему опыту. Мы знаем, что вагон не становится короче, когда он в движении, и мы знаем также, что машинист всегда может сравнить свои «хорошие» часы с часами, мимо которых он проезжает, находя, что они хорошо согласованы друг с другом, вопреки вашему утверждению.

Н. Это, конечно, верно. Но все скорости в механике очень малы сравнительно со скоростью света, поэтому нелепо применять теорию относительности к этим явлениям. Каждый машинист может спокойно применять классическую физику, даже если он увеличит свою скорость в сотни тысяч раз. Мы могли бы ожидать несогласия между экспериментом и классическими преобразованиями только в случае скоростей, приближающихся к скорости света. Справедливость преобразований Лоренца может быть проверена лишь при очень больших скоростях.

С. Но имеется и другая трудность. Согласно механике я могу вообразить тела, обладающие скоростями, даже большими, чем скорость света. Тело, движущееся со скоростью света относительно плывущего корабля, движется со скоростью, большей, чем скорость света, относительно берега. Что произойдет со стержнем, который сократился до нуля, когда его скорость сравнялась со скоростью света? Едва ли мы можем ожидать отрицательной длины, если скорость стержня больше скорости света.

Н. В действительности нет никакого основания для такой иронии! С точки зрения теории относительности материальные тела не могут иметь скорости, большей, чем скорость света. Скорость света образует верхний предел скоростей для всех материальных тел. Если скорость тела относительно корабля равна скорости света, то и относительно берега она тоже будет равна скорости света. Простой механический закон сложения и вычитания скоростей больше несправедлив или, более точно, справедлив лишь приближенно для малых скоростей, но не для скоростей, близких к скорости света. Число, выражающее скорость света, явно входит в преобразования Лоренца и играет роль предельного случая, подобно бесконечной скорости в классической механике. Эта более общая теория не противоречит классическим преобразованиям и классической механике. Наоборот, к старым понятиям мы возвращаемся, как к предельному случаю, когда скорости малы. С точки зрения новой теории ясно, в каких случаях справедлива классическая физика и где лежат ее пределы. Было бы нелепо применять теорию относительности к движению автомобилей, пароходов и поездов, как нелепо употреблять счетную машину там, где вполне достаточна таблица умножения.

Относительность и механика.

Теория относительности необходимо возникает из серьезных и глубоких противоречий в старой теории, из которых, казалось, не было выхода. Сила новой теории заключается в согласованности и простоте, с которой она разрешает все эти трудности, используя лишь немногие очень убедительные предположения.

Хотя теория возникла из проблемы поля, она должна охватить все физические законы. Трудность, по-видимому, появляется здесь. Законы поля, с одной стороны, и законы механики — с другой, имеют совершенно различный характер. Уравнения электромагнитного поля инвариантны по отношению к преобразованиям Лоренца, а уравнения механики инвариантны по отношению к классическим преобразованиям. Но теория относительности требует, чтобы все законы природы были инвариантны по отношению к лоренцовым, а не классическим преобразованиям. Последние являются лишь специальным, предельным случаем преобразований Лоренца, когда относительные скорости обеих систем координат очень малы. Если это так, то классическую механику следует изменить, чтобы согласовать ее с требованиями инвариантности по отношению к преобразованиям Лоренца. Или, другими словами, классическая механика не может быть справедливой, если скорости приближаются к скорости света. Переход от одной системы координат к другой может осуществляться только единственным путем — через преобразования Лоренца.

Классическую механику нетрудно было изменить так, чтобы она не противоречила ни теории относительности, ни изобилию материала, полученного наблюдением и объясненного классической механикой. Старая механика справедлива для малых скоростей и образует предельный случай новой механики.

Интересно рассмотреть какой-либо пример изменения в классической механике, которое вносит теория относительности. Возможно, это приведет нас к некоторым выводам, которые могут быть подтверждены или опровергнуты экспериментом.

Предположим, что тело, имеющее определенную массу, движется вдоль прямой и подвергается воздействию внешней силы, действующей в направлении движения. Сила, как мы знаем, пропорциональна изменению скорости. Или, чтобы сказать яснее: не имеет значения, увеличивает ли данное тело свою скорость за одну секунду со 100 до 101 метра в секунду, или от 100 километров до 100 километров и одного метра в секунду, или от 300 000 километров до 300 000 километров и одного метра в секунду. Сила, необходимая для сообщения данному телу какого-либо определенного изменения скорости, всегда одна и та же.

Верно ли это положение с точки зрения теории относительности? Никоим образом! Этот закон справедлив только для малых скоростей. Каков же, по теории относительности, закон для больших скоростей, приближающихся к скорости света? Если скорость велика, то необходима чрезвычайно большая сила, чтобы увеличить ее. Вовсе не одно и то же — увеличить ли на один метр в секунду скорость, равную примерно 100 метрам в секунду, или же скорость, приближающуюся к световой. Чем ближе скорость к скорости света, тем труднее ее увеличить. Когда скорость равна скорости света, то уже невозможно увеличить ее дальше. Таким образом, то новое, что вносит теория относительности, не является удивительным. Скорость света есть верхний предел для всех скоростей. Никакая конечная сила, как бы велика она ни была, не может вызвать увеличения скорости сверх этого предела. На место старого закона механики, связывающего силу и изменение скорости, появляется более сложный закон. С нашей новой точки зрения классическая механика проста потому, что почти во всех наблюдениях мы имеем дело со скоростями, значительно меньшими, чем скорость света.

Покоящееся тело имеет определенную массу, так называемую массу покоя. Мы знаем из механики, что всякое тело сопротивляется изменению его движения; чем больше масса, тем сильнее сопротивление, и чем меньше масса, тем слабее сопротивление. Но в теории относительности мы имеем нечто большее. Тело сопротивляется изменению сильнее не только в случае, когда больше масса покоя, но и в случае, когда его скорость больше. Тела, скорости которых приближались бы к скорости света, оказывали бы очень сильное сопротивление внешним силам. В классической механике сопротивление данного тела есть всегда нечто неизменное, характеризуемое только его массой. В теории относительности оно зависит и от массы покоя, и от скорости. Сопротивление становится бесконечно большим по мере того, как скорость приближается к скорости света.

Только что указанные выводы позволяют нам подвергнуть теорию экспериментальной проверке. Оказывают ли снаряды, движущиеся со скоростями, близкими к скорости света, сопротивление действию внешней силы там, как это предсказывает теория? Так как положения теории относительности имеют в этом отношении количественный характер, то мы могли бы подтвердить или опровергнуть теорию, если бы мы обладали снарядами, движущимися со скоростями, близкими к скорости света.

На самом деле мы находим в природе снаряды, движущиеся с такими скоростями. Атомы радиоактивного вещества, например радия, действуют подобно батарее, которая стреляет снарядами, движущимися с огромными скоростями. Не входя в детали, мы можем указать только на один из самых важных взглядов современной физики и химии. Все вещество в мире построено из элементарных частиц, число разновидностей которых невелико. Подобно этому в одном городе здания различны по величине, конструкции и архитектуре, но на постройку всех их, от хижины до небоскреба, использованы кирпичи лишь очень немногих сортов, одинаковых во всех зданиях. Так, все известные химические элементы нашего материального мира — от легчайшего водорода до наиболее тяжелого урана — построены из одинакового рода кирпичей, т. е. одинакового рода элементарных частиц. Наиболее тяжелые элементы — наиболее сложные построения — неустойчивы, и они распадаются или, как мы говорим, — они радиоактивны. Некоторые кирпичи, т. е. элементарные частицы, из которых состоят радиоактивные атомы, выбрасываются иногда с очень большими скоростями, близкими к скорости света. Атом элемента, скажем, радия, согласно нашим современным взглядам, подтверждаемым многочисленными экспериментами, обладает сложной структурой, и радиоактивный распад является одним из тех явлений, в которых выявляется, что атом построен из более простых кирпичей — элементарных частиц.

С помощью очень остроумных и сложных экспериментов мы можем обнаружить, как частицы сопротивляются действию внешней силы. Эксперименты показывают, что сопротивление, оказываемое этими частицами, зависит от скорости и как раз так, как это предсказывается теорией относительности. Во многих других случаях, где можно было обнаружить зависимость сопротивления от скорости, было установлено полное согласие между теорией относительности и экспериментом. Мы еще раз видим существенные черты творческой работы в науке: предсказание определенных фактов теорией и подтверждение их экспериментом.

Этот результат приводит к дальнейшему важному обобщению. Покоящееся тело имеет массу, но не имеет кинетической энергии, т. е. энергии движения. Движущееся тело имеет и массу, и кинетическую энергию. Оно сопротивляется изменению скорости сильнее, чем покоящееся тело. Кажется, что как будто кинетическая энергия движущегося тела увеличивает его сопротивление. Если два тела имеют одинаковую массу покоя, то тело с большей кинетической энергией сопротивляется действию внешней силы сильнее.

Представим себе ящик, наполненный шарами; пусть ящик и шары покоятся в нашей системе координат. Чтобы привести его в движение, чтобы увеличить его скорость, требуется некоторая сила. Но будет ли эта сила производить то же самое увеличение скорости за тот же промежуток времени, если шары в ящике будут быстро двигаться по всем направлениям, подобно молекулам в газе, со средними скоростями, близкими к скорости света? Теперь необходима будет большая сила, так как возросшая кинетическая энергия шаров усиливает сопротивление ящика. Энергия, во всяком случае кинетическая энергия, сопротивляется движению так же, как и весомая масса. Справедливо ли это и в отношении всех видов энергии?

Теория относительности, исходя из своих основных положений, дает ясный и убедительный ответ на этот вопрос, ответ опять-таки количественного характера: всякая энергия сопротивляется изменению движения; всякая энергия ведет себя подобно веществу; кусок железа весит больше, когда он раскален докрасна, чем когда он холоден; излучение, испускаемое Солнцем и проходящее через пространство, содержит энергию и поэтому имеет массу; Солнце и все излучающие звезды теряют массу вследствие излучения. Это заключение, совершенно общее по своему характеру, является важным достижением теории относительности и соответствует всем фактам, которые привлекались для его проверки.

Классическая физика допускала две субстанции: вещество и энергию. Первое имело вес, а вторая была невесома. В классической физике мы имели два закона сохранения: один для вещества, другой для энергии. Мы уже ставили вопрос о том, сохраняет ли еще современная физика этот взгляд на две субстанции и два закона сохранения. Ответ таков: нет. Согласно теории относительности нет существенного различия между массой и энергией. Энергия имеет массу, а масса представляет собой энергию. Вместо двух законов сохранения мы имеем только один: закон сохранения массы-энергии. Этот новый взгляд оказался очень плодотворным в дальнейшем развитии физики.

Как это случилось, что тот факт, что энергия обладает массой, а масса представляет собой энергию, столь долго оставался неизвестным? Весит ли кусок нагретого железа больше, чем кусок холодного? Теперь мы отвечаем «да», а раньше отвечали «нет». Страницы, лежащие между этими двумя ответами, разумеется, не могут скрыть этого противоречия.

Трудности, стоящие здесь перед нами, того же порядка, какие встречались нам и прежде. Изменение массы, предсказанное теорией относительности, неизмеримо мало, его нельзя обнаружить прямым взвешиванием даже с помощью очень чувствительных весов. Доказательство того, что энергия не невесома, можно получить многими очень убедительными, но косвенными путями.

Причина этого недостатка непосредственной очевидности состоит в очень малой величине взаимообмена между веществом и энергией. Энергия по отношению к массе подобна обесцененной валюте, взятой по отношению к валюте высокой ценности. Один пример сделает это ясным. Количество теплоты, способное превратить тридцать тысяч тонн воды в пар, весило бы около одного грамма. Энергия столь долго считалась невесомой просто потому, что масса, которую она представляет, слишком мала.

Старая энергия-субстанция есть вторая жертва теории относительности. Первой была среда, в которой распространялись световые волны.

Влияние теории относительности выходит далеко за пределы тех проблем, из которых она возникла. Она снимает трудности и противоречия теории поля; она формулирует более общие механические законы; она заменяет два закона сохранения одним; она изменяет наше классическое понятие абсолютного времени. Ее ценность не ограничивается лишь сферой физики; она образует общий остов, охватывающий все явления природы.

Пространственно-временн?й континуум.

«Французская революция началась в Париже 14 июля 1789 года». В этом предложении установлены место и время события. Тому, кто слышит это утверждение впервые и кто не знает, что значит «Париж», можно было бы сказать: это — город на нашей земле, расположенный на 2° восточной долготы и 49° северной широты. Два числа характеризовали бы тогда место, а «14 июля 1789 года» — время, в которое произошло событие. В физике точная характеристика, когда и где произошло событие, чрезвычайно важна, гораздо важнее, чем в истории, так как эти числа образуют основу количественного описания.

Ради простоты мы рассматривали прежде только движение вдоль прямой. Нашей координатной системой был твердый стержень с началом, но без конца. Сохраним это ограничение. Отметим на стержне различные точки; положение каждой из них может быть охарактеризовано только одним числом — координатой точки. Сказать, что координата точки равна 7,586 метра, означает, что ее расстояние от начала стержня равно 7,586 метра. Наоборот, если кто-то задает мне любое число и единицу измерения, я всегда могу найти точку на стержне, соответствующую этому числу. Мы видим, что каждому числу соответствует определенная точка на стержне, а каждой точке соответствует определенное число. Этот факт выражается математиками в следующем предложении: все точки стержня образуют одномерный континуум. Тогда существует точка, сколь угодно близкая к данной точке стержня. Мы можем связать две отдаленные точки на стержне рядом отрезков, расположенных один за другим, каждый из которых сколь угодно мал. Таким образом, тот факт, что отрезки, связывающие отдаленные точки, произвольно малы, является характеристикой континуума.

Возьмем другой пример. Пусть мы имеем плоскость или, если вы предпочитаете что-либо более конкретное, поверхность прямоугольного стола (рис. 59).

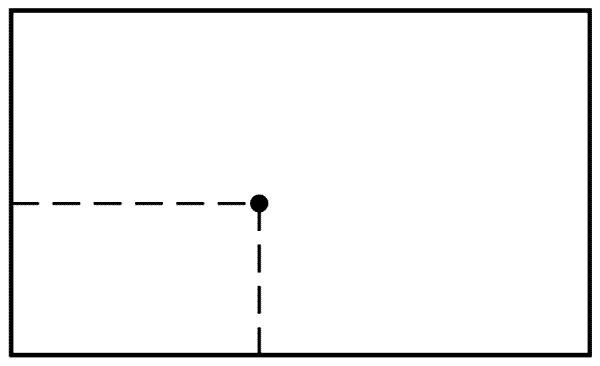
Рис. 59.

Положение точки на этом столе можно охарактеризовать двумя числами, а не одним, как раньше. Два числа суть расстояния от двух перпендикулярных краев стола. Не одно число, а пара чисел соответствует каждой точке плоскости; каждой паре чисел соответствует определенная точка. Другими словами, плоскость есть двухмерный континуум. Тогда существуют точки, сколь угодно близкие к данной точке плоскости. Две отдаленные точки могут быть связаны кривой, разделенной на отрезки, сколь угодно малые. Таким образом, произвольная малость отрезков, последовательно укладывающихся на кривой, связывающей две отдаленные точки, каждая из которых может быть определена двумя числами, снова является характеристикой двухмерного континуума.

Еще один пример. Представим себе, что вы хотите в качестве системы координат рассматривать свою комнату. Это означает, что вы хотите любое положение тела определить относительно стен комнаты. Положение кончика лампы, если она в покое, может быть описано тремя числами: два из них определяют расстояние от двух перпендикулярных стен, а третье — расстояние от пола или потолка. Каждой точке пространства соответствуют три определенных числа; каждым трем числам соответствует определенная точка в пространстве (рис. 60).

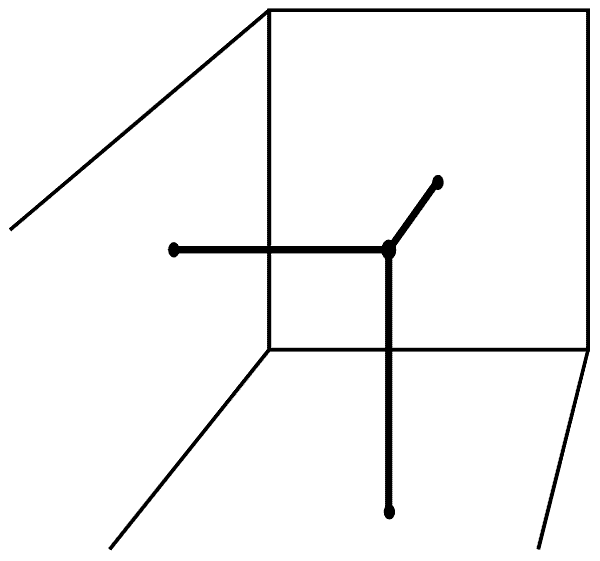
Рис. 60.

Это выражается предположением: наше пространство есть трехмерный континуум. Существуют точки, весьма близкие к каждой данной точке пространства. И опять произвольная малость отрезков линии, связывающей отдаленные точки, каждая из которых представлена тремя числами, есть характеристика трехмерного континуума.

Но все это едва ли физика. Чтобы вернуться к физике, нужно рассмотреть движение материальных частиц. Чтобы исследовать и предсказывать явления в природе, необходимо рассматривать не только место, но и время физических событий. Возьмем снова очень простой пример.

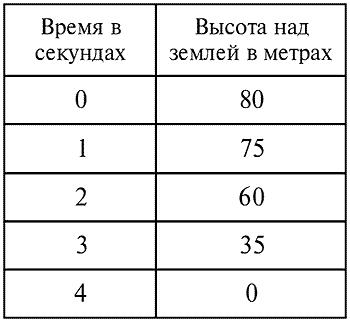
Маленький камешек, который примем за частицу, падает с башни. Допустим, что высота башни равна 80 метрам. Со времен Галилея мы в состоянии предсказать координаты камня в произвольный момент времени после начала его падения.

На текущей стр[анице] представлена «временн?я таблица», приближенно описывающая положение камня после 1, 2, 3 и 4 секунд[211].

В нашей «временн?й таблице» зарегистрированы пять событий, каждое из которых представлено двумя числами — временем и пространственной координатой каждого события. Первое событие есть начало движения камня с высоты 80 метров от земли в момент, равный нулю. Второе событие есть совпадение камня с нашим твердым стержнем (башней) на высоте 75 метров от земли. Это имеет место по истечении одной секунды. Последнее событие есть удар камня о землю.

Те сведения, которые записаны во «временн?й таблице», можно было бы представить иначе. Пять пар чисел ее можно было бы представить, как пять точек на плоскости. Установим сначала масштаб. Например: пусть один отрезок будет представлять метр, а другой секунду (рис. 61).

Рис. 61.

Затем нарисуем две перпендикулярные линии, одну из них, скажем, горизонтальную, назовем временн?й осью, вертикальную же — пространственной осью. Мы сразу же видим, что нашу «временн?ю таблицу» можно представить пятью точками в пространственно-временн?й плоскости (рис. 62).

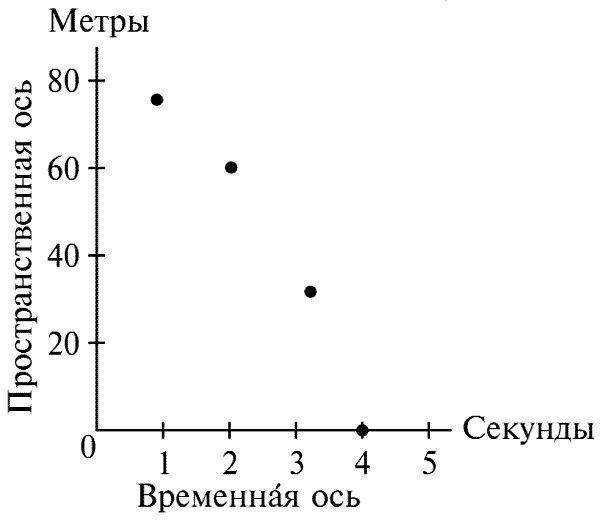
Рис. 62.

Расстояние точек от пространственной оси представляют собой координаты времени, указанные в первой колонке «временн?й таблицы», а расстояния от оси времен — их пространственные координаты.

Одна и та же связь выражена двумя способами: с помощью «временн?й таблицы» и точками на плоскости. Одно может быть построено из другого. Выбор между этими двумя представлениями является делом лишь вкуса, ибо в действительности они оба эквивалентны.

Сделаем теперь еще один шаг. Представим себе улучшенную «временн?ю таблицу», дающую положения не для каждой секунды, а, скажем, для каждой сотой или тысячной доли секунды. Тогда у нас будет много точек в нашей пространственно-временн?й плоскости. Наконец, если положение дается для каждого мгновения или, как говорят математики, если пространственная координата дается как функция времени, то совокупность точек становится непрерывной линией. Поэтому наш следующий рисунок дает не отрывочные сведения, как прежде, а полное представление о движении камня (рис. 63).

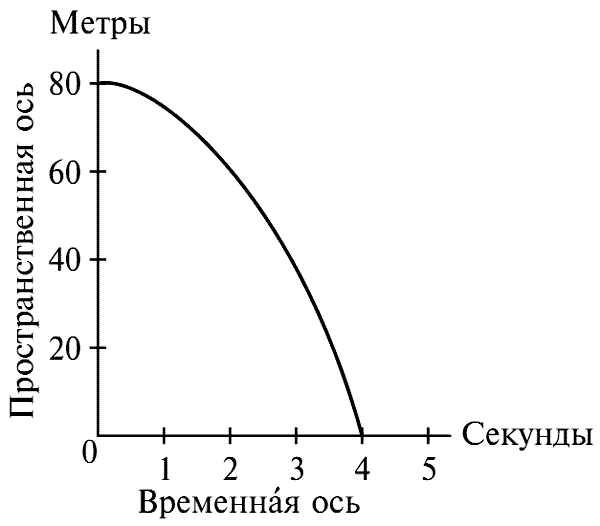
Рис. 63.

Движение вдоль твердого стрежня (башни), т. е. движение в одномерном пространстве, представлено здесь в виде кривой в двухмерном пространственно-временн?м континууме. Каждой точке в нашем пространственно-временн?м континууме соответствует пара чисел, одно из которых отмечает временн?ю, а другое — пространственную координату. Наоборот: определенная точка в нашем пространственно-временн?м континууме соответствует некоторой паре чисел, характеризующей событие. Две соседние точки представляют собой два события, происшедшие в местах, близких друг от друга, и в моменты времени, непосредственно следующие друг за другом.

Вы могли бы возразить против нашего способа представления следующим образом: мало смысла в представлении единицы времени отрезком, в его механическом соединении с пространством, образующим двухмерный континуум из двух одномерных континуумов. Но тогда вы должны были бы столь же серьезно протестовать против всех графиков, представляющих, например, изменение температуры в Нью-Йорке в течение последнего лета, или против графиков, изображающих изменение стоимости жизни за последние несколько лет, так как в каждом из этих случаев употребляется тот же самый метод. В температурных графиках одномерный температурный континуум соединяется с одномерным временны?м континуумом в двухмерный температурно-временн?й континуум.

Вернемся к частице, падающей с 80-метровой башни. Наша графическая картина движения есть полезное соглашение, так как она позволяет нам характеризовать положение частицы в любой произвольный момент времени. Зная, как движется частица, мы хотели бы изобразить ее движение еще раз. Сделать это можно двумя путями.

Вспомним изображение частиц, изменяющих свое положение со временем в одномерном пространстве. Мы изображаем движение как ряд событий в одномерном пространственном континууме. Мы не смешиваем время и пространство, применяя динамическую картину, в которой положения изменяются со временем.

Но можно изобразить то же самое движение другим путем. Мы можем образовать статическую картину, рассматривая кривую в двухмерном пространственно-временн?м континууме. Теперь движение рассматривается как нечто, что есть, что существует в двухмерном пространственно-временн?м континууме, а не как нечто, изменяющееся в одномерном пространственном континууме.

Обе эти картины совершенно равноценны, и предпочтение одной из них перед другой есть дело лишь соглашения и вкуса.

То, что здесь сказано о двух картинах движения, не имеет отношения к теории относительности. Оба представления могут быть использованы с одинаковым правом, хотя классическая теория скорее предпочитала динамическую картину описания движения, как того, что происходит в пространстве, статической картине, описывающей его в пространстве-времени. Но теория относительности изменила этот взгляд. Она явно предпочла статическую картину и нашла в этом представлении движения, как того, что существует в пространстве-времени, более удобную и более объективную картину реальности. Мы должны еще ответить на вопрос, почему эти две картины эквивалентны с точки зрения классической физики и не эквивалентны с точки зрения теории относительности. Ответ будет понятным, если снова рассмотреть две системы координат, движущиеся прямолинейно и равномерно друг относительно друга.

Согласно классической физике наблюдатели в обеих системах, движущихся прямолинейно и равномерно друг относительно друга, найдут для одного и того же события различные пространственные координаты, но одну и ту же временн?ю координату. Таким образом, в нашем примере удар камня о землю характеризуется при нашем выборе системы координат временн?й координатой «4» и пространственной координатой «0». Согласно классической механике наблюдатели, движущиеся прямолинейно и равномерно относительно выбранной системы координат, обнаружат, что камень достигнет земли спустя четыре секунды после начала падения. Но каждый из наблюдателей относит расстояние к своей системе координат, и они будут, вообще говоря, связывать различные пространственные координаты с событием соударения, хотя временн?я координата будет одной и той же для всех других наблюдателей, движущихся прямолинейно и равномерно друг относительно друга. Классическая физика знает только «абсолютное» время, текущее одинаково для всех наблюдателей. Для каждой системы координат двухмерный континуум может быть разбит на два одномерных континуума: время и пространство. Благодаря «абсолютному» характеру времени переход от «статики» к «динамической» картине движения имеет в классической физике объективный смысл.

Но мы уже убедились в том, что классические преобразования не могут применяться в физике в общем случае. С практической точки зрения они еще пригодны для малых скоростей, но не годятся для обоснования фундаментальных физических вопросов.

Согласно теории относительности момент соударения камня с землей не будет одним и тем же для всех наблюдателей. И временн?я координата, и пространственная координата будут различными в двух различных системах координат, и изменение временн?й координаты будет весьма заметным, если относительная скорость систем приближается к скорости света. Двухмерный континуум не может быть разбит на два одномерных континуума как в классической физике. Мы не можем рассматривать пространство и время раздельно при определении пространственно-временны?х координат в другой системе координат. Разделение двухмерного континуума на два одномерных оказывается, с точки зрения теории относительности, произвольным процессом, не имеющим объективного смысла.

Все, что мы только что сказали, нетрудно обобщить для случая движения, не ограниченного прямой линией. В самом деле, для описания событий в природе нужно применить не два, а четыре числа. Физическое пространство, постигаемое через объекты и их движения, имеет три измерения, и положения объектов характеризуются тремя числами. Момент события есть четвертое число. Каждому событию соответствует четыре определенных числа; каким-либо четырем числам соответствует определенное событие. Поэтому мир событий образует четырехмерный континуум. В этом нет ничего мистического, и последнее предложение одинаково справедливо и для классической физики, и для теории относительности. И опять различие обнаруживается лишь тогда, когда рассматриваются две системы координат, движущиеся друг относительно друга. Пусть движется комната, а наблюдатели внутри и вне ее определяют пространственно-временны?е координаты одних и тех же событий. Сторонник классической физики разобьет четырехмерный континуум на трехмерное пространство и одномерный временн?й континуум. Старый физик заботится только о преобразовании пространства, так как время для него абсолютно. Он находит разбиение четырехмерного мирового континуума на пространство и время естественным и удобным. Но с точки зрения теории относительности время, так же как и пространство, изменяется при переходе от одной системы координат к другой, и преобразования Лоренца рассматривают трансформационные свойства четырехмерного пространственно-временн?го континуума — нашего четырехмерного мира событий.

Мир событий может быть описан динамически с помощью картины, изменяющейся во времени и набросанной на фоне трехмерного пространства. Но он может быть также описан посредством статической картины, набросанной на фоне четырехмерного пространственно-временн?го континуума. С точки зрения классической физики обе картины, динамическая и статическая, — равноценны. Но с точки зрения теории относительности статическая картина более удобна и более объективна.

Даже в теории относительности мы можем еще употреблять динамическую картину, если мы ее предпочитаем. Но мы должны помнить, что это деление на время и пространство не имеет объективного смысла, так как время больше не является «абсолютным». Дальше мы еще будем пользоваться «динамическим», а не «статическим» языком, но при этом всегда будем учитывать его ограниченность.

Общая относительность.

Остается выяснить еще один момент. Пока еще не решен один из наиболее фундаментальных вопросов: существует ли инерциальная система? Мы узнали кое-что о законах природы, их инвариантности по отношению к преобразованиям Лоренца и их справедливости во всех инерциальных системах, движущихся прямолинейно и равномерно друг относительно друга. Мы имеем законы, но не знаем того «тела отсчета», к которому следует их отнести.

Для того чтобы больше знать об этих трудностях, побеседуем с физиком, стоящим на позиции классической физики, и зададим ему несколько простых вопросов:

— Что такое инерциальная система?

— Это система координат, в которой справедливы законы механики. Тело, на которое не действуют внешние силы, движется в такой системе прямолинейно и равномерно. Это свойство позволяет нам, следовательно, отличить инерциальную систему координат от всякой другой.

— Но что значит, что на тело не действуют никакие внешние силы?

— Это просто значит, что тело движется прямолинейно и равномерно в инерциальной системе координат.

Здесь вы могли бы еще раз поставить вопрос: «Что же такое инерциальная система координат?» Но поскольку имеется мало надежд получить ответ, отличный от вышеприведенного, постараемся добиться конкретной информации, изменив вопрос:

— Является ли система, жестко связанная с Землей, инерциальной?

— Нет, потому что законы механики не являются строго справедливыми на Земле благодаря ее вращению. Систему координат, жестко связанную с Солнцем, можно считать инерциальной при решении многих проблем; но когда мы говорим о вращении Солнца, мы снова заключаем, что жестко связанную с ним систему координат нельзя считать строго инерциальной.

— Тогда что конкретно является вашей инерциальной системой координат и как следует выбрать состояние ее движения?

— Это только полезная фикция, и у меня нет никакого представления о том, как ее реализовать. Если бы только я мог изолироваться от всех материальных тел и освободиться от всех внешних влияний, то моя система координат была бы инерциальной.

— Но что вы имеете в виду, говоря о системе координат, свободной от всех внешних влияний?

— Я имею в виду, что система координат инерциальна. — Мы вновь вернулись к нашему первоначальному вопросу!

Наша беседа обнаруживает серьезную трудность в классической физике. Мы имеем законы, но не знаем, каково то тело отсчета, к которому следует их отнести, и все наше физическое построение оказывается возведенным на песке.

Мы можем подойти к той же трудности с другой точки зрения. Постараемся представить себе, что во всей Вселенной существует только одно тело, образующее нашу систему координат. Это тело начинает вращаться. Согласно классической механике физические законы для вращающегося тела отличны от законов для невращающегося тела. Если принцип инерции справедлив в одном случае, то он несправедлив в другом. Но все это звучит очень сомнительно. Позволительно ли рассматривать движение лишь одного тела во всей Вселенной? Под движением тела мы всегда разумеем изменение его положения относительно другого тела. Поэтому говорить о движении одного-единственного тела — значит противоречить здравому смыслу. Классическая механика и здравый смысл сильно расходятся в этом пункте. Рецепт Ньютона таков: если принцип инерции имеет силу, то система координат либо покоится, либо движется прямолинейно и равномерно. Если принцип инерции не имеет силы, то тело не находится в прямолинейном и равномерном движении. Таким образом, наш вывод о движении или покое зависит от того, применимы или нет все физические законы к данной системе координат.

Возьмем два тела, например Солнце и Землю. Движение, которое мы наблюдаем, опять относительное. Его можно описать с помощью системы координат, связанной либо с Землей, либо с Солнцем. С этой точки зрения великое достижение Коперника состоит в переносе системы координат с Земли на Солнце. Но поскольку движение относительно и можно применить любое тело отсчета, то оказывается, что нет никаких оснований для того, чтобы предпочесть одну систему координат другой.

Снова вмешивается физика и изменяет нашу общепринятую точку зрения. Система координат, связанная с Солнцем, имеет с инерциальной системой большее сходство, чем система, связанная с Землей. Физические законы предпочтительнее применять в системе Коперника, чем в системе Птолемея. Величие открытия Коперника может быть высоко оценено лишь с физической точки зрения. Физика показывает, что для описания движения планет система координат, жестко связанная с Солнцем, имеет огромные преимущества.

В классической физике нет никакого абсолютного прямолинейного и равномерного движения. Если две системы координат движутся прямолинейно и равномерно друг относительно друга, то нет никаких оснований говорить: «Эта система покоится, а другая движется». Но если обе системы координат находятся в непрямолинейном и неравномерном движении друг относительно друга, то имеется полное основание сказать: «Это тело движется, а другое покоится (или движется прямолинейно и равномерно)». Абсолютное движение имеет здесь вполне определенный смысл. В этом месте между здравым смыслом и классической физикой имеется широкая пропасть. Упомянутые трудности, касающиеся инерциальной системы, а также и трудности, касающиеся абсолютного движения, тесно связаны между собой. Абсолютное движение становится возможным только благодаря идее об инерциальной системе, для которой справедливы законы природы.

Может показаться, что будто бы нет выхода из этих трудностей, что будто бы никакая физическая теория не может избежать их. Источник их лежит в том, что законы природы справедливы только для особого класса систем координат, а именно для инерциальных. Возможность разрешения этих трудностей зависит от ответа на следующий вопрос: можем ли мы сформулировать физические законы таким образом, чтобы они были справедливыми для всех систем координат, не только для систем, движущихся прямолинейно и равномерно, но и для систем, движущихся совершенно произвольно по отношению друг к другу? Если это можно сделать, то наши трудности будут разрешены. Тогда мы будем в состоянии применять законы природы в любой системе координат. Борьба между воззрениями Птолемея и Коперника, столь жестокая в ранние дни науки, стала бы тогда совершенно бессмысленной. Любая система координат могла бы применяться с одинаковым основанием. Два предложения — «Солнце покоится, а Земля движется» и «Солнце движется, а Земля покоится» — означали бы просто два различных соглашения о двух различных системах координат.

Могли ли бы мы построить реальную релятивистскую физику, справедливую во всех системах координат; физику, в которой имело бы место не абсолютное, а лишь относительное движение? Это, в самом деле, оказывается возможным!

У нас есть по крайней мере одно, хотя и очень слабое, указание о том, как построить новую физику. Действительно, релятивистская физика должна применяться во всех системах координат, а стало быть, и в специальном случае — в инерциальной системе. Мы уже знаем законы для этой инерциальной системы координат. Новые общие законы, справедливые для всех систем координат, должны в специальном случае инерциальной системы сводиться к старым, известным законам.

Проблема формулирования физических законов для всякой системы координат была разрешена так называемой общей теорией относительности; предыдущая теория, применяемая только к инерциальным системам, называется специальной теорией относительности. Эти две теории не могут, разумеется, противоречить друг другу, так как мы всегда должны включать установленные ранее законы специальной теории относительности в общие законы для случая неинерциальной системы. Но если раньше инерциальная система координат была единственной, для которой были сформулированы физические законы, то теперь она будет представлять особый предельный случай, поскольку допустимы любые системы координат, движущиеся произвольно по отношению друг к другу.

Такова программа общей теории относительности. Но, обрисовывая путь, каким она создавалась, мы должны быть еще менее конкретными, чем это было до сих пор. Новые трудности, возникающие в процессе развития науки, вынуждают нашу теорию становиться все более и более абстрактной. Нас ожидает еще ряд неожиданностей. Но наша постоянная конечная цель — все лучшее и лучшее понимание реальности. К логической цепи, связывающей теорию и наблюдение, прибавляются новые звенья. Чтобы очистить путь, ведущий от теории к эксперименту, от ненужных и искусственных допущений, чтобы охватить все более обширную область фактов, мы должны делать цепь все длиннее и длиннее. Чем проще и фундаментальнее становятся наши допущения, тем сложнее математическое орудие нашего рассуждения; путь от теории к наблюдению становится длиннее, тоньше и сложнее. Хотя это и звучит парадоксально, но мы можем сказать: современная физика проще, чем старая физика, и поэтому она кажется более трудной и запутанной. Чем проще наша картина внешнего мира и чем больше фактов она охватывает, тем резче отражает она в наших умах гармонию Вселенной.

Наша новая идея проста: построить физику, справедливую для всех систем координат. Осуществление этой идеи приносит формальное усложнение и вынуждает нас использовать математические методы, отличные от тех, которые до сих пор применялись в физике. Мы покажем здесь только связь между осуществлением этой программы и двумя принципиальными проблемами: тяготением и геометрией.

Вне и внутри лифта.

Закон инерции является первым большим успехом в физике, фактически ее действительным началом. Он был получен размышлением об идеализированном эксперименте, о теле, постоянно движущемся без трения и без воздействия каких-либо других внешних сил. Из этого примера, а позднее из многих других, мы узнали о важности идеализированного эксперимента, созданного мышлением. Здесь тоже будут обсуждаться идеализированные эксперименты. Хотя они и могут выглядеть весьма фантастично, тем не менее они помогут нам понять в относительности столько, сколько это возможно с помощью наших простых методов.

Раньше у нас был идеализированный эксперимент с прямолинейно и равномерно движущейся комнатой. Здесь мы будем иметь дело с падающим лифтом.

Представим себе огромный лифт на башне небоскреба, гораздо более высокого, чем какой-либо из действительно построенных. Внезапно канат, поддерживающий лифт, обрывается, и лифт свободно падает по направлению к земле. Во время падения наблюдатели в лифте производят опыты. Описывая их, мы можем не заботиться о сопротивлении воздуха или трении, потому что в наших идеализированных условиях можно пренебречь их наличием. Один из наблюдателей вынимает платок и часы из своего кармана и выпускает их из рук. Что происходит с этими предметами? Для внешнего наблюдателя, который смотрит через окно лифта, и платок, и часы падают по направлению к земле с одинаковым ускорением. Мы помним, что ускорение падающих тел совершенно независимо от их масс, и это было тем фактом, который обнаружил равенство тяжелой и инертной массы. Мы помним также, что равенство двух масс — тяжелой и инертной — с точки зрения классической механики было совершенно случайным фактом и не играло никакой роли в ее структуре. Однако здесь это равенство, отраженное в равенстве ускорения всех падающих тел, существенно и составляет основу всех наших рассуждений.

Вернемся к падающим платку и часам; для внешнего наблюдателя оба предмета падают с одинаковым ускорением. Но таково же ускорение и лифта, его стен, пола и потолка. Поэтому расстояние между обоими телами и полом не изменится. Для внутреннего наблюдателя оба тела остаются точно там же, где они были в тот момент, когда наблюдатель выпустил их из рук. Внутренний наблюдатель может игнорировать поле тяготения, так как источник последнего лежит вне его системы координат. Он находит, что никакие силы внутри лифта не действуют на оба тела, и, таким образом, они остаются в покое, как если бы они находились в инерциальной системе. Странные вещи происходят в лифте! Если наблюдатель толкает тело в каком-либо направлении, например, вверх или вниз, то оно всегда движется прямолинейно и равномерно, пока не столкнется с потолком или полом лифта. Короче говоря, законы классической механики справедливы для наблюдателя внутри лифта. Все тела ведут себя так, как следовало ожидать по закону инерции. Наша новая система координат, жестко связанная со свободно падающим лифтом, отличается от инерциальной системы лишь в одном отношении. В инерциальной системе координат движущееся тело, на которое не действуют никакие силы, будет вечно двигаться прямолинейно и равномерно. Инерциальная система координат, рассматриваемая в классической физике, не ограничена ни в пространстве, ни во времени. Однако рассматриваемый случай с наблюдателем, находящимся в лифте, иной. Инерциальный характер его системы координат ограничен в пространстве и времени. Рано или поздно прямолинейно и равномерно движущееся тело столкнется со стенками лифта; при этом прямолинейное и равномерное движение нарушится. Рано или поздно весь лифт столкнется с землей, уничтожив наблюдателей и их опыты. Эта система координат является лишь «карманным изданием» реальной инерциальной системы.

Этот локальный характер системы координат весьма существен. Если бы наш воображаемый лифт достигал размеров от Северного полюса до экватора и платок был бы помещен на Северном полюсе, а часы на экваторе, то для внешнего наблюдателя оба тела не имели бы одинакового ускорения; они не были бы в покое друг относительно друга. Все наши рассуждения потерпели бы крушение! Размеры лифта должны быть ограничены так, чтобы можно было предположить равенство ускорений всех тел по отношению к внешнему наблюдателю.

С этим ограничением система координат, связанная с падающим лифтом, инерциальна для внутреннего наблюдателя. По крайней мере мы можем указать систему координат, в которой справедливы все физические законы, хотя она и ограничена во времени и пространстве. Если мы вообразим другую систему координат, другой лифт, движущийся прямолинейно и равномерно относительно свободно падающего, то обе эти системы координат будут локально инерциальными. Все законы совершенно одинаковы в обеих системах. Переход от одной системы к другой дается преобразованием Лоренца.

Посмотрим, каким путем оба наблюдателя, внешний и внутренний, описывают то, что происходит в лифте.

Внешний наблюдатель замечает движение лифта и всех тел в нем и находит его соответствующим закону тяготения Ньютона. Для него движение является не равномерным, а ускоренным вследствие действия поля тяготения земли.

Однако поколение физиков, рожденное и воспитанное в лифте, рассуждало бы совершенно иначе. Оно было бы уверено в том, что оно обладает инерциальной системой, и относило бы все законы природы к своему лифту, заявляя с уверенностью, что законы принимают особенно простую форму в их системе координат. Для них было бы естественным считать свой лифт покоящимся и свою систему координат инерциальной.

Невозможно установить принципиальное различие между внешним и внутренним наблюдателями. Каждый из них мог бы претендовать на право отнести все события к своей системе координат. Оба описания событий можно было бы сделать одинаково последовательными.

Из этого примера мы видим, что последовательное описание физических явлений в двух различных системах координат возможно, даже если они не движутся прямолинейно и равномерно друг относительно друга. Но для такого описания мы должны принять во внимание тяготение, создающее, так сказать, «мост», позволяющий перейти от одной системы координат к другой. Поле тяготения существует для внешнего наблюдателя, для внутреннего наблюдателя оно не существует. Ускоренное движение лифта в поле тяготения существует для внешнего наблюдателя, для внутреннего же наблюдателя — покой и отсутствие поля тяготения. Но «мост», т. е. поле тяготения, делающее описание в обеих системах координат возможным, покоится на одной очень важной опоре: эквивалентности тяжелой и инертной масс. Без этой руководящей идеи, оставшейся незамеченной в классической механике, наши теперешние рассуждения полностью отпали бы.

Возьмем несколько иной идеализированный эксперимент. Пусть имеется инерциальная система координат, в которой справедлив закон инерции. Мы уже описывали то, что происходит в лифте, покоящемся в такой инерциальной системе. Но теперь мы изменим картину. Кто-то извне привязал к лифту канат и тянет его с постоянной силой в направлении, указанном на рисунке 64.

Рис. 64.

Неважно, как это осуществлено. Так как законы механики справедливы в этой системе координат, то лифт в целом движется с постоянным ускорением в направлении движения. Будем опять слушать объяснения явлений, происходящих в лифте, даваемые внешним и внутренним наблюдателями.

Внешний наблюдатель. Моя система координат инерциальна. Лифт движется с постоянным ускорением, потому что подвергается воздействию постоянной силы. Наблюдатели внутри лифта находятся в абсолютном движении, для них законы механики несправедливы. Они не находят, что тела, на которые не действуют силы, покоятся. Если тело остается свободным, оно скоро столкнется с полом лифта, так как пол движется вверх по направлению к телу. Это происходит одинаково и с часами, и с платком. Мне кажется очень странным, что наблюдатель внутри лифта должен всегда быть на «полу», потому что, как только он прыгнет, пол достигнет его вновь.

Внутренний наблюдатель. Я не вижу какого-либо основания считать, что мой лифт находится в абсолютном движении. Я согласен, что моя система координат, жестко связанная с лифтом, фактически не инерциальна, но я не думаю, что это имеет какое-то отношение к абсолютному движению. Мои часы, платок и все тела падают потому, что лифт в целом находится в поле тяготения. Я замечаю движение точно такого же рода, как и человек на Земле. Он объясняет его очень просто — действием поля тяготения. Такое же объяснение подходит и для меня.

Эти два описания — одно данное внешним, а другое — внутренним наблюдателем, — вполне последовательны, и нет возможности решить, какое из них правильно. Мы можем принять любое из них для описания явлений в лифте: либо вместе с внешним наблюдателем принять неравномерность движения и отсутствие поля тяготения, либо вместе с внутренним наблюдателем принять покой и наличие поля тяготения.

Внешний наблюдатель может предположить, что лифт находится в «абсолютном» неравномерном движении. Но движение, которое уничтожается предположением о действии поля тяготения, не может считаться абсолютным.

Возможно, что имеется выход из неопределенности, созданной наличием двух различных описаний, и, может быть, можно было бы вынести решение в пользу одного и против другого. Представим себе, что световой луч входит в лифт горизонтально через боковое окно и спустя очень короткое время достигает противоположной стены. Посмотрим, каковы будут предсказания обоих наблюдателей относительно пути луча.

Внешний наблюдатель, который считает, что лифт находится в ускоренном движении, утверждал бы: световой луч входит в окно и движется горизонтально вдоль прямой с постоянной скоростью по направлению к противоположной стене. Но лифт движется вверх, и за время, в течение которого свет доходит к стене, лифт изменит свое положение. Поэтому свет упадет в точку, расположенную не точно напротив точки его входа, а немного ниже (рис. 65).

Рис. 65.

Смещение будет очень небольшим, но тем не менее оно существует, и световой луч проходит относительно лифта не вдоль прямой, а вдоль слабо искривленной линии. Это вызвано тем, что за то время, когда луч пересекает внутренность лифта, сам лифт смещается на некоторое расстояние.

Внутренний наблюдатель, который считает, что на все объекты в лифте действует поле тяготения, сказал бы: ускоренного движения лифта нет, а есть лишь действие поля тяготения. Луч света невесом и потому не будет подвергаться действию поля тяготения. Если его направить горизонтально, он упадет на стену в точке как раз напротив той, в которую он вошел.

Из этого обсуждения следует, что имеется возможность выбора одной из двух противоположных точек зрения, так как явление различалось бы для обоих наблюдателей. Если ни в одном из только что указанных объяснений нет ничего нелогичного, то все наши предыдущие рассуждения нарушаются, и мы не можем последовательно описывать все явления двумя методами, либо принимая поле тяготения, либо отказываясь от него.

Но, к счастью, в рассуждениях внутреннего наблюдателя имеется серьезная ошибка, спасающая наши предыдущие заключения. Он сказал: «Луч света невесом и потому не будет подвергаться действию поля тяготения». Но это неверно! Луч света несет энергию, а энергия имеет массу. Но на всякую инертную массу поле тяготения оказывает воздействие, так как инертная и тяжелая массы эквивалентны. Луч света будет искривляться в поле тяготения точно так же, как искривляется траектория тела, брошенного горизонтально со скоростью, равной скорости света. Если бы внутренний наблюдатель рассуждал строго и принял бы во внимание искривление световых лучей в поле тяготения, то его выводы были бы точно такими же, как и выводы внешнего наблюдателя.

Поле тяготения Земли, конечно, очень слабо для того, чтобы искривление светового луча в нем можно было обнаружить непосредственно экспериментом. Но известные опыты, проделанные во время солнечных затмений, убедительно, хотя и косвенно, показывают влияние поля тяготения на путь светового луча.

Из этих примеров следует, что имеется вполне обоснованная надежда сформулировать релятивистскую физику. Но для этого мы должны сначала разрешить проблему тяготения.

Мы видели на примере с лифтом последовательность двух описаний. Можно предположить наличие неравномерности движения, а можно этого не делать. Мы можем исключить из наших примеров «абсолютное» движение с помощью поля тяготения. Но тогда в неравномерном движении нет ничего абсолютного. Поле тяготения в состоянии полностью его уничтожить.

Призраки абсолютного движения и инерциальной системы координат могут быть исключены из физики, и может быть построена новая релятивистская физика. Наши идеализированные опыты показывают, как тесно связана проблема общей теории относительности с проблемой тяготения и почему эквивалентность тяжелой и инертной масс так существенна для этой связи. Ясно, что решение проблемы тяготения в общей теории относительности должно отличаться от ньютоновского. Законы тяготения, так же как и все законы природы, должны быть сформулированы для всех возможных систем координат, в то время как законы классической механики, сформулированные Ньютоном, справедливы лишь в инерциальных системах координат.

Геометрия и опыт.

Наш следующий пример будет более фантастичным, чем пример с падающим лифтом. Мы должны подойти к новой проблеме, проблеме связи между общей теорией относительности и геометрией. Начнем с описания мира, в котором живут лишь двухмерные, а не трехмерные существа, как в нашем. Кинематограф приучил нас к двухмерным существам, действующим на двухмерном экране. Представим себе теперь, что эти теневые фигуры, действующие на экране, действительно существуют, что они обладают способностью мышления, что они могут создавать свою собственную науку, что для них двухмерный экран олицетворяет геометрическое пространство. Эти существа не в состоянии представить себе наглядным образом трехмерное пространство так же, как мы не в состоянии представить мир четырех измерений. Они могут изогнуть прямую линию; они знают, что такое круг, но они не в состоянии построить сферу, потому что это означало бы покинуть их двухмерный экран. Мы находимся в таком же положении. Мы в состоянии изогнуть и линию, и поверхности, но мы с трудом можем представить искривленное пространство.

Живя, мысля и экспериментируя, наши теневые фигуры могли бы, возможно, овладеть знанием двухмерной евклидовой геометрии. Таким образом, они могли бы доказать, что сумма углов в треугольнике равна 180 градусам. Они могли бы построить два круга с общим центром, один очень малый, а другой большой. Они нашли бы, что отношение длин окружностей двух таких кругов равно отношению их радиусов — результат, опять характерный для евклидовой геометрии. Если бы экран был бесконечно велик, то наши теневые существа нашли бы, что, отправившись однажды в путешествие вперед по прямой, они никогда не вернулись бы к своей отправной точке.

Представим себе теперь, что эти двухмерные существа живут в измененных условиях. Предположим, что кто-то извне, из «третьего измерения», перенес их с экрана на поверхность сферы с очень большим радиусом. Если эти тени очень малы по отношению ко всей поверхности, если у них нет средств дальнего сообщения и они не могут двигаться очень далеко, то они не обнаружат какого-либо изменения. Сумма углов в малых треугольниках еще составляет 180 градусов. Отношение радиусов двух малых кругов с общим центром еще равно отношению длин их окружностей.

Но пусть эти теневые существа с течением времени развивают свои теоретические и технические познания. Пусть ими найдены средства сообщения, позволяющие им быстро покрывать огромные расстояния. Тогда они найдут, что, отправляясь в путешествие прямо вперед, они, в конце концов, вернутся к своей исходной точке. «Прямо вперед» означает вдоль большого круга сферы. Они найдут также, что отношение длин двух концентрических окружностей не равно отношению радиусов, если один из радиусов мал, а другой велик.

Если наши двухмерные существа консервативны, если их поколения изучали евклидову геометрию в прошлом, когда они не могли далеко путешествовать и когда эта геометрия соответствовала наблюдаемым фактам, то они, конечно, сделают все возможное, чтобы сохранить ее, несмотря на очевидность своих измерений. Они постараются заставить физику нести бремя этих противоречий. Они станут искать какие-либо физические основания, скажем, различие температур, деформирующее линии и вызывающее отклонение от евклидовой геометрии. Но раньше или позже они должны будут найти, что имеется гораздо более логический и последовательный путь описания этих явлений. Они окончательно поймут, что их мир конечен, что его геометрические принципы отличны от тех, которые они изучали. Несмотря на свою неспособность представить себе свой мир, они поймут, что он есть двухмерная поверхность сферы. Они скоро изучат новые принципы геометрии, которая, хотя и отличается от евклидовой, тем не менее, может быть сформулирована так же последовательно и логично для их двухмерного мира. Новому поколению, воспитанному на знании сферической геометрии, старая евклидова геометрия будет казаться более сложной и искусственной, так как она не соответствует наблюдаемым фактам.

Вернемся к трехмерным существам нашего мира.

Что это значит, когда утверждают, что наше трехмерное пространство имеет евклидов характер? Смысл этого в том, что все логически доказанные положения евклидовой геометрии могут быть точно подтверждены действительным экспериментом. С помощью твердых тел или световых лучей мы можем построить объекты, соответствующие идеализированным объектам евклидовой геометрии. Ребро линейки или световой луч соответствуют прямой. Сумма углов треугольника, построенного из тонких жестких стержней, равна 180 градусам. Отношение радиусов двух концентрических окружностей, построенных из тонкой упругой проволоки, равно отношению длин окружностей. Истолкованная таким образом евклидова геометрия становится главой физики, хотя и очень простой ее главой.

Но мы можем представить себе, что обнаружены противоречия: например, что сумма углов большого треугольника, построенного из стержней, которые по многим основаниям должны были считаться твердыми, не равна 180 градусам. Так как мы уже прибегали к идее конкретного представления объектов евклидовой геометрии с помощью твердых тел, то мы, вероятно, стали бы искать какие-либо физические силы, которые явились причиной такого неожиданного поведения наших стержней. Мы постарались бы найти физическую природу этих сил и их влияние на другие явления. Чтобы спасти евклидову геометрию, мы обвинили бы объекты в том, что они не тверды, что они не точно соответствуют объектам евклидовой геометрии. Мы постарались бы найти лучшие тела, ведущие себя так, как это ожидается согласно евклидовой геометрии. Если бы, однако, нам не удалось объединить евклидову геометрию и физику в простую и последовательную картину, то мы должны были бы отказаться от идеи, что наше пространство евклидово, и искать более последовательную картину реальности на основе более общих предположений о геометрических свойствах нашего пространства.

Необходимость этого может быть проиллюстрирована с помощью идеализированного эксперимента, показывающего, что действительно релятивистская физика не может основываться на евклидовой геометрии. Наши рассуждения будут предполагать, что уже известны выводы, касающиеся инерциальной системы координат, а также специальная теория относительности.

Представим себе большой диск с двумя концентрическими окружностями, нарисованными на нем; одна из этих окружностей мала, другая очень велика (рис. 66).

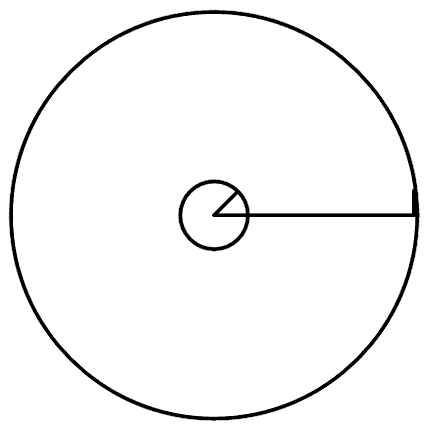
Рис. 66.

Диск быстро вращается. Он вращается относительно внешнего наблюдателя; пусть имеется еще внутренний наблюдатель, помещающийся на диске. Предположим далее, что система координат внешнего наблюдателя инерциальна. Внешний наблюдатель может нарисовать в своей инерциальной системе две такие же окружности — малую и большую, покоящиеся в его системе, но совпадающие с окружностями на вращающемся диске. Евклидова геометрия справедлива в его системе координат, так как его система инерциальна, — так что отношение длин окружностей равно отношению радиусов. А что же находит наблюдатель на диске? С точки зрения классической физики, а также специальной теории относительности его система координат недопустима. Но если мы стремимся найти новую форму физических законов, справедливую в любой системе координат, то мы должны рассматривать наблюдателя на диске и наблюдателя внешнего с одинаковой серьезностью. Теперь мы извне следим за попыткой внутреннего наблюдателя найти путем измерения длины окружностей и радиусов на вращающемся диске. Он использует такой же небольшой измерительный масштаб, какой был использован внешним наблюдателем. «Такой же» означает либо действительно тот же, просто переданный внешним наблюдателем внутреннему, либо один из двух масштабов, имеющих одинаковую длину в покоящейся системе координат.

Внутренний наблюдатель на диске начинает измерение радиуса и длины окружности малого круга. Его результат может оказаться таким же, как и результат внешнего наблюдателя. Ось, на которой вращается диск, проходит через центр. Те части диска, которые близки к центру, имеют очень небольшие скорости. Если окружность достаточно мала, мы можем спокойно применить классическую механику и не обращать внимания на специальную теорию относительности. Это означает, что отрезок имеет одинаковую длину как для внешнего, так и для внутреннего наблюдателя, и результат двух измерений будет одинаков для них обоих. Теперь наблюдатель на диске измеряет радиус большой окружности. Помещенный на радиусе отрезок движется относительно внешнего наблюдателя. Однако такой отрезок не сокращается и будет иметь одинаковую длину для обоих наблюдателей, так как направление движения перпендикулярно к отрезку. Таким образом, три измерения одинаковы для обоих наблюдателей: два радиуса и малая окружность. Но не так обстоит дело с четвертым измерением. Длина большой окружности будет различна для обоих наблюдателей. Отрезок, помещенный на окружности в направлении движения, теперь будет казаться сокращенным для внешнего наблюдателя сравнительно с соответствующим ему покоящимся отрезком. Скорость на внешней окружности гораздо больше, чем скорость на внутренней окружности, и это сокращение должно быть учтено. Поэтому, если мы применим выводы специальной теории относительности, наше заключение будет таково: длина большой окружности должна быть различной, если она измеряется обоими наблюдателями. Так как только одна из четырех длин, измеренных обоими наблюдателями, не будет одинаковой для обоих, то для внутреннего наблюдателя отношение обоих радиусов не может быть равным отношению окружностей, как это имеет место для внешнего наблюдателя. Это означает, что наблюдатель на диске не может подтвердить справедливость евклидовой геометрии в своей системе.

После получения этого результата наблюдатель на диске может сказать, что он не хочет рассматривать систему координат, в которой несправедлива евклидова геометрия. Нарушение евклидовой геометрии обязано абсолютному вращению, тому факту, что система координат, с которой связан наблюдатель, плоха и недопустима. Но, утверждая это, он отвергает важную идею общей теории относительности. С другой стороны, если мы хотим отвергнуть абсолютное движение и сохранить идею об общей относительности, то вся физика должна быть построена на основе более общей геометрии, чем евклидова. Нет возможности избежать этих следствий, если допустимы все системы координат.

Изменения, произведенные общей теорией относительности, не могут ограничиваться одним пространством. В специальной теории относительности у нас были часы, покоящиеся в каждой из систем координат, имеющие одинаковый ритм и синхронизированные, т. е. показывающие одинаковое время в один и тот же момент. Что происходит с часами в неинерциальной системе координат? Идеализированный эксперимент с диском снова будет нам полезен. Внешний наблюдатель имеет в своей инерциальной системе совершенные часы, которые все синхронизированы, все имеют одинаковый ритм. Внутренний наблюдатель берет двое часов одинакового сорта и помещает одни из них на малую внутреннюю окружность, а другие на большую внешнюю. Часы на внутренней окружности имеют очень небольшую скорость по отношению к внешнему наблюдателю. Поэтому мы можем спокойно заключить, что их ритм будет одинаков с ритмом внешних часов. Но часы на большой окружности имеют значительную скорость, изменяющую их ритм сравнительно с часами внешнего наблюдателя, а стало быть, и сравнительно с часами, помещенными на малой окружности. Таким образом, двое вращающихся часов будут иметь различный ритм, а применяя выводы специальной теории относительности, мы снова видим, что мы не можем во вращающейся системе создать какие-либо приборы, подобные приборам в инерциальной системе координат. Чтобы выяснить, какие выводы могут быть сделаны из этого и из описанных ранее идеализированных экспериментов, приведем еще раз разговор между старым физиком С, который верит в классическую физику, и современным физиком Н, который признает общую теорию относительности. Пусть С будет внешним наблюдателем в инерциальной системе координат, а Н — наблюдателем на вращающемся диске.

С. В вашей системе евклидова геометрия несправедлива. Я следил за вашими измерениями, и я согласен, что отношение двух окружностей в вашей системе не равно отношению их радиусов. Но это показывает, что ваша система координат недопустима. А моя система — инерциального характера, и я свободно могу применять евклидову геометрию. Ваш диск находится в абсолютном движении и с точки зрения классической физики образует недопустимую систему, в которой законы механики несправедливы.

Н. Я не хочу ничего слышать об абсолютном движении. Моя система так же хороша, как и ваша. Что я заметил, так это ваше вращение по отношению к моему диску. Никто не может мне запретить отнести все движения к моему диску.

С. Но не чувствовали ли вы странной силы, стремящейся удалить вас от центра диска? Если бы ваш диск не был быстро вращающейся каруселью, то две вещи, которые вы наблюдали, конечно, не имели бы места. Вы не заметили бы силы, толкающей вас к границе диска, и не заметили бы, что евклидова геометрия неприменима в вашей системе. Не достаточны ли эти факты, чтобы убедить вас, что ваша система находится в абсолютном движении?

Н. Вовсе нет! Я, конечно, заметил оба факта, упомянутые вами, но я полагаю, что оба они вызываются сильным полем тяготения, действующим на мой диск. Поле тяготения, направленное от центра диска, деформирует мои твердые тела и изменяет ритм моих часов. Поле тяготения, неевклидова геометрия, часы с различным ритмом — все это кажется мне тесно связанным. Принимая какую-либо систему координат, я должен одновременно предположить наличие соответствующего поля тяготения и его влияние на твердые тела и часы.

С. Но вы знаете о трудностях, вызванных вашей общей теорией относительности? Мне хотелось бы сделать свою точку зрения ясной, приведя простой не физический пример. Представим себе идеализированный американский город, состоящий из параллельных улиц с параллельными проспектами, расположенными перпендикулярно к ним (рис. 67).

Рис. 67.

Расстояние между улицами, а также между проспектами всюду одно и то же. Поскольку это так, то и кварталы совершенно одинаковы по величине. Таким путем я могу легко характеризовать положение любого квартала. Но это построение было бы невозможно без евклидовой геометрии. Таким образом, например, мы не можем покрыть всю нашу Землю одним большим идеальным американским городом. Один взгляд на глобус убедит вас в этом. Но мы не могли бы покрыть и ваш диск такой «американской городской конструкцией». Вы утверждаете, что ваши стержни деформированы гравитационным полем. Тот факт, что вы не могли подтвердить теорему Евклида о равенстве отношений радиусов и окружностей, ясно показывает, что если вы продолжите такое строительство улиц и проспектов достаточно далеко, то рано или поздно, вы придете к трудностям и найдете, что оно невозможно на вашем диске. Ваша геометрия на вращающемся диске подобна геометрии на кривой поверхности, где, конечно, указанное построение улиц и проспектов на достаточно большой части поверхности невозможно. Для того чтобы пример был более физическим, возьмем пластинку, неравномерно нагретую, с различной температурой в разных частях поверхности. Можете ли вы с помощью тонких железных прутов, длина которых увеличивается от нагревания, выполнить «параллельно-перпендикулярное» построение, нарисованное мною ниже? Конечно, нет! Ваше «поле тяготения» разыгрывает над вашими стержнями ту же шутку, что и изменение температуры над тонкими железными прутами.

Н. Все это не пугает меня. Построение улиц и проспектов необходимо для того, чтобы определить положения точек, часы — для того, чтобы установить порядок событий. Вовсе не необходимо, чтобы город был американским: с таким же успехом он может быть и древнеевропейским. Представим себе идеализированный город, построенный из пластичного материала и затем деформированный (рис. 68).

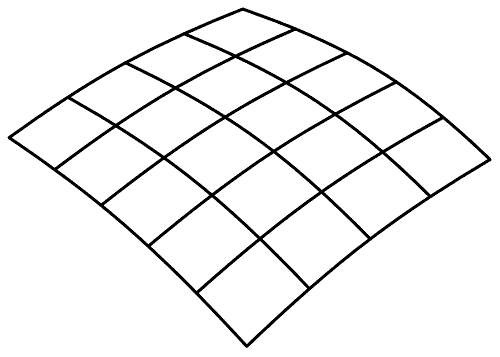
Рис. 68.

Я могу все еще подсчитать кварталы и проспекты, хотя они уже больше не прямые и не равноудалены друг от друга. Подобно этому долготы и широты отмечают положения точек на нашей Земле, хотя на ней и нельзя осуществить построения «американского города».

С. Но я вижу еще трудность. Вы вынуждены использовать вашу «европейскую городскую структуру». Я согласен, что вы можете установить порядок точек или времени событий, но это построение спутает все измерения расстояний. Оно не даст вам метрические свойства пространства, как это дает мое построение. Возьмем пример. Я знаю, что пройдя в моем американском городе десять кварталов, я дважды покрою расстояния пяти кварталов. Так как я знаю, что все кварталы равны, я сразу же могу определить расстояния.

Н. Это верно. В моей «европейской городской структуре» я не могу сразу же определить расстояния числом деформированных кварталов. Я должен знать кое-что большее; я должен знать геометрические свойства моей поверхности. Совершенно так же каждый знает, что расстояние между 0° и 10° долготы на экваторе не равно расстоянию между теми же долготами вблизи Северного полюса. Но всякий штурман знает, как оценить расстояние между двумя такими точками на нашей Земле, ибо он знает ее геометрические свойства. Он может сделать это либо путем подсчета, основываясь на знании сферической тригонометрии, либо экспериментальным путем, проводя своей корабль по обоим путям с одинаковой скоростью. В вашем случае вся проблема тривиальна, ибо все улицы и проспекты равно отстоят друг от друга. В случае нашей Земли это уже более сложно; два меридиана 0° и 10° пересекаются на земных полюсах и наиболее отдалены друг от друга на экваторе. Подобно этому, чтобы определять расстояния, я должен знать в своей «европейской городской структуре» нечто большее, чем вы в своей «американской городской структуре». Я могу получить эти дополнительные знания изучением геометрических свойств моего континуума в каждом отдельном случае.

С. Все это только показывает, к какому неудобству и сложности приводит потеря простой структуры евклидовой геометрии ради запутанных построений, которые вы обязаны употреблять. Действительно ли это необходимо?

Н. Боюсь, что да, если мы желаем применять нашу физику в любой системе координат, не прибегая к таинственной инерциальной системе. Я согласен, что мой математический аппарат гораздо сложнее вашего, но зато мои физические предположения более просты и естественны.

Дискуссия ограничивалась двухмерным континуумом. Предмет спора в общей теории относительности еще более сложен, так как там — не двухмерный, а четырехмерный пространственно-временн?й континуум. Но идеи те же, что и набросанные здесь для случая двухмерного пространства. В общей теории относительности мы не можем применять механических построений с помощью сети параллельно-перпендикулярных стержней и синхронизированных часов, как в специальной теории относительности. В произвольной системе координат мы не можем определить точку и момент времени, в которые произошло событие, используя твердые стержни и ритмичные и синхронизированные часы, как в инерциальной системе координат специальной теории относительности. Мы по-прежнему можем установить порядок событий с помощью наших неевклидовых стержней и часов с различным ритмом. Но действительные измерения, требующие твердых стержней и совершенных ритмических и синхронизированных часов, могут быть выполнены только в локальной инерциальной системе. Для такой системы справедлива вся специальная теория относительности. Но наша «хорошая» система координат только локальна, ее инерциальный характер ограничен в пространстве и времени. Даже в нашей произвольной системе координат мы можем предвидеть результаты измерений, сделанные в локальной инерциальной системе. Но для этого мы должны знать геометрический характер нашего пространственно-временн?го континуума.

Наши идеализированные эксперименты показывают только общий характер новой релятивистской физики. Эти эксперименты показывают нам, что основной проблемой является проблема тяготения. Они показывают нам также, что общая теория относительности приводит к дальнейшему обобщению понятий времени и пространства.

Общая относительность и ее экспериментальная проверка.

Общая теория относительности пытается сформулировать физические законы для всех систем координат. Фундаментальная проблема теории относительности есть проблема тяготения. Теория относительности сделала первое со времени Ньютона серьезное усилие заново сформулировать закон тяготения. Действительно ли это необходимо? Мы уже узнали о достижениях теории Ньютона, об огромном развитии астрономии, основанном на его законе тяготения. Ньютонов закон еще остается основой всех астрономических расчетов. Но мы узнали также о некоторых возражениях против старой теории. Ньютонов закон справедлив только в инерциальной системе координат классической физики, в системе координат, определенной, как мы помним, условием, что в ней должны быть справедливы законы механики. Сила, действующая между двумя массами, зависит от расстояния между ними. Связь между силой и расстоянием, как мы знаем, инвариантна относительно классических преобразований. Но этот закон не соответствует строению специальной теории относительности. Расстояние не инвариантно по отношению к преобразованиям Лоренца. Мы могли бы стараться, что мы и делали успешно в отношении законов движения, обобщить закон тяготения, сделать его соответствующим специальной теории относительности или, другими словами, сформулировать его так, чтобы он был инвариантным по отношению к преобразованиям Лоренца, а не по отношению к классическим преобразованиям. Но ньютонов закон тяготения упрямо сопротивляется всем нашим усилиям упростить и приспособить его к схеме специальной теории относительности. Даже если бы это и удалось нам, был бы необходим еще дальнейший шаг, шаг от инерциальной системы координат специальной теории относительности к произвольной системе общей теории относительности. С другой стороны, идеализированный эксперимент с падающим лифтом ясно показывает, что нет шансов сформулировать общую теорию относительности без разрешения проблемы тяготения. Из наших рассуждений видно, почему решение проблемы тяготения различно в классической физике и в общей теории относительности.

Мы постарались показать путь, ведущий нас к общей теории относительности, и основания, вынуждающие нас еще раз изменить наши старые взгляды. Не входя в формальную структуру теории, мы охарактеризуем некоторые черты новой теории тяготения для сравнения со старой. Не слишком трудно будет понять природу различий обеих теорий после всего, что было ранее сказано.

1. Гравитационные уравнения общей теории относительности могут быть применены к любой системе координат. Выбрать какую-либо особую систему координат в специальном случае — дело лишь удобства. Теоретически допустимы все системы координат. Игнорируя тяготение, мы автоматически возвращаемся к инерциальной системе специальной теории относительности.

2. Ньютонов закон тяготения связывает движение тела здесь и теперь с действием другого тела в то же самое время на далеком расстоянии. Этот закон стал образцом для всего механистического мировоззрения. Но механистическое мировоззрение потерпело крах. В уравнениях Максвелла мы создали новый образец для законов природы. Уравнения Максвелла суть структурные законы. Они связывают события, которые происходят теперь и здесь, с событиями, которые происходят немного позднее и в непосредственном соседстве. Они — суть законы, описывающие электромагнитное поле. Наши новые гравитационные уравнения суть также структурные законы, описывающие изменение поля тяготения. Схематически мы можем сказать: переход от ньютонова закона тяготения к общей относительности до некоторой степени аналогичен переходу от теории электрических жидкостей и закона Кулона к теории Максвелла.

3. Наш мир неевклидов. Геометрическая природа его образована массами и их скоростями. Гравитационные уравнения общей теории относительности стремятся раскрыть геометрические свойства нашего мира.

Предположим на минуту, что нам удалось последовательно выполнить программу общей теории относительности. Но не грозит ли нам опасность увлечения спекуляциями, слишком далекими от реальности? Мы знаем, как хорошо старая теория объясняет астрономические наблюдения. Можно ли построить мост между новой теорией и наблюдением? Каждое рассуждение должно проверяться экспериментом, и любые выводы, как бы привлекательны они ни были, должны отбрасываться, если не соответствуют фактам. Как выдержала новая теория тяготения экспериментальную проверку? Ответ на этот вопрос можно дать в следующем предложении: старая теория есть особый предельный случай новой. Если силы тяготения сравнительно слабы, прежний ньютонов закон оказывается хорошим приближением к новым законам тяготения. Таким образом, все наблюдения, подтверждающие классическую теорию, подтверждают и общую теорию относительности. Мы вновь приходим к старой теории от более высокого уровня новой.

Даже если бы нельзя было указать дополнительных наблюдений в пользу новой теории, если бы ее объяснения были лишь столь же хороши, как и объяснения старой теории, предоставляя тем самым свободный выбор между обеими теориями, мы должны были бы отдать предпочтение новой. Уравнения новой теории с формальной точки зрения сложнее, но их предпосылки с точки зрения основных принципов гораздо проще. Исчезли два страшных привидения — абсолютное время и инерциальная система. Чрезвычайно важная идея эквивалентности тяжелой и инертной масс не осталась без внимания. Не надо допущений, касающихся сил тяготения и их зависимости от расстояния. Уравнения тяготения имеют форму структурных законов, форму, которая требуется от всех физических законов со времени великих достижений теории поля.

Из новых гравитационных законов могут быть сделаны и новые выводы, не содержащиеся в законах тяготения Ньютона. Один вывод, а именно отклонение светового луча в поле тяготения, уже указывался. Приведем еще два других следствия.

Если старые законы вытекают из новых, когда силы тяготения слабы, то отклонения от ньютонова закона тяготения можно ожидать только для сравнительно больших сил тяготения. Возьмем нашу солнечную систему. Планеты, и среди них наша Земля, движутся по эллиптическим орбитам вокруг Солнца. Меркурий — планета, наиболее близкая к Солнцу. Притяжение между Солнцем и Меркурием сильнее, чем между Солнцем и любой другой планетой, так как расстояние его от Солнца меньше. Если имеется какая-либо надежда найти отклонение от закона Ньютона, то наибольший шанс — движение Меркурия. Из классической теории следует, что путь, описываемый Меркурием, того же вида, как и путь любой другой планеты, и отличается лишь тем, что он ближе к Солнцу. Согласно общей теории относительности движение должно немного отличаться. Не только Меркурий должен вращаться вокруг солнца, но и эллипс, который он описывает, должен очень медленно вращаться относительно системы координат, связанной с Солнцем (рис. 69).

Рис. 69.

Это вращение эллипса выражает новый эффект общей теории относительности. Новая теория предсказывает величину этого эффекта. Эллипс Меркурия осуществлял бы полное вращение в три миллиона лет! Мы видим, как незначителен этот эффект и как безнадежно было бы искать его в отношении планет, обращающихся на более далеком расстоянии от Солнца.

Отклонение орбиты планеты Меркурий от эллиптической было известно прежде, чем была сформулирована общая теория относительности, но никакого объяснения этому нельзя было найти. С другой стороны, общая теория относительности развивалась без всякого внимания к этой специальной проблеме. Заключение о вращении эллипса при движении планеты вокруг Солнца было сделано позднее из новых гравитационных уравнений. Теория успешно объяснила отклонение действительно происходящего движения Меркурия от движения, предписываемого законом Ньютона.

Но существует еще одно заключение, которое было сделано из общей теории относительности и сравнено с опытом. Мы уже видели, что ритм часов, помещенных на большой окружности вращающегося диска, отличен от ритма часов, помещенных на меньшем круге. Аналогично из теории относительности следует, что ритм часов, помещенных на Солнце, отличался бы от ритма часов, помещенных на Земле, так как влияние поля тяготения гораздо сильнее на Солнце, чем на Земле.

Мы заметили, что натрий, когда он раскален, испускает однородный желтый свет определенной длины волны. В этом излучении атом обнаруживает один из своих ритмов; атом представляет собой, так сказать, часы, а излученная длина волны — один из его ритмов. Согласно общей теории относительности длина волны света, излученного атомом натрия, скажем, помещенного на Солнце, должна быть несколько больше, чем длина волны света, излученного атомом натрия на нашей Земле.

Проблема проверки следствий общей теории относительности путем наблюдений сложна и точно никоим образом не решена. Поскольку мы интересуемся принципиальными идеями, мы не хотим входить в этот предмет глубже, а только устанавливаем, что пока приговор эксперимента, по-видимому, таков: подтвердить выводы, сделанные из общей теории относительности.

Поле и вещество.

Мы видели, как и почему механистическая точка зрения потерпела крах. Невозможно было объяснить все явления, предполагая, что между неизменными частицами действуют простые силы. Первые попытки отойти от механистического взгляда и ввести понятия поля оказались наиболее успешными в области электромагнитных явлений. Были сформулированы структурные законы для электромагнитного поля — законы, связывающие события, смежные в пространстве и во времени. Эти законы соответствуют характеру специальной теории относительности, так как они инварианты по отношению к преобразованиям Лоренца. Позднее общая теория относительности сформулировала законы тяготения. Они опять-таки являются структурными законами, описывающими поле тяготения между материальными частицами. Точно так же легко было обобщать уравнения Максвелла так, чтобы их можно было применить в любой системе координат, аналогично законам тяготения общей теории относительности.

Мы имеем две реальности: вещество и поле. Несомненно, что в настоящее время мы не можем представить себе всю физику построенной на понятии вещества, как это делали физики в начале девятнадцатого столетия. В настоящее время мы принимаем оба понятия. Можем ли мы считать вещество и поле двумя различными, несходными реальностями? Пусть дана маленькая частица вещества; мы могли бы наивно представить себе, что имеется определенная поверхность частицы, за пределами которой ее уже нет, а появляется ее поле тяготения. В нашей картине область, в которой справедливы законы поля, резко отделена от области, в которой находится вещество. Но что является физическим критерием, различающим вещество и поле? Раньше, когда мы не знали теории относительности, мы пытались бы ответить на этот вопрос следующим образом: вещество имеет массу, в то время как поле ее не имеет. Поле представляет энергию, вещество представляет массу. Но мы уже знаем, что такой ответ в свете новых знаний недостаточен. Из теории относительности мы знаем, что вещество представляет собой огромные запасы энергии и что энергия представляет вещество. Мы не можем таким путем провести качественное различие между веществом и полем, так как различие между массой и энергией не качественное. Гораздо большая часть энергии сосредоточена в веществе, но поле, окружающее частицу, также представляет собой энергию, хотя и в несравненно меньшем количестве. Поэтому мы могли бы сказать: вещество — там, где концентрация энергии велика, поле — там, где концентрация энергии мала. Но если это так, то различие между веществом и полем скорее количественное, чем качественное. Нет смысла рассматривать вещество и поле как два качества, совершенно отличные друг от друга. Мы не можем представить себе определенную поверхность, ясно разделяющую поле и вещество.

Те же трудности вырастают для заряда и его поля. Кажется невозможным дать ясный качественный критерий для различения между веществом и полем или зарядом и полем.

Структурные законы, то есть законы Максвелла и гравитационные законы, нарушаются для очень большой концентрации энергии или, как мы можем сказать, они нарушаются там, где присутствуют источники поля, т. е. электрические заряды или вещество. Но не можем ли мы слегка модифицировать наши уравнения так, чтобы они были справедливы всюду, даже в областях, где энергия колоссально сконцентрирована?

Мы не можем построить физику на основе только одного понятия — вещества. Но деление на вещество и поле, после признания эквивалентности массы и энергии, есть нечто искусственное и неясно определенное. Не можем ли мы отказаться от понятия вещества и построить чистую физику поля? То, что действует на наши чувства в виде вещества, есть на деле огромная концентрация энергии в сравнительно малом пространстве. Мы могли бы рассматривать вещество как такие области в пространстве, где поле чрезвычайно сильно. Таким путем можно было бы создать основы новой философии. Ее конечная цель состояла бы в объяснении всех событий в природе структурными законами, справедливыми всегда и всюду. С этой точки зрения брошенный камень есть изменяющееся поле, в котором состояния наибольшей интенсивности поля перемещаются в пространстве со скоростью камня. В нашей новой физике не было бы места и для поля, и для вещества, поскольку единственной реальностью было бы поле. Этот новый взгляд внушен огромными достижениями физики поля, успехом в выражении законов электричества, магнетизма, тяготения в форме структурных законов и, наконец, эквивалентностью массы и энергии. Нашей основной задачей было бы модифицировать законы поля таким образом, чтобы они не нарушались для областей, в которых энергия имеет колоссальную концентрацию.

Но до сих пор мы не имели успеха в последовательном и убедительном выполнении этой программы. Заключение о том, возможно ли ее выполнить, — принадлежит будущему. В настоящее время во всех наших реальных теоретических построениях мы все еще должны допускать две реальности — поле и вещество.

Фундаментальные проблемы еще стоят перед нами. Мы знаем, что все вещество состоит лишь из частиц немногих видов. Как различные формы вещества построены на этих элементарных частицах? Как эти элементарные частицы взаимодействуют с полем? Поиски ответа на эти вопросы привели к новым идеям в физике, идеям квантовой теории.

Подведем итоги:

В физике появилось новое понятие, самое важное достижение со времени Ньютона: поле. Потребовалось большое научное воображение, чтобы уяснить себе, что не заряды и не частицы, а поле в пространстве между зарядами и частицами существенно для описания физических явлений. Понятие поля оказывается весьма удачным и приводит к формулированию уравнений Максвелла, описывающих структуру электромагнитного поля, управляющих электрическими, равно как и оптическими явлениями.

Теория относительности возникает из проблемы поля. Противоречия и непоследовательность старых теорий вынуждают нас приписывать новые свойства пространственно-временн?му континууму, этой арене, на которой разыгрываются все события нашего физического мира.

Теория относительности развивается двумя этапами. Первый этап приводит к так называемой специальной теории относительности, применяемой только к инерциальным системам координат, т. е. к системам, в которых справедлив закон инерции, как он был сформулирован Ньютоном. Специальная теория относительности основывается на двух фундаментальных положениях: физические законы одинаковы во всех системах координат, движущихся прямолинейно и равномерно друг относительно друга; скорость света всегда имеет одно и то же значение. Из этих положений, полностью подтвержденных экспериментом, выведены свойства движущихся стержней и часов, изменения их длины и ритма, зависящие от скорости. Теория относительности изменяет законы механики. Старые законы несправедливы, если скорость движущейся частицы приближается к скорости света. Новые законы движения тела, сформулированные теорией относительности, блестяще подтверждаются экспериментом. Дальнейшее следствие теории относительности (специальной) есть связь между массой и энергией. Масса — это энергия, а энергия имеет массу. Оба закона сохранения — закон сохранения массы и закон сохранения энергии — объединяются теорией относительности в один закон, в закон сохранения массы-энергии.

Общая теория относительности дает еще более глубокий анализ пространственно-временн?го континуума. Справедливость теории относительности больше не ограничивается инерциальными системами координат. Теория берется за проблему тяготения и формулирует новые структурные законы для поля тяготения. Она заставляет нас проанализировать роль, которую играет геометрия в описании физического мира. Эквивалентность тяжелой и инертной масс она рассматривает как существенный, а не просто случайный факт, каким она была в классической механике. Экспериментальные следствия общей теории относительности лишь слегка отличаются от следствий классической механики. Они выдерживают экспериментальную проверку всюду, где возможно сравнение. Но сила теории заключается в ее внутренней согласованности и простоте ее основных положений.

Теория относительности подчеркивает важность понятия поля в физике. Но нам еще не удалось сформулировать чистую физику поля. В настоящее время мы должны еще предполагать существование и поля, и вещества.

Эйнштейн А., Инфельд Л.

Эволюция физики: Развитие идей от первоначальных понятий до теории относительности. — М., 1965. — с. 147–203.