Эволюция человеческого общества как сложной системы: глобальный тренд и циклы развития

Е. Д. Куретова

Е. С. Куркина

В этой главе проводится сравнительный анализ эволюции сложных систем. Выделены и сформулированы общие законы пространственно-временного развития. Отмечено, что эволюция сложных систем имеет циклический характер и проходит стадии подъема, ускоренного развития и стадии замедления развития, упадка и кризиса. В период кризиса появляются, начинают развиваться и распространяться новые лидеры эволюции, их может быть несколько, в конкурентной борьбе происходит отбор наиболее эффективного лидера. В процессе становления нового лидера возникают новые сети (экологические, экономические и др. цепочки), система перестраивается структурно и функционально и переходит на более высокий уровень сложности. Сложность возрастает ступенчато, скачками. Высота ступеней в процессе эволюции увеличивается, а ширина (длительность цикла) сокращается; образующаяся «лестница сложности» заканчивается точкой сингулярности – глобальной бифуркацией после которой или система погибает, или переходит в качественно новое состояние. Обновленная система начинает развиваться также циклически. Циклы развития подсистем вложены друг в друга, они образуют фрактальную структуру.

Ключевые слова: сложные системы, самоорганизация и эволюция, пространственно-временное развитие; циклы, ступени сложности, волны инноваций

Введение

Еще в 60-х годах XX века в научной среде сформировалось новое междисциплинарное движение – синергетика, или теория сложных систем. Ее становление и развитие связано с именами А. Тьюринга, И. Пригожина, Г. Хакена, С. П. Курдюмова и других ученых. Сложные системы можно кратко охарактеризовать как системы, способные к самоорганизации и эволюции. Они могут иметь самую различную природу – к сложным системам можно отнести живую клетку, человека, отдельно взятое производство, экономику государства и так далее. Однако все сложные системы имеют некоторые общие принципы построения и подчиняются единым законам развития. Синергетика ставит своей целью выявление таких базовых для всех сложных систем принципов существования и эволюции, построение универсального системного подхода к исследованию природы и общества.

Результаты многочисленных исследований динамического развития систем самой различной природы позволяют выделить некоторые основные законы эволюции, присущие всем сложным системам:

• В процессе эволюции происходит последовательное усложнение структуры и организации системы, усложнение взаимодействий внутри нее и с окружающим миром.

• Вся структурная и функциональная сложность возникает в результате процессов конкуренции среди элементов системы, находящихся на одном уровне развития.

• Развитие любой сложной системы имеет циклический характер. Периоды бурного развития чередуются с периодами спада, кризиса.

• Циклы эволюции имеют инновационную природу. Инновации зарождаются в системе в периоды кризиса, в поисках выхода из кризиса. На очередном витке эволюционной спирали появляются новые лидеры, новые более сложные организационные и функциональные структуры.

• Процесс эволюции протекает в режиме с обострением и характеризуется сжатием временных масштабов. Последовательность циклов сокращается во времени по закону геометрической прогрессии и имеет точку сгущения.

• В процессе эволюции возрастает пространственная неоднородность, усиливаются процессы концентрации, сжатие пространственных масштабов; происходит все большее расслоение, отставание и постепенное выпадение из развития наиболее отсталых структур.

• Значительные этапы эволюции заканчиваются критическими точками, прохождение которых означает вступление системы в качественно новую фазу.

Одним из основных инструментов синергетики является аппарат математического моделирования. Результаты математического моделирования в разных областях позволяют выявить общие закономерности эволюции и самоорганизации в открытых нелинейных системах. Построение и использование математических моделей придает объективность проводимым исследованиям и помогает выявить механизмы того или иного явления.

Огромный шаг в разработке синергетического подхода к математическому моделированию, к изучению сложных нелинейных систем был сделан в свое время С. П. Курдюмовым и развит его последователями и учениками. В качестве базовой модели было предложено нелинейное уравнение теплопроводности. Многолетние исследования решений этого уравнения, развивающихся

в режиме с обострением, анализ механизмов формирования и развития диссипативных структур в плазме позволили ввести несколько основополагающих понятий, применимых к анализу эволюционных процессов в самых разных областях. Во-первых, было введено понятие собственных функций нелинейной среды – строго определенного, дискретного набора пространственно-временных структур, которые могут формироваться и развиваться в данной нелинейной среде. Во-вторых, это понятие темпомира структуры, связывающего время существования структуры со скоростью (темпом) ее развития. В-третьих, это принцип объединения простых структур разного «возраста» в единую сложную структуру. В-четвертых, это идея немонотонного циклического развития как необходимого механизма поддержания «жизни» сложных структур.

С помощью таких моделей можно описать процессы эволюции в сложных системах самой различной природы. Это автокаталитические реакции в химии, взрывные режимы в физике, рыночные механизмы в экономике, информационные процессы в обществе, в том числе в глобальной системе человеческого общества. Во всех этих системах при определенных условиях происходит формирование пространственных структур разной сложности и развитие их в режиме с обострением.

В данной работе в качестве примера эволюции сложной системы рассматривается глобальная эволюция человеческого общества, или Мир-Системы. С позиции синергетики человеческое общество также представляет собой одну из сложных саморазвивающихся систем, а значит, эволюции человеческого общества присущи все перечисленные выше закономерности развития. Она имеет много общего и с эволюцией нашей Вселенной, начавшей существование с Большого Взрыва, и с химической эволюцией, приведшей к возникновению органических веществ, и с биологической эволюцией, ведущей к формированию все более сложноорганизованных популяций.

Как и у всех сложных систем, поведение Мир-Системы слабо предсказуемо, а законы эволюции общества носят характер тенденций или принципов, т. е. они выполняются с большой вероятностью, но не всегда. Тем не менее, анализ эволюции общества с позиции теории сложных систем является очень полезным и позволяет дать объективную оценку поворотного момента истории, в котором мы сейчас находимся, и наметить наиболее вероятные пути дальнейшего развития.

1. Параметры порядка Мир-Системы

Системный подход к исследованию эволюции человеческого общества предполагает рассмотрение всего человечества как единой самоорганизующейся и саморазвивающейся сложной системы. Синергетика рассматривает всю историю мирового сообщества в целом, а не как множество отдельно взятых исторических событий, имеющих место в рамках развития отдельных народов и государств. Очевидно, что все исторические события представляют собой весьма сложную взаимосвязь экономических, политических, социальных процессов, зачастую осложненных влиянием множества случайных факторов, стихийными бедствиями и катастрофами и т. д. Однако, несмотря на кажущуюся разобщенность и многообразие протекающих в мире исторических процессов, с помощью методов синергетики стало возможным проследить общие для всего человечества глобальные тенденции и закономерности развития.

Развитие синергетического подхода к исследованию истории связано, в первую очередь, с именами таких историков и социологов, как Ф. Бродель, А. Франк, И. Валлерстайн, этот подход продолжает развиваться в работах С. И. Гринина, А. В. Коротаева, С. Ю. Малкова, А. П. Назаретяна и др.[426].

Считается, что человечество, в виде первобытного общества, сформировалось в Африке примерно 1.5 млн. лет тому назад. Затем люди постепенно расселились по всей планете, заняв все более или менее пригодные для проживания места. Древний человек был частью экосистемы и отличался от других стайных хищников разве что умением добывать огонь и использовать примитивные орудия труда. Качественный скачок произошел лишь в эпоху неолита, начало которого относят к XI тысячелетию до н. э., когда человек из охотника и собирателя превратился в скотовода и земледельца и начал вести оседлый образ жизни. Эти изменения в человеческом сообществе имели настолько глобальные последствия, что были названы историками неолитической революцией. Неолитическая революция – это первая критическая точка (глобальная бифуркация) в истории развития человечества. Именно в неолите начинается формирование Мир-Системы. К концу S тыс. до н. э. жизнедеятельность основной части населения мира была основана на сельском хозяйстве. К этому времени народы, составляющие Мир-Систему, несмотря на кажущуюся разобщенность и независимость существования, находились на сходном уровне развития и взаимодействовали друг с другом, постепенно перенимая друг у друга новшества, знания, умения и технологии. Именно накопление информации, ее приумножение от поколения к поколению и распространение по всей территории обитания связывает человечество воедино, дает возможность рассматривать многообразие народов и сообществ как единую целостную систему[427].

Эволюция Мир-Системы, как и эволюция любой сложной системы, сопровождалась усложнением взаимодействий внутри нее и с окружающим миром. Сложность возрастала по всем направлениям человеческой деятельности: и в области взаимоотношений между отдельными людьми, поселениями, государствами, и в области создания новых технологий, и по линии культуры. В ходе эволюции многократно увеличилось число связей, намного усложнилась архитектура социально-экономического устройства общества.

С точки зрения математического моделирования, для того, чтобы говорить об усложнении структуры и организации системы, необходимо выявить те немногие параметры, которые характеризуют ее динамику и по которым можно наиболее объективно судить об увеличении структурной и функциональной сложности. Такие величины называют параметрами порядка – это те главные медленно меняющиеся переменные, описывающие изучаемый процесс развития, под которые подстраиваются все другие переменные. Только определив параметры порядка социально-экономического развития общества, можно создавать относительно простые математические модели эволюции Мир-Системы, которые позволяют анализировать ход событий, наблюдаемых в прошлом и в настоящем, и строить вероятные сценарии их развития в будущем.

Для человеческого сообщества сложность отражается, например, в уровне развития технологий. Под уровнем развития технологий (Р) понимаются не только основные технологии жизнеобеспечения, но и социально-экономическую организацию общества, уровень развития медицины, культуры, науки. Очевидно, что переход Мир-Системы на более высокий уровень сложности сопровождается увеличением этого показателя. Это всегда связано с появлением крупных инноваций – фундаментальных открытий, позволяющих овладеть новыми ресурсами и возможностями, и становящимися новыми образцами технологического, социального или культурного развития. С уровнем развития технологий связан, прежде всего, такой глобальный показатель развития системы как общая численность людей N. Это еще один параметр, характеризующий уровень развития человеческого общества в целом.

N и Р – это два главных параметра порядка развития человеческой цивилизации. Они взаимосвязаны между собой: чем выше уровень развития технологий Р, тем больше емкость социальноэкономической среды (экологической ниши) и больше людей N может существовать; в свою очередь, чем больше N, тем выше вероятность создания новых, более эффективных технологий, создающих более широкие условия проживания и способных в конечном итоге сохранить большее количество жизней. Таким образом, существует положительная обратная связь между общей численностью людей N и уровнем развития технологий Р. Эту гипотезу высказывали в той или иной форме многие исследователи, начиная с Т. Мальтуса (С. Кузнец, М. Кремер, А. В. Подлазов, А. В. Коротаев и др.)[428]. Некоторые ученые отдавали первенство технологическому фактору (М. Кремер), другие – демографическому (С. П. Капица).

С учетом вышесказанного, в дальнейшем будем анализировать основные принципы эволюции человеческого сообщества с точки зрения динамики двух этих параметров в ходе истории.

2. Гиперболический рост населения как основной тренд развития Мир-Системы

Благодаря положительной обратной связи между Р и А/, в ходе эволюции наблюдался необычный для биологических популяций рост общей численности людей. На сегодняшний день численность людей на 5 порядков больше, чем численность сравнимых с нами по размеру млекопитающих. В 1960 г. группа фон Форстера собрала и обработала исторические данные и исследовала рост населения Земли почти на протяжении всей истории. Полученный закон роста удивил многих ученых, так как противоречил биологическому закону развития. Как известно, большинство биологических популяций подчиняется закону логистического роста, при котором сначала численность популяции растет экспоненциально, а затем стабилизируется на некотором уровне, определяемом ограниченными ресурсами среды обитания. Оказалось, что общая численность людей росла по гиперболическому закону, т. е. в режиме с обострением, при котором численность населения и скорость ее роста все время нарастают, и N уходит в бесконечность при стремлении времени к моменту обострения, (см. рис. 1).

Как видно из рисунка, развитие в режиме с обострением можно условно разделить на три стадии: квазистационарную стадию -1, или стадию медленного роста, когда прирост функции заметен только на очень больших промежутках времени; стадию быстрого роста – 2, и стадию взрывного развития – 3. То есть развитие в таком режиме идет с ускорением, длится конечное время и всегда заканчивается взрывом, коллапсом вблизи точки сингулярности. В реальности вблизи момента обострения система переживает сильнейший кризис, сопровождающийся качественными изменениями, и начинается новый цикл развития обновленной системы.

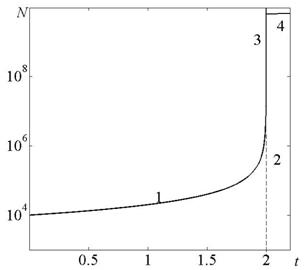
Рис. 1. Режим с обострением

В Мир-Системе закон гиперболического роста как основной тренд действовал на протяжении всей истории человечества, по некоторым оценкам более млн. лет, вплоть до 70-х годов прошлого века[429]. На квазистационарной стадии развития прирост населения был крайне мал, «спрятан» за большими флуктуациями и заметен только на больших промежутках времени. В эпоху неолита произошел переход к ускоренному росту. В последние двести лет, которые соответствуют фазе взрывного развития, наблюдалось особенно резкое увеличение численности населения Земли, которое было охарактеризовано как демографический взрыв. Население планеты в 1800 году не достигало еще 1 млрд, человек, к 1900 году уже выросло до 1650 млн., к началу 2000 г. – до 6 млрд. Сейчас численность населения Земли составляет более 7 млрд. Однако, это в примерно в два раза меньше того, что могло бы быть, если бы закон (1) продолжал бы действовать. Реальные данные начали отставать от функции (1), начиная с 70-х годов XX века. В настоящее время наблюдается резкое снижение темпов роста населения с тенденцией к стабилизации (стадия 4 на рис. 1), то, что получило название глобального демографического перехода. Демографический переход-это вторая глобальная бифуркация в истории человечества, коренным образом меняющая характер развития человечества[430].

Как уже было отмечено, развитие в режиме с обострением является характерной чертой эволюции любой сложной системы. Для сравнения приведем пример из другой предметной области, а именно, из области биоэволюции. Параметром порядка здесь может служить число типов клеток в организме. Увеличение сложности в биосфере проявляется в возникновении все более сложных живых организмов. Совершенство организма – это способность выживать и легко адаптироваться в новых условиях внешней среды. Появление более сложного организма связано с наращиванием числа типов клеток, поскольку, чем больше типов клеток в организме, тем более совершенный механизм адаптации имеет этот организм в изменяющихся внешних условиях с течением времени. Условно схема развития биосферы выглядит так: Прокариоты ? Эукариоты ? Низшие многоклеточные ? Головоногие моллюски ? Позвоночные высшие многоклеточные ? Хладнокровные ? Теплокровные ? Млекопитающие ? Приматы ? Человек. Если представить процесс усложнения как зависимость числа типов клеток различных видов организмов от времени возникновения конкретного вида, получится последовательность, показывающая ход эволюции биосферы по мере усложнения организмов. Аппроксимируя эту последовательность кривой, мы получим гиперболическую функцию. Это позволяет говорить об эволюции Биосферы как об ускоряющемся процессе, который отвечает режимам с обострением. Таким образом, перед нами предстает картина дискретной и ускоряющейся по времени биологической эволюции.

Другим примером может служить современная Вселенная – это огромная сверхсложная система с многоуровневой структурой

соподчиненных подсистем. Тенденция усложнения прослеживается здесь как в элементном составе, так и в появлении структур (от звезд до сверхскоплений галактик). Эволюцию космической материи можно изобразить в виде следующей упрощенной схемы: Нуклон ? Атомное ядро (система нуклонов) ? Атом ? Молекула (система атомов) ? Клетка (система молекул) ? Кристалл (система атомов и молекул) ? Порода (система кристаллов) ? планетарное тело (система пород) ? Солнечная система (система планетарных тел) ? Звезда ? Галактика (система звезд) ? Вселенная (суперсистема скоплений галактик). Если построить график в координатах время возникновения систем и сложность системы (условный параметр, имеющий смысл величины информации), то получится дискретная последовательность, переходы в которой ступенчаты. Аппроксимируя её, получим плавную кривую, отвечающую опять же степенной закономерности.

3. Исторические и социально-экономические циклы

Изучение исторической динамики показывает, что развитие человеческой цивилизации в режиме с обострением описывает лишь основной тренд, тогда как более детальное рассмотрение обнаруживает существование исторических циклов, или волн разной длины. Наиболее известными являются вековые циклы, продолжающиеся примерно 200–300 лет, и длинные цивилизационные волны, длительность которых составляет несколько тысяч лет[431]. Глобальные длинные волны исторического развития общества изучали И. М. Дьяконов, Ф. Бродель, С. П. Капица, П. В. Турчин и др. Разные ученые по-разному выделяют главные эпохи развития Мир-Системы, но все они отмечают ускорение течения исторического времени и сокращение длительности исторических эпох[432]. Ускорение течения исторического времени, сокращение длительности циклов дают представление об эволюции как о развитии по спирали.

Дьяконов в своей книге «Пути истории» вводит 8 фаз исторического развития, начиная с появления Homo sapiens[433]. Он замечает, что длительность циклов сокращается по закону геометрической прогрессии и имеет точку сгущения, впоследствии получившую название сингулярности Дьяконова. Ю. В. Яковец, используя понятие социально-экономической формации, данное К. Марксом, делит эволюцию общества на 9 этапов[434]. Каждый новый этап эволюции – это следующая ступень сложности организации человеческого общества. Его деление на этапы несколько отличается от деления Дьяконова, но длительность циклов также экспоненциально сокращается. С. П. Капица, как и многие другие историки, выделяет 11 глобальных исторических циклов. Провозглашая принцип демографического императива, он тесно связывает исторические циклы с ростом населения N в режиме с обострением (1). По мнению Капицы, смена эпох происходила, когда численность населения примерно утраивалась, а длительность эпох при этом сокращалась также примерно в три раза. Предельная точка сгущения циклов по Капице приходится, как и у Дьяконова, на 2022 г., и совпадает с точностью до допустимой погрешности с точкой сингулярности Форстера – 2025 г.

Очевидно, что глобальные исторические циклы не могут иметь длительность порядка часа, месяца или года. Необходимо достаточно длительное время на разработку, распространение и внедрение инноваций, определяющих целую эпоху. Минимальный период цикла предположительно составляет несколько десятилетий (сорок – сорок пять лет, или время поколения, одно из понятий, введенных С. П. Капицей). Отсюда следует, что при приближении к критической точке (точке сингулярности) исторические циклы прекращают сокращаться, останавливаясь на некотором минимальном периоде. Это еще один признак того, что демографический переход является переходом к цивилизации с другими законами и циклами развития.

Развитие человеческой цивилизации имеет выраженный циклический характер не только по времени, но и по пространству. На восходящей фазе эволюции, фазе бурного развития, преобладают центростремительные тенденции, сопровождающиеся усилением процессов концентрации в немногих центральных местах[435]. Центральные места человеческой деятельности, представляющие собой культурные, научные, технологические и другие центры, различаются по размерам, мощности и значению, и имеют ярко выраженное иерархическое строение. Именно там концентрируется население, зарождаются новые технологии, новые социальные, экономические, политические, культурные и другие стандарты. Центростремительные процессы приводят к усилению процессов концентрации и неравномерности пространственного развития, все большему расслоению системы на структуры, существующие на разных уровнях развития. Затем следует нисходящая фаза, на которой преобладают центробежные процессы, когда играет роль так называемая диффузия нововведений или диффузия инноваций. Передовые идеи, новые стандарты, новые модели взаимоотношений, возникнув первоначально в одном центре, затем «расходятся» по большей или меньшей территории и постепенно осваиваются все меньшими центрами. Говорят, что центральные места человеческой деятельности являются генераторами зонноволновой диффузии инноваций и излучают импульсы развития. Причем, чем сильнее пространственная концентрация, тем быстрее исчезают породившие ее различия между центром и периферией, тем быстрее выравниваются уровни их развития. Таким образом, диффузия инноваций играет существенную роль в цикле, определяя его длительность по времени.

Для того, чтобы исследовать свойства и механизмы формирования глобальных исторических циклов, были построены и исследованы некоторые пространственно-распределенные математические модели эволюции Мир-Системы[436]. Проанализируем ход циклического развития, используя для наглядности результаты модельных расчетов[437].

В качестве базовой модели послужило нелинейное уравнение теплопроводности, решения которого при определенных условиях развиваются в режиме с обострением. С помощью этого уравнения описывалось изменение плотности населения по времени и по пространству. Решения этого уравнения при выбранных значениях параметров представляют собой пространственную структуру с некоторой эффективной шириной, с одним максимумом в центре и постепенно уменьшающимися значениями по мере удаления от центра, показывающую распределение населения по пространству. Здесь необходимо пояснить, что при построении модели не ставилась цель отразить реальную географию земли и распределение по ее континентам народов и государств. Вместо этого рассматривалось некоторое обобщенное системное пространство. Всю совокупность центральных мест Мир-Системы, являющихся средоточием максимального развития и передовых технологий, будем представлять как единый Центр развития цивилизации. Как известно, на протяжении всей истории вплоть до второй половины XX века такая совокупность центральных мест приходилась на густонаселенные районы.

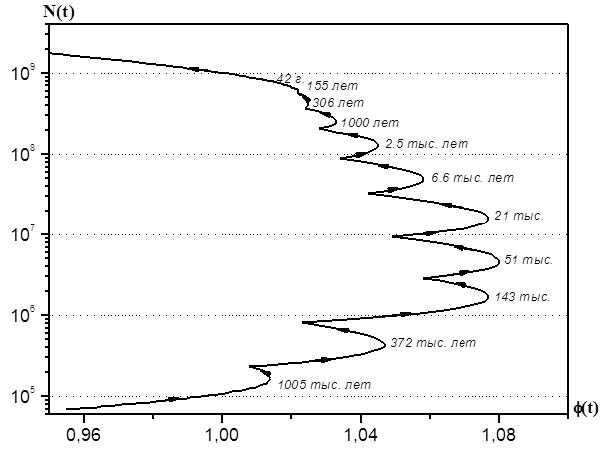
1 = 30 000 км

Рис. 2. Глобальные исторические циклы на фазовой плоскости

Поэтому центр структуры с максимальным значением плотности населения отвечает по смыслу такому виртуальному Центру Мир-Системы. Чем ниже уровень развития, чем дальше по развитию от центральных мест отстояли районы, тем меньшей плотностью населения они обладали. Это показывает, что удаление от центра структуры, сопровождаемое уменьшением плотности населения, означает удаление от Центра Мир-Системы к столь же виртуальной Периферии. То есть каждая точка нашего виртуального системного пространства соответствует совокупности мест обитания людей (народов, городов, и т. д.), находящихся на сходном уровне развития. Таким образом, отслеживая динамику развития структуры в модели, можно делать выводы об основных закономерностях пространственно-временного развития Мир-Системы.

На рис. 2 приведен результат расчетов, наглядно демонстрирующий наличие пространственно-временных циклов в системе. На рисунке изображен фазовый портрет системы, на котором показано изменение амплитуды структуры (т. е. численности населения N(t)) от ширины структуры).

За основу бралась периодизация С. П. Капицы, включающая в себя 11 исторических эпох. Продолжительность каждого витка траектории в модели согласуется с длительностью основных исторических эпох[438] и общей численностью людей на каждом этапе.

Каждый цикл можно условно разделить на две стадии: стадию «растекания», сопровождающуюся увеличением ширины структуры, и стадию быстрого роста численности, идущую с сокращением эффективной ширины. Рассмотрим первую стадию. Она описывает состояние Мир-Системы после кризиса, когда развитые цивилизации, составляющие ее Центр, находятся в состоянии упадка. Население начинает переселяться из центра на периферию в поисках новых мест работы, новых сфер влияния, более благоприятных мест проживания. На этой стадии в системе преобладают диффузионные и центробежные процессы. В модели структура начинает «растекаться» по пространству; в центре плотность перестает расти, а иногда сначала даже падает, а на периферии она, наоборот, растет быстрее. Вместе с тем, переселяясь на периферию, люди несут с собой знания, умения, технологические новшества. Новые технологии и культурные стандарты, образцы нового социального устройства медленно распространяются от центральных мест по территории, адаптируясь к новым условиям. Благодаря этому, кризис постепенно преодолевается, открываются новые возможности для роста и развития. В модели прекращается расширение структуры, траектория на фазовом портрете совершает поворот. Мир-Система переходит ко второй стадии развития, когда закрепившиеся инновации способствуют процветанию Системы и приводят к ускоренному росту численности населения. Постепенно происходит все большая концентрация населения в центре, где начинается интенсивное развитие технологий, экономики, культуры, образования и так далее; это, в свою очередь, влечет за собой все большую потребность в новых товарах, услугах, все большую конкуренцию зарождающихся новых технологий. Теперь в динамике системы преобладают центростремительные процессы, происходит все более быстрый рост в центре и отставание, постепенное «выпадение из развития» периферийных областей. В модели эта развитая стадия режима с обострением сопровождается сокращением ширины структуры и быстрым ростом численности в центре структуры. Усиливается неравномерность развития; идет процесс все большего расслоения населения по уровню развития. Начинаются кризисы перенаселенности в центральных местах, которые могут сопровождаться восстаниями, бунтами или войнами. Начинается поиск выхода из кризиса. Именно в это время рождаются глобальные инновации – образцы качественно новых технологий, новой социально-экономической организации общества, способные перевести Мир-Систему на другой, более высокий уровень развития и определяющие начало новой эпохи. Когда вся Система переживает кризис, когда расшатываются и начинает разрушаться мощно развитый центр структуры, происходит качественный эволюционный скачок. Благодаря инновациям происходит переход к новому витку эволюции, к началу нового исторического цикла. В модели траектория начинает новый виток на фазовом портрете.

Кроме того, можно заметить, что фазовый портрет имеет иерархическую структуру. Все описанные исторические циклы ложатся на глобальный цикл: как видно из рисунка, сначала происходит смещение петель вправо, то есть идет глобальное растекание по пространству, затем начинается рост общей численности, сопровождающийся общим уменьшением эффективной ширины, т. е. общей тенденцией к концентрации, сжатию пространственных масштабов. Глобальное растекание соответствует временам «охотников и собирателей». На этом этапе в динамике господствует тенденция к постоянному расселению, перемещению людей, которое вызвано истощением природных ресурсов в данной местности. На Рис. 1 это квазистационарная стадия развития -1. Она и включает в себя несколько первых самых длинных эпох и продолжается вплоть до неолита. Неолитическая революция является поворотным событием в истории человечества, когда древний человек превращается в скотовода и земледельца и начинает вести оседлый образ жизни.

В модели происходит переход от квазистационарной стадии развития к стадии быстрого роста – 2. (Рис. 1). Для этого периода характерно формирование структур (княжеств, городов, государств, империй и т. д.) на разных пространственных масштабах, образование устойчивых системных взаимосвязей. На фазовом портрете происходит постепенное глобальное сокращение ширины области распределения и опережающий рост плотности в центральной части. Дальнейшее развитие, вплоть до демографического перехода, соответствует стадии взрывного развития – 3. В целом она сопровождается быстрым сокращением пространственных и временных масштабов и сильной неустойчивостью. Усиливается неравномерность пространственного распределения, происходит все большее скопление людей в городах. На фазовой портрете модели происходит все большее сжатие циклов и по времени, и по пространству, они практически сливаются в ходе общего взрывного роста, (см. Рис. 4). Это означает, что все меньшее количество стран и людей принимают участие в общей эволюции, наблюдается «выпадение» отдельных племен и народов из развития. По мере приближения к моменту обострения, развитие Мир-Системы становится все более неустойчивым и сопровождается целым рядом негативных процессов, ведущих к разрушению целостности системы. Одновременно внутри системы вырабатываются силы, препятствующие ее саморазрушению и стремящиеся перевести ее в качественно другое состояние. В настоящее время происходит бифуркация смены режимов цивилизационного развития, или демографический переход. Период исторических циклов достигает своего минимума, равного 40–45 годам и определяемого так называемым временем поколения[439], и на этом стабилизируется. Исторические циклы, по-видимому, сливаются с глобальными экономическими циклами Кондратьева. Более подробный анализ эволюции общества с точки зрения развития режима с обострением проводится в наших работах[440].

В частности, в статье «Глобальная динамика мирового сообщества» (2009) исследована последняя завершающая стадия развития в режиме с обострением, предшествующая демографическому переходу, выявлены процессы, непосредственно влияющие на демографический переход и обрисованы контуры будущей цивилизации.

Прослеживать существование и свойства эволюционных циклов Мир-Системы можно не только по анализу численности населения, но и по другому основному параметру порядка – по уровню развития технологий. Существованию и механизмам формирования экономических циклов посвящено множество исследований. Докапиталистическая эпоха, начиная с неолита, представляла собой культуру, основанную на экстенсивном земледелии. Тогда численность населения строго регулировалась потолком несущей способности Земли при данном уровне развития технологий, и возникали циклы, вызванные периодическими кризисами из-за относительной перенаселенности. Впервые такие циклы были описаны Т. Мальтусом в конце XVIII века, а их существование подтвердили В. Абель, Ф. Бродель и др. Идеи Мальтуса получили широкое распространение; известно, что их использовал Ч. Дарвин при создании теории биологической эволюции, в основе которой лежит борьба за существование и естественный отбор как аналог экономической конкуренции. Впоследствии весь объем производства стали называть потолком несущей способности Земли при имеющихся технологиях, а замедление и остановка роста населения из-за того, что рост производства продуктов питания отстает от прироста численности населения – мальтузианской ловушкой. В доиндустриальных обществах в мальтузианскую ловушку население попадало периодически, и в долгосрочной перспективе оставалось почти на уровне голодного выживания. Улучшение условий жизни по тем или иным причинам, например, как следствие победы в войне или перехода на новые технологии, или сокращение населения в результате эпидемии, всегда было временным и сопровождалось последующим бурным приростом населения, пока оно вновь не попадало в мальтузианскую ловушку.

В эпоху классического капитализма кризисы перенаселенности и связанные с ними циклы исчезли. Но возникли другие циклы, определяемые периодическими кризисами перепроизводства, величиной инвестиций, инфляции и др. Причины возникновения этих кризисов начали изучать Д. Юм, Д. Рикардо, К. Маркс и др. В прошлом столетии были открыты экономические циклы Китчина (2–4 года), Жюгляра (7-11 лет), Кузнеца (16–25 лет), Н. Д. Кондратьева (40–60 лет).

Наиболее изучены механизмы глобальных экономических циклов Кондратьева. Используя их, ученые сегодня научились делать прогнозы[441]. Выдающийся австро-американский ученый Н. Шумпетер одним из первых разработал теорию экономических циклов. Он утверждал, что все циклы генерируются инновациями. Экономические инновации рождаются и начинают формироваться в период кризиса, на стадии депрессии.

По аналогии демографическими циклами, описанными выше на языке пространственно-временных структур, этапы развития экономического цикла можно анализировать как динамику структуры, отражающую плотность распределения обобщенного уровня развития технологий Р по виртуальному рыночному пространству. В период депрессии инновационный процесс запускается благодаря потоку инвестиций в истощенную экономическую систему[442]. Вслед за отдельными инноваторами, внедряющими в производство новые товары, передовые технологии, осваивающими новые рынки сбыта, в новые сферы массово устремляются другие предприниматели, благодаря которым инновации охватывают все большее число взаимозависимых отраслей. Этот период соответствует этапу «растекания» структуры от центральных мест на периферию. Постепенно в экономике возникает оживление, подъем, массовый спрос на средства производства, сырье и рабочую силу. Подъем экономики сопровождается сокращением безработицы, ростом заработной платы и доходов, повышением спроса на потребительские товары и ростом цен на них. Расширение структуры по пространству заканчивается, начинается ее активный рост. Постепенно рынок инноваций переживает период насыщения и начинает выравниваться; инновации становятся традиционной частью экономики. Цены на товары начинают падать, а издержки их производства расти. Происходит нарастающее сокращение инвестиций вследствие ослабления предпринимательской активности. Компании, находящиеся на сходном уровне развития, активно конкурируют между собой, постепенно вытесняя с рынка более отсталые. Часто происходит слияние, объединение компаний в более крупную компанию, способную выдерживать конкурентную борьбу. В результате такого «естественного отбора» на рынке остается небольшое число компаний-гигантов. Происходит все большая монополизация экономики, т. е. концентрация экономического развития в центре и выпадение из развития «периферии» – мелких и более слабых структур. Это этап взрывного роста структуры, сопровождающийся все большим расслоением по уровню развития и нарастающей неустойчивостью. Он заканчивается неизбежным глобальным экономическим кризисом. Кризис преодолевается только тогда, когда старая структура экономики начинает уступать место новым отраслям производства, новым формам организации и регулирования экономики, т. е. за счет инновационного процесса. По выходе из кризиса система приобретает не одну технологическую новинку, а целый пакет социально-экономических инноваций, новых типов связей структур и организаций. Таким образом, происходит усложнение всей экономической системы в целом, и начинается новый виток эволюции, новый цикл развития.

Заключение

Рассмотренные в этой главе принципы эволюции – развитие в режиме с обострением, наличие циклов вокруг основного тренда, общее усложнение системы в ходе развития, сжатие масштабов и по времени, и по пространству, нарастание неустойчивости, конкурентная борьба (или естественный отбор) структур, находящихся на сходном уровне сложности – присущи всем сложным системам. Эволюция человеческого сообщества послужила здесь примером, проиллюстрированным результатами математического моделирования.