Общие требования к рисункам

Постарайтесь последовать нескольким нашим советам:

1. Если можно изобразить процесс во времени, сделайте это (рис. 13).

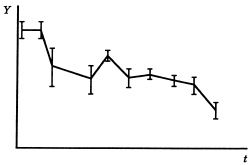
Рис. 13. Величина Y за время t статистически значимо снизилась

2. Вдоль осей координат должно быть от трех до пяти числовых обозначений (для остальных достаточно пустых меток на оси) – см. рис. 14.

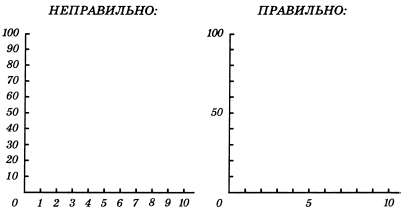
Рис. 14. Не надо рисовать слишком подробные шкалы—в них трудно ориентироваться. Все равно читатель смотрит только на 2–3 узловые точки каждой шкалы, а остальное—достраивает в своем воображении. Даже длинные слова мы не читаем полностью (только их начала и концы)

3. На одном рисунке должно быть от одной до трех кривых (рис. 15 и 16).

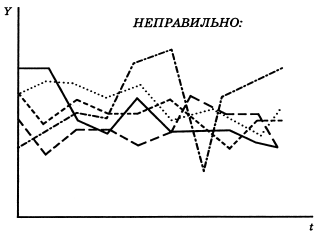
Рис. 15. Здесь слишком много кривых, для того чтобы быстро проследить каждую из них взглядом. Не надо требовать от читателя очень уж большого усердия, не надо перекладывать на него часть Вашей работы

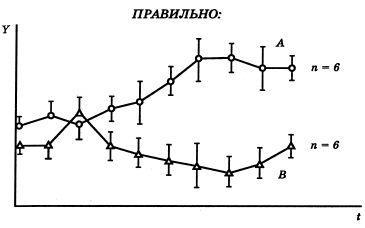
Рис. 16. Если на рисунке только две кривых, читатель легко оценит динамику обеих. Представлены средние ± ошибки средних; n– число объектов (больных, лабораторных животных, опытных образцов и т. п.); t – время. Звездочки соответствуют статистической значимости различий между Aи B: *р < 0,05; **р < 0,01. Никто не запрещает Вам вынести остальные кривые в другой рисунок или сделать серию рисунков, в каждом из которых новая кривая будет дана в сравнении с одной и той же повторяющейся кривой, например A и B, A и C, A и D и т. д.

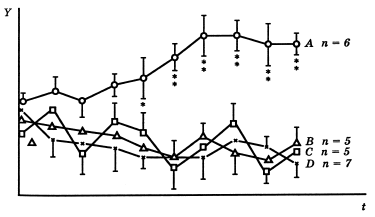
Рис. 17. Одна кривая настолько значительно отличается от остальных трех, что это позволяет свести большое количество кривых в один рисунок, не делая его при этом менее понятным. Представлены средние ± ошибки средних; n – число объектов; t – время. Звездочки соответствуют статистической значимости различий между A и B: *р < 0,05; **р < 0,01

Исключение из этого правила: только одна кривая существенно отличается от всех остальных (рис. 17).

4. Не забывайте обозначать статистический разброс значений средних. Несмотря на то что ни один солидный научный журнал не примет рисунков, на которых кривые даны без статистического разброса (средняя ± ошибка средней), диссертанты с удивительным упорством представляют в своих работах именно такие рисунки (рис. 18). Может быть, диссертанты не читают журналов или считают, что «сойдет и так»?

На рис. 18 ошибки средних не обозначены. Определенное суждение об изменении параметров A и B или о существовании различия между ними – невозможно.

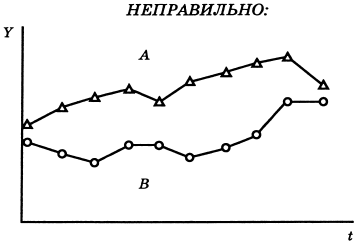
Рис. 18. Представлены только средние, статистический разброс не обозначен, данные о числе объектов в каждой выборке также отсутствуют. Суждение о различии между A и B – принципиально невозможно. t – время

При рассмотрении рис. 19 становится очевидным, что ни A, ни B не претерпевают значительных изменений и существенно не отличаются друг от друга. Согласно традиции, перекрывающиеся ошибки средних не изображаем.

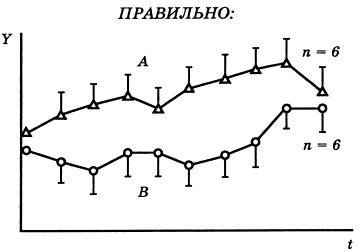
Рис. 19. Недостаток (см. рис. 18) исправлен: представлены средние ± ошибки средних и n – число объектов. В результате стало очевидным, что в данной серии опытов статистически значимого отличия A от B не установлено. t – время

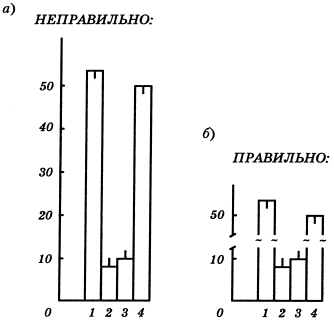
Рис. 20. Длинные столбики (а), если изображать их полностью, занимают слишком много места, ничего не добавляя к наглядности рисунка. Лучше вырезать их середину (б)

5) Не надо рисовать стрелки на концах осей абсцисс и ординат – это давно уже не принято.

6) Если Вы хотите в столбиковой диаграмме сравнить две или несколько величин, разница между которыми очень велика, или откажитесь от этой затеи, или не пытайтесь изобразить величины в истинном масштабе – используйте разрезы в столбиках (рис. 20).

Во всех случаях надо отдавать предпочтение методам, которые профессор А. Н. Максименков удачно назвал изобразительной статистикой.