Глава 32. Основные логические элементы

ЦЕЛИ

После изучения этой главы студент должен быть в состоянии:

• Перечислить и объяснить функции основных логических элементов.

• Нарисовать схематические обозначения для основных логических элементов.

• Начертить таблицы истинности для основных логических элементов.

Все цифровое оборудование, от простого до сложного, сконструировано с использованием небольшого количества основных схем. Эти схемы, называемые логическими элементами, выполняют некоторые логические функции с двоичными данными.

Существуют два основных типа логических схем: схемы принятия решений и память. Логические схемы принятия решений контролируют двоичные сигналы на входах и выдают выходной сигнал, основанный на состояниях входов и характеристиках логической схемы.

Схемы памяти используются для хранения двоичных данных.

32-1. ЭЛЕМЕНТ И

Элемент И — это логическая схема, имеющая два или более входа и один выход. На выходе элемента И появляется 1 только тогда, когда на все его входы поступает сигнал 1. Если на какой-либо из входов поступает 0, на выходе появляется 0.

На рис. 32-1 показаны стандартные обозначения, используемые для элементов И. Элемент И может иметь любое количество входов, большее одного.

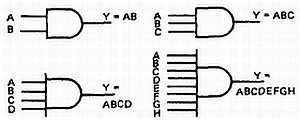
Рис. 32-1. Логические обозначения элемента И.

Показанные на рисунке обозначения представляют наиболее часто используемые элементы с двумя, тремя, четырьмя и восемью входами.

Работу элемента И отражает таблица на рис. 32-2. Такая таблица, называемая таблицей истинности, показывает выходное состояние элемента для любых возможных состояний входов.

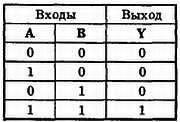
Рис. 32-2. Таблица истинности для двухвходового элемента И.

Входы обозначены А и В. Выход обозначен Y. Общее число возможных комбинаций в таблице истинности определяется следующей формулой:

N = 2ⁿ,

где N — общее количество возможных комбинаций, n — общее число входных переменных.

_{ПРИМЕР:}

_{Для двух входных переменных N = 2² = 4.}

_{Для трех входных переменных N = 2³ = 8.}

_{Для четырех входных переменных N = 2⁴ = 16.}

_{Для восьми входных переменных N = 2⁸ = 256.}

Элемент И выполняет операцию логического умножения. Логическое умножение известно как функция И.

Выход элемента И математически может быть представлен равенством Y = А ^ В или Y = АВ. Функция И — точка между двумя переменными А и В.

32-1. Вопросы

1. При каких условиях на выходе элемента И появляется 1?

2. Нарисуйте схематическое обозначение, используемое для элемента И с двумя входами.

3. Изобразите таблицу истинности для элемента И с тремя входами.

4. Какую логическую операцию выполняет элемент И?

5. Как алгебраически изображается операция, выполняемая элементом И?

32-2. ЭЛЕМЕНТ ИЛИ

На выходе элемента ИЛИ появляется 1, если на любой из его входов подана 1. На его выходе появляется 0, если на все его входы поданы 0. Значения на выходе элемента ИЛИ с двумя входами приведены в таблице истинности на рис. 32-3.

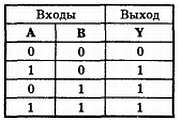
Рис. 32-3. Таблица истинности для двухвходового элемента ИЛИ.

Общее число возможных комбинаций выражается формулой N = 2² = 4. В таблице истинности приведены все четыре комбинации.

Элемент ИЛИ выполняет логическую операцию сложения. Алгебраически операция, выполняемая элементом ИЛИ, выражается следующим образом Y = А + В или Y = А V В. Знак плюс обозначает функцию ИЛИ.

На рис. 32-4 изображены логические обозначения для элемента ИЛИ. Входы обозначены А и В, а выход обозначен Y. Элемент ИЛИ может иметь любое число входов, большее одного. На рисунке изображены элементы ИЛИ с двумя, тремя, четырьмя и восемью входами.

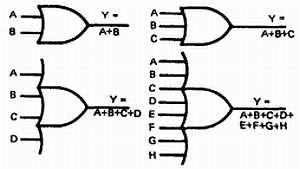
Рис. 32-4. Логические обозначения элемента ИЛИ.

32-2. Вопросы

1. При каких условиях на выходе элемента ИЛИ появляется 1?

2. Нарисуйте схематическое обозначение, используемое для элемента ИЛИ с двумя входами.

3. Изобразите таблицу истинности для элемента ИЛИ с тремя входами.

4. Какую логическую операцию выполняет элемент ИЛИ?

5. Как алгебраически изображается операция, выполняемая элементом ИЛИ?

32-3. ЭЛЕМЕНТ НЕ

Простейшей логической цепью является цепь НЕ. Она выполняет функцию, которая называется инверсией или отрицанием, и обычно называется инвертором. Цель инвертора — сделать состояние выхода противоположным состоянию входа. В логических цепях возможны два состояния — 1 и 0. Состояние 1 называют высоким, для указания, что напряжение в этом состоянии выше, чем в состоянии 0. Состояние 0 называют низким, для указания, что напряжение в этом состоянии ниже, чем в состоянии 1. Если 1, или высокое состояние, подано на вход инвертора, на выходе появится низкое состояние, или 0. Если на вход инвертора подать 0, или низкое состояние, то на выходе появится высокое состояние, или 1.

Работу инвертора отражает таблица на рис. 32-5.

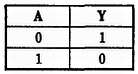
Рис. 32-5. Таблица истинности для инвертора.

Вход инвертора обозначен А, а выход А^- (читается «не А»). Черточка над буквой А показывает отрицание А. Поскольку инвертор имеет только один вход, то возможны только два состояния входа.

Схематическое обозначение инвертора или функции НЕ изображено на рис. 32-6. Треугольник обозначает схему, а кружочек обозначает инверсию или характеризует дополнение. Выбор схематического обозначения зависит от того, где инвертор используется. Если инвертор использует 1 в качестве указателя входа, применяется символ, изображенный на рис. 32-6(А). Если инвертор использует 0 в качестве указателя входа, берется символ, изображенный на рис. 32-6(Б).

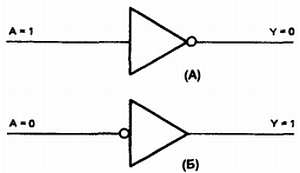
Рис. 32-6. Логические обозначения инвертора.

32-3. Вопросы

1. Какая операция выполняется цепью НЕ?

2. Изобразите таблицу истинности для цепи НЕ.

3. Нарисуйте схематические обозначения, используемые для цепи НЕ.

4. Почему для изображения цепи НЕ используются два различных символа?

32-4. ЭЛЕМЕНТ НЕ-И

Элемент НЕ-И является комбинацией инвертора и элемента И. Поэтому он и называется НЕ-И. Элемент НЕ-И является наиболее широко используемой логической функцией. Это обусловлено тем, что он может быть использован для создания элемента И, элемента ИЛИ, инвертора или любой комбинации этих функций.

Логическое обозначение элемента НЕ-И изображено на рис. 32-7. На рисунке также показана его эквивалентность последовательно включенным элементу И и инвертору. Кружочек на выходе обозначает инвертирование функции И.

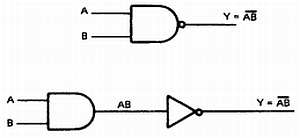
Рис. 32-7. Логические обозначения элемента И-НЕ.

На рис. 32-8 приведена таблица истинности для двухвходового элемента НЕ-И. Заметим, что выход элемента НЕ-И является дополнением выхода элемента И. Подача 0 на любой вход дает на выходе 1. Операция НЕ-И алгебраически выражается следующей формулой 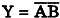, где Y — выход, а А и В — входы. Элементы НЕ-И существуют с двумя, тремя, четырьмя, восемью и тринадцатью входами.

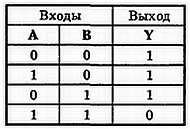
Рис. 32-8. Таблица истинности для двухвходового элемента И-НЕ.

Элементы НЕ-И наиболее доступны. Доступность и гибкость элементов НЕ-И позволяет использовать их в качестве элементов других типов. На рис. 32-9 показано, как элементы НЕ-И могут быть использованы для создания других логических функций.

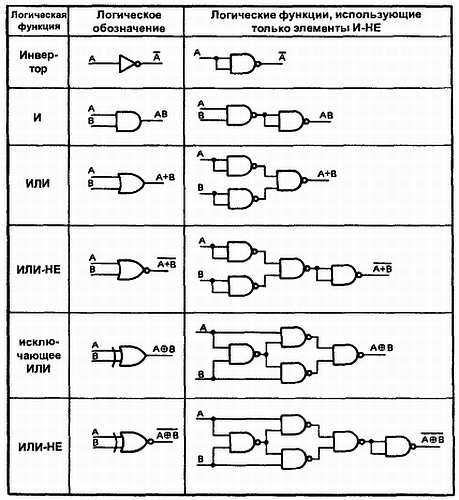
Рис. 32-9. Использование элемента И-НЕ для создания других логических функций.

32-4. Вопросы

1. Что такое элемент НЕ-И?

2. Почему элемент НЕ-И так часто используется в цепях?

3. Нарисуйте логический символ, используемый для обозначения элемента НЕ-И.

4. Как алгебраически изображается операция, выполняемая элементом НЕ-И?

5. Изобразите таблицу истинности для элемента НЕ-И с тремя входами.

32-5. ЭЛЕМЕНТ НЕ-ИЛИ

Элемент HE-ИЛИ является комбинацией инвертора и элемента ИЛИ. Поэтому он называется HE-ИЛИ. Подобно элементу НЕ-И, элемент HE-ИЛИ также может быть использован для создания элемента И, элемента ИЛИ или инвертора.

Логическое обозначение элемента НЕ-ИЛИ изображено на рис. 32–10. На рисунке также показана его эквивалентная схема, состоящая из последовательно включенных элемента ИЛИ и инвертора. Кружочек на выходе показывает инвертирование функции ИЛИ.

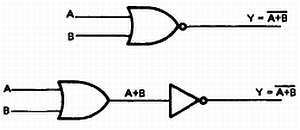
Рис. 32–10. Логические обозначения элемента ИЛИ-НЕ.

На рис. 32–11 изображена таблица истинности для двухвходового элемента HE-ИЛИ. Заметим, что его выход является дополнением выхода элемента ИЛИ. 1 на выходе появляется только тогда, когда на оба входа поданы 0. Если на все входы подана 1, то на выходе будет 0. Операция НЕ-ИЛИ алгебраически выражается следующей формулой 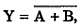, где Y — выход, а А и В — входы. Существуют элементы HE-ИЛИ с двумя, тремя, четырьмя и восемью входами.

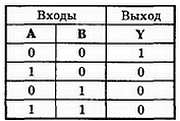
Рис. 32–11. Таблица истинности для двухвходового элемента ИЛИ-НЕ.

32-5. Вопросы

1. Что такое элемент НЕ-ИЛИ?

2. Почему элемент НЕ-ИЛИ полезен при проектировании цифровых цепей?

3. Нарисуйте символ, используемый для обозначения элемента НЕ-ИЛИ.

4. Как алгебраически изображается операция, выполняемая элементом НЕ-ИЛИ?

5. Изобразите таблицу истинности для элемента НЕ-ИЛИ с тремя входами.

32-6. ЭЛЕМЕНТЫ ИСКЛЮЧАЮЩЕЕ ИЛИ И ИСКЛЮЧАЮЩЕЕ НЕ-ИЛИ

Реже встречающимся, но все же важным элементом является элемент исключающее ИЛИ. Элемент исключающее ИЛИ имеет только два входа в отличие от элемента ИЛИ, который может иметь несколько входов. Однако элемент исключающее ИЛИ подобен элементу ИЛИ в том, что он выдает на выходе 1, когда на какой-либо из входов подана 1. Когда же на оба входа подаются 1 или 0, на выходе элемента исключающее ИЛИ будет 0. В то время как при подаче двух 1 на вход элемента ИЛИ на выходе будет 1.

Схематическое обозначение элемента исключающее ИЛИ изображено на рис. 32–12. На рис. 32–13 изображена таблица истинности для элемента исключающее ИЛИ.

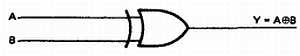
Рис. 32–12. Логическое обозначение элемента исключающее ИЛИ.

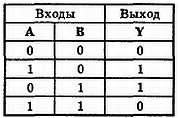
Рис. 32–13. Таблица истинности для элемента исключающее ИЛИ.

Операция исключающее ИЛИ алгебраически выражается следующей формулой Y = A 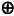 B. Здесь  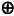— символ суммирования по модулю 2.

Дополнением к элементу исключающее ИЛИ является элемент исключающее ИЛИ-НЕ. Его схематическое обозначение показано на рис. 32–14. Кружочек на выходе означает инверсию или дополнение.

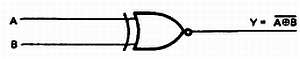
Рис. 32–14. Логическое обозначение элемента исключающее ИЛИ-НЕ.

На рис. 32–15 изображена таблица истинности для элемента исключающее ИЛИ-НЕ.

Операция исключающее ИЛИ-НЕ алгебраически выражается следующей формулой .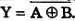

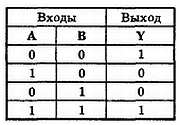
Рис. 32–15. Таблица истинности для элемента исключающее ИЛИ-НЕ.

32-6. Вопросы

1. В чем различие между элементом ИЛИ и элементом исключающее ИЛИ?

2. Нарисуйте символ, используемый для обозначения элемента исключающее ИЛИ.

3. Изобразите таблицу истинности для элемента исключающее ИЛИ.

4. Нарисуйте символ, используемый для обозначения элемента исключающее ИЛИ-НЕ.

5. Запишите алгебраические выражения для операций исключающее ИЛИ и исключающее ИЛИ-НЕ.

РЕЗЮМЕ

• На выходе элемента И появляется 1 тогда, когда на все его входы поступает сигнал 1.

• Элемент И выполняет операцию логического умножения.

• На выходе элемента ИЛИ появляется 1, если на любой из его входов подана 1.

• Элемент ИЛИ выполняет логическую операцию сложения.

• Элемент НЕ выполняет функцию, которая называется инверсией или отрицанием.

• Элемент НЕ преобразует входное состояние в противоположное выходное состояние.

• Элемент НЕ-И является комбинацией элемента И и инвертора.

• Подача 0 на любой вход элемента НЕ-И дает на выходе 1.

• Элемент НЕ-ИЛИ является комбинацией элемента ИЛИ и инвертора.

• 1 на выходе элемента НЕ-ИЛИ появляется только тогда, когда на оба входа поданы 0.

• 1 на выходе элемента исключающее ИЛИ появляется только тогда, когда уровни его входов различны.

• 1 на выходе элемента исключающее ИЛИ-НЕ появляется только тогда, когда уровни его входов одинаковы.

Глава 32. САМОПРОВЕРКА

1. Нарисуйте схематическое обозначение шестивходового элемента И.

2. Изобразите таблицу истинности для четырехвходового элемента И.

3. Нарисуйте схематическое обозначение шестивходового элемента ИЛИ.

4. Изобразите таблицу истинности для четырехвходового элемента ИЛИ.

5. Каково назначение элемента НЕ?

6. Чем отличается инвертор для входного сигнала от инвертора для выходного сигнала?

7. Нарисуйте схематическое обозначение для восьмивходового элемента НЕ-И.

8. Изобразите таблицу истинности для четырехвходового элемента НЕ-И.

9. Нарисуйте схематическое обозначение для восьмивходового элемента НЕ-ИЛИ.

10. Изобразите таблицу истинности для четырехвходового элемента НЕ-ИЛИ.

11. В чем особенность элемента исключающее ИЛИ?

12. Какое максимальное количество входов может иметь элемент исключающее ИЛИ-НЕ?