Измерение шума и источники шума

Определение эквивалентного напряжения шума, тока шума, а отсюда и коэффициента шума и отношения сигнал/шум для любого заданного источника — довольно примитивный процесс. Из него получаются все данные о шуме усилителя, которые могут вас интересовать. В основном этот процесс состоит в приложении ко входу известного шумового сигнала, а затем-в измерении амплитуды на выходе в определенной полосе частот. В некоторых случаях (например, при согласованном входном полном сопротивлении источника и устройства, как это бывает в усилителях радиочастоты) источник сигнала можно заменить генератором с точно известной и управляемой амплитудой колебаний.

Ниже мы обсудим методы и аппаратуру, которые понадобятся для измерения выходного напряжения и ограничения полосы измерения, а сейчас предположим, что вы можете измерять эффективное значение выходного сигнала при той полосе измерений, которую вы выберете.

7.18. Измерение без источника шума

В каскаде усилителя на биполярных или полевых транзисторах, предназначенного для работы на низких и средних частотах, желательно большое входное сопротивление. Мы хотим знать е_ш и i_ш, чтобы уметь предсказать отношение сигнал/шум для источника сигнала с произвольным уровнем и внутренним сопротивлением, как обсуждалось выше. Процедура эта проста. Во-первых, путем непосредственного измерения определяется коэффициент усиления по напряжению K_U для сигналов интересующего нас частотного диапазона. Амплитуда их должна быть достаточна, чтобы сделать незаметным собственный шум усилителя, но не настолько велика, чтобы привести усилитель в насыщение.

Во-вторых, закорачивается вход усилителя и измеряется среднеквадратичное напряжение шума на выходе е_{к. з}. Получаем напряжение входного шума на корень из герца по выражению

i_ш = е_{к. з}/(K_UB^1/2) В/Гц^1/2,

где В — ширина полосы измерения (см. разд. 7.21).

В-третьих, присоединив к входным клеммам резистор R, измеряем новое значение среднеквадратичного напряжения шума на выходе е_r. Значение сопротивления резистора должно быть достаточно большим, чтобы была заметна величина появившегося шума тока, но не настолько, чтобы доминировало входное сопротивление усилителя. (Если это практически невозможно, то оставьте вход разомкнутым и используйте в качестве R входное сопротивление усилителя.) Измеренное напряжение на выходе удовлетворяет соотношению

е²_r = [е²_ш + 4kTR + (i_шR)²]BK²_U,

откуда находится i_ш

i_ш = (1/R)[(е²_r/BK²_U) — (е²_ш + 4kTR)]^1/2

Если «немножко повезет», то иметь значение будет лишь первое слагаемое под корнем (т. е. шум тока преобладает над шумом напряжения усилителя и над тепловым шумом резистора, вместе взятыми). Теперь найдем отношение сигнал/шум для сигнала U_и с полным сопротивлением источника R_и

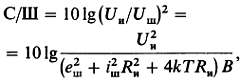
где числитель — квадрат напряжения сигнала (предполагается, что он лежит внутри полосы В), а слагаемые знаменателя — это квадраты напряжения шума усилителя, тока шума усилителя, проходящего через сопротивление R_и, и теплового шума R_и. Заметьте, что расширение полосы пропускания усилителя сверх пределов, необходимых для прохождения сигнала U_и, только уменьшает окончательное значение отношения сигнал/шум. Но если сигнал U_и широкополосный (например, он сам является шумом), то окончательное значение отношения сигнал/шум не зависит от ширины полосы усилителя. Во многих случаях в приведенном выражении преобладает одно из слагаемых.

7.19. Измерение с источником шума

Описанная техника измерения шумовых характеристик усилителя обладает тем преимуществом, что для нее не требуется точного и регулируемого источника шума, но зато нужен точный вольтметр и фильтр, а также должна быть известна частотная характеристика коэффициента усиления усилителя при данном сопротивлении подключенного источника. В альтернативном методе измерения шума предполагается подача на вход широкополосного шумового сигнала известной амплитуды и наблюдение за возрастанием напряжения выходного шума. Хотя эта методика требует точно калиброванного источника шума, зато не нужно никаких предположений о свойствах усилителя, так как характеристики шума измеряются прямо в интересующей нас точке — на входе.

Опять-таки необходимые измерения проводятся относительно просто. Генератор шума вы подсоединяете ко входу усилителя, будучи уверенными в том, что его полное сопротивление R_г — то самое, которое будет у источника, намеченного для работы с этим усилителем. Сначала вы определяете эффективное выходное напряжение шума усилителя при ослаблении источника шума до уровня нулевого выходного сигнала, затем увеличиваете среднеквадратичную амплитуду напряжения источника шума U_г до тех пор, пока выходной сигнал усилителя не увеличится на 3 дБ; это соответствует умножению среднеквадратичного напряжения на 1,414. Значение напряжения входного шума в полосе измерения при данном значении сопротивления источника равно значению добавленного сигнала. Таким образом усилитель имеет коэффициент шума

КШ = 10·lg(U²_г/4kTR_г).

Отсюда можно получить значение отношения сигнал/шум для сигнала любой амплитуды с тем же сопротивлением источника, пользуясь формулой, приведенной в разд. 7.12:

С/Ш = 10·lg(U²_и/4kTR_и) — КШ(R_и) дБ.

Существуют хорошие доступные калиброванные источники шума, большинство из которых предоставляют возможность ослабления до прецизионного уровня в микровольтовом диапазоне. Отметим еще раз: в приведенных формулах предполагается, что R_вх >> R_и. С другой стороны, если измерение коэффициента шума производится с согласованным источником сигнала, т. е. если R_и = Z_вх, то в предыдущих выражениях необходимо опустить коэффициент 4.

Заметим, что этим способом е_ш и i_ш прямо не определяются, находится только определенная комбинация для источника с сопротивлением, равным сопротивлению возбуждающего генератора, который используется при измерении. Конечно, после нескольких таких измерений с разными сопротивлениями источника вы можете в результате вывести значения е_ш и i_ш.

Превосходной вариацией этого метода является использование теплового шума резистора в качестве «источника шума». Это излюбленный прием разработчиков усилителей радиочастоты с очень малым уровнем шума (в которых обычно полное сопротивление источника сигнала равно 50 Ом, и оно согласовано с полным входным сопротивлением усилителя). Делается это обычно следующим образом. В сосуд Дьюара с жидким азотом помещается 50-омная «заглушка» (так на профессиональном жаргоне называется хорошо спроектированный резистор с пренебрежимо малой индуктивностью или емкостью), так что она имеет температуру кипящего азота 77 К; вторая заглушка 50 Ом находится при комнатной температуре. Вход усилителя попеременно подключается к этим двум резисторам (обычно с помощью высококачественного коаксиального реле), в то время как мощность шума на выходе (на некоторой центральной частоте при некоторой полосе измерения) измеряется с помощью измерителя мощности радиочастоты. Назовем результаты этих двух измерений мощности выходных шумов для холодного и теплого резисторов соответственно R_хол и R_тепл. Легко показать, что температура шума усилителя на частоте измерения равна

T_ш = (T_тепл - T_хол)/(Y — 1),

где Υ = R_тепл/R_хол есть отношение мощностей шума. Отсюда, воспользовавшись формулой из разд. 7.12, имеем для коэффициента шума

КШ(дБ) = 10·lg(Т_ш/290 + 1).

_{Упражнение 7.6. Выведите предыдущее выражение для температуры шума. Подсказка: для начала примите, что Rтепл = α(Тш + Tтепл) и Rхол = α(Тш + Tхол), где α — константа, которая скоро сократится; обратите внимание также на то, что вклад шума усилителя, обозначенный как температура шума, добавляется к температуре шума резистора источника. Вычтите ее отсюда.}

_{Упражнение 7.7. Температура шума (или коэффициент шума) усилителя зависит от величины полного сопротивления источника сигнала Rи. Покажите, что усилитель, характеризующийся величинами еш и iш (как на рис. 7.46), имеет минимум температуры шума при полном сопротивлении источника Rи = еш/iш. Покажите, далее, что при этом значении Rи температура шума определяется формулой Тш = еш·iш/2k.}

Усилители с согласованным входным сопротивлением. Последний способ идеален для измерения шума усилителей, спроектированных в расчете на согласованное сопротивление источника сигнала. Наиболее частыми примерами таких усилителей являются радиочастотные усилители или приемники для работы с полным сопротивлением источника сигнала около 50 Ом и сами имеющие входное сопротивление 50 Ом. В гл. 13 мы обсудим причины отступления от нашего обычного критерия, который гласит, что источник сигнала должен иметь малое внутреннее полное сопротивление по сравнению с полным сопротивлением нагрузки, на которую он работает. В этом случае е_ш и i_ш по отдельности не важны, имеет значение только общий (с согласованным источником) коэффициент шума или некоторое специфицированное значение отношения сигнал/шум с согласованным источником сигнала оговоренной амплитуды.

Иногда шумовые параметры выражаются явно в виде амплитуды узкополосного сигнала, необходимого для получения определенного отношения сигнал/шум на выходе. Обычный радиоприемник может иметь специфицированное отношение сигнал/шум 10 дБ при среднеквадратичном напряжении входного сигнала 0,25 мкВ и ширине полосы 2 кГц. В этом случае процедура состоит в измерении среднеквадратичного напряжения выходного сигнала приемника в условиях возбуждения входа согласованным (по сопротивлению) источником синусоидального сигнала, вначале выведенным на ноль, а потом дающим возрастающий (синусоидальный) сигнал до тех пор, пока среднеквадратичный выходной сигнал не достигнет уровня 10 дБ; в обоих случаях ширина полосы приемника 2 кГц. Важно, чтобы используемый измерительный прибор давал истинное среднеквадратичное напряжение, когда шум и сигнал смешаны (подробнее об этом см. далее). Заметим, что при измерении радиочастотных шумов часто требуется работа с выходными сигналами звукового диапазона.

7.20. Генераторы шумов и сигналов

Широкополосный шум может генерироваться с помощью указанных ранее эффектов, а именно за счет теплового и дробового шума. Дробовой шум вакуумного диода является классическим источником широкополосного шума, который особенно удобен в работе, поскольку напряжение шума можно точно предсказать. С недавних пор в качестве источника шума все чаще применяется стабилитрон. Шумы обоих этих источников имеют спектр частот от нуля до очень больших значений, поэтому они полезны и при измерениях в звуковом диапазоне, и в радиодиапазоне.

Интересный источник шума можно построить с помощью цифровой аппаратуры, в частности длинных сдвиговых регистров, в которых на вход подается результат сложения по модулю 2 нескольких фиксированных разрядов (разд. 9.33). В результате образуется выходной сигнал в виде псевдослучайной последовательности нулей и единиц, которая после цифро-аналогового преобразования и прохождения через фильтр нижних частот порождает аналоговый сигнал в виде белого шума со спектром, простирающимся до точки среза фильтра; эта точка должна быть намного ниже частоты, с которой сдвигается регистр. Такие генераторы могут работать на очень высоких частотах, генерируя шум до 100 и более килогерц.

Этот «шум» обладает интересным свойством: по прошествии некоторого времени, определяемого длиной регистра, он в точности повторяется (регистр максимальной длины n бит перед повторением проходит через 2ⁿ — 1 состояний). Этот период без особого труда можно продлить на месяцы или годы, хотя секунд, как правило, достаточно. Например, 50-разрядный регистр, сдвигаемый с частотой 10 МГц, генерирует белый шум со спектром до 100 кГц и временем повторения 3,6 года. Аппаратура для генерации псевдослучайного шума на базе этого метода описана в разд. 9.36.

Некоторые источники шума могут генерировать и белый, и розовый шум. У розового шума равные мощности на каждой октаве, а не на каждой частоте. Плотность его мощности (мощность на герц) имеет спад 3 дБ/октава, и, поскольку RС-фильтр имеет спад 6 дБ/октава, для генерации розового шума из белого необходим довольно сложный фильтр. Схема, представленная на рис. 7.61, работает от ИМС 23-разрядного цифрового генератора белого шума и дает на выходе розовый шум с точностью ±0,25 дБ от 10 Гц до 40 кГц.

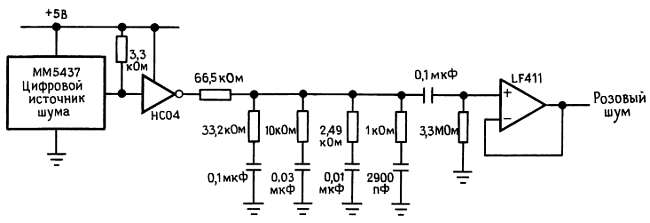
Рис. 7.61. Источник розового шума (— 3 дБ/октава, ±0,25 дБ от 10 Гц до 40 кГц).

Выпускаются самые разнообразные источники сигнала с прецизионно-регулируемой амплитудой выходного сигнала (вплоть до микровольтового диапазона и ниже) и частотой от долей герца до гигагерц. Некоторые из них могут программироваться по цифровой «шине». В качестве примера — синтезирующий генератор сигнала, модель 8660 Hewlett-Packard, с частотой выходного сигнала от 0,01 до 110 МГц и амплитудой выходного сигнала, калиброванной от 10 нВ до 1В (среднеквадратичное напряжение), с удобным цифровым дисплеем, шиной внешних соединений (интерфейсом) и шикарными приставками для расширения полосы частот до 2,6 ГГц для модуляции и качания частоты. Это несколько больше, чем обычно нужно для работы.

7.21. Ограничение полосы частот и измерение среднеквадратичного (эффективного) напряжения

Ограничение полосы частот. Во всех измерениях, о которых говорилось, предполагается, что шум на выходе рассматривается в ограниченной полосе частот. В некоторых случаях усилитель может иметь приспособления для такого ограничения, что облегчает работу. Если это не так, то приходится присоединять к выходу усилителя какой-нибудь фильтр, и уже потом измерять напряжение шума на выходе фильтра.

Проще всего использовать обычный RС-фильтр с точкой, отвечающей значению — 3 дБ, установленной примерно на край нужной полосы. Для точного измерения шума необходимо знать эквивалентную «полосу шума», т. е. ширину полосы совершенного «прямоугольного» фильтра нижних частот, через который бы проходило такое же напряжение шума (рис. 7.62).

B = (π/2)f_{_3 дБ} = 1,57/f_{_3 дБ}.

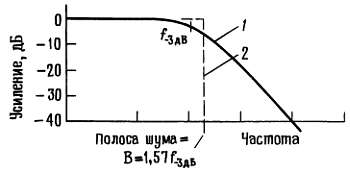
Рис. 7.62. Эквивалентная «прямоугольному фильтру» полоса шума RС-фильтра нижних частот. 1 — RC-фильтр (20 дБ/декада); 2 — эквивалентная идеальная характеристика.

Значение ширины этой полосы подставляется вместо В в приведенных выше выражениях. После несложных выкладок находим: Для пары каскадно соединенных RC-фильтров (развязанных таким образом, чтобы они не нагружали друг друга) магическим выражением будет В = 1,22/f_{_3 дБ}. Для фильтра Баттерворта, описанного в разд. 5.05, ширина полосы шумов такова:

В = 1,57·f_{_3 дБ} … 1 полюс

В = 1,11·f_{_3 дБ} … 2 полюса

В = 1,05·f_{_3 дБ} … 3 полюса

В = 1,025·f_{_3 дБ} … 4 полюса

Если вы хотите провести измерения в ограниченной полосе частот около некоторой средней частоты, то можете использовать просто пару RС-фильтров (рис. 7.63); в этом случае полоса частот будет иметь указанный вид.

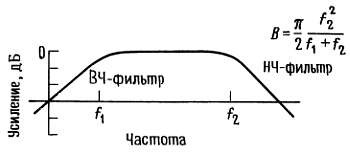
Рис. 7.63. Эквивалентная «прямоугольному фильтру» полоса шума полосового RС-фильтра.

Если у вас уже есть опыт контурного интегрирования, можете попробовать сделать следующее упражнение:

_{Упражнение 7.8. (Факультативное.) Выведите предыдущий результат прямо из свойств характеристик RС-фильтров. Предположите, что мощность входного сигнала равна единице на герц и проинтегрируйте выходную мощность от нуля до бесконечности. Контурный интеграл и будет искомым ответом.}

Другой способ изготовить полосовой фильтр для измерения шума — это использовать RLC-схему. Это лучше, чем пара каскадно соединенных RС-фильтров верхних и нижних частот, если вы хотите провести измерения в полосе, узкой в сравнении с центральной частотой (т. е. с высоким Q). На рис. 7.64 показаны как параллельная, так и последовательная RLС-схема, а также точные формулы, определяющие их полосы пропускания; для обеих схем резонансная частота f₀ = 1/2π√(LC)

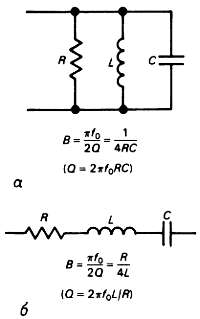
Рис. 7.64. Эквивалентная «прямоугольному фильтру» полоса шума полосового RLC-фильтра.

Вы можете сформировать схему полосового фильтра в виде параллельной коллектору (или стоку) RLС-нагрузки; в этом случае используются приведенные выражения. Другой вариант: можно ввести фильтр, как показано на рис. 7.65; с точки зрения пропускания шумов в определенной полосе эта схема в точности эквивалентна параллельной RLC-цепи при R = R₁||R₂.

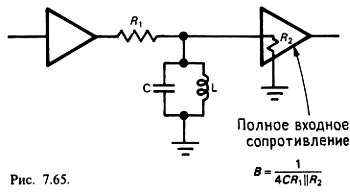
Измерение напряжения шума. Наиболее точный способ измерения выходного шума — использование выверенного вольтметра среднеквадратичного (эффективного) напряжения. Он работает путем измерения нагрева, производимого соответственно усиленным сигналом, или с использованием аналоговой схемы возведения в квадрат с последующим усреднением. Если вы пользуетесь измерителем истинного среднеквадратичного значения, то сначала проверьте, рассчитан ли он на те частоты, на которых проводятся измерения, потому что некоторые такие приборы имеют частоту всего несколько килогерц. Измерители истинного среднеквадратичного напряжения специфицируются также по пик-фактору, т. е. предельному отношению пикового напряжения к среднеквадратичному, при котором нет больших потерь точности. При измерении нормальных (гауссовских) шумов достаточно иметь пик-фактор от трех до пяти.

При отсутствии среднеквадратичного вольтметра можно воспользоваться простым осредняющим вольтметром переменного тока. Но в этом случае показания прибора приходится корректировать. Дело в том, что все осредняющие вольтметры (VOM, DMM и т. п.) изначально настроены так, что показывают не среднее напряжение, а среднеквадратичное напряжение в предположении синусоидальности сигнала. Например, если измерить напряжение электросети в США, то вольтметр покажет приблизительно 117 В. Это прекрасно, но, так как вы измеряете гауссовский шум, то придется применить дополнительную коррекцию. Правило здесь такое: чтобы получить среднеквадратичное напряжение гауссовского шума, следует показания осредняющего вольтметра переменного тока умножить на 1,13 или добавить 1 дБ.

Предупреждение: это правило хорошо работает, если измеряется чистый шум (т. е. выходной сигнал усилителя с резистором или генератором шума на входе), но оно не дает точного значения, если к шуму добавлен синусоидальный сигнал.

Третий метод (не очень точный) состоит в наблюдении шумовой картины на экране осциллографа: среднеквадратичное напряжение равно от 1/6 до 1/8 значения разности пиков (разброс зависит от вашей субъективной оценки этой величины). В этом методе хотя и неточном, не возникает проблем с получением достаточной полосы измерения.

7.22. Попурри на тему шумов

Вот подборка интересных и, возможно, полезных фактов.

1. Время осреднения, необходимое для того, чтобы в показывающем приборе флуктуации выпрямленного шумового сигнала уменьшились до требуемого уровня при заданной полосе шумов, равно

τ ~= 1600/Bσ² с,

где τ — постоянная времени показывающего прибора, необходимая для того, чтобы создать на выходе линейного детектора, возбуждаемого на входе шумом с полосой В, флуктуации со стандартным отклонением σ процентов.

2. Для белого шума с ограниченной полосой ожидаемое количество максимумов в секунду равно

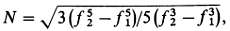
где f₁ и f₂ - нижняя и верхняя границы полосы. Для f₁ = 0 N = 0,77f₂ ; для узкополосного шума (f₁ ~= f₂) N ~= (f₁ + f₂)/2.

3. Отношение среднеквадратичного значения к среднему составляет: для гауссовского шума эфф/ср = √(π/2) = 1,25= 1,96 дБ,

для синусоидального сигнала эфф/ср = π/2^3/2 = 1,11 =0,91 дБ, для прямоугольного сигнала эфф/ср = 1 = 0 дБ.

4. Частоты появления амплитуд в гауссовском шуме. Рис. 7.66 показывает долю времени, когда данный уровень амплитуды превышается гауссовским шумом (мгновенным значением), имеющим эффективное значение 1 В.

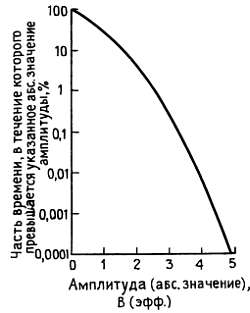
Рис. 7.66. Относительная наблюдаемость амплитуд в гауссовском шуме.