Псевдослучайные двоичные последовательности и генераторы шума

9.32. Цифровые методы генерации шума

Псевдослучайные двоичные последовательности являют собой пример гармоничного сочетания аналоговой и цифровой техники. Оказывается, можно необычайно просто генерировать последовательности бит (или слов), с хорошими стохастическими свойствами, т. е. последовательности, которые будут обладать такими же вероятностными и корреляционными свойствами, какими обладает идеальная машина для подбрасывания монеты. Поскольку эти последовательности генерируются стандартными элементами детерминированной логики (если быть точнее, регистрами сдвига), получающиеся двоичные последовательности на самом деле являются предсказуемыми и повторяемыми, хотя любой фрагмент такой последовательности во всех отношениях выглядит как случайная последовательность 0 и 1. Всего с помощью нескольких ИМС можно получить последовательности, которые тянутся буквально на столетия без повторения; это очень простой и привлекательный способ получения цифровых двоичных последовательностей или аналоговых сигналов шума.

Действительно, существует даже недорогая ИМС «цифровой источник шума», выпускаемая в корпусе мини-DIP (ММ5437 фирмы National), а генераторы шума на регистрах сдвига входят в состав технических средств многих ИМС, создающих звуковые эффекты.

Аналоговый шум. С помощью простой фильтрации нижних частот псевдослучайной двоичной последовательности (ПСП) можно получить гауссов белый шум с ограниченной полосой, т. е. напряжение шума с плоским энергетическим спектром до некоторой частоты среза (более подробно о шумах см. гл. 7). С другой стороны, с помощью взвешенного суммирования содержимого регистров сдвига (с использованием набора резисторов) можно осуществить цифровую фильтрацию. С помощью этого способа можно легко получить плоский спектр шума в пределах нескольких мегагерц. Позже вы увидите, что источники аналогового шума, синтезированные цифровым способом, имеют целый ряд преимуществ перед чисто аналоговыми способами, использующими шумящие диоды или резисторы.

Другие области применения. Кроме таких очевидных применений, как аналоговые или цифровые источники шума, ПСП полезны в целом ряде других областей, ничего общего не имеющих с шумами. Их можно использовать для шифрования сообщений или данных, поскольку идентичный генератор ПСП на приемном конце дает ключ к шифру. ПСП широко используются в кодах, обнаруживающих и исправляющих ошибки, так как они позволяют видоизменить блоки данных таким образом, что правильные кодовые сообщения будут находится друг от друга на максимально возможном «расстоянии Хэмминга» (измеряется числом позиций с разными данными). Обладая хорошими автокорреляционными свойствами, они являются идеальными как коды для радиолокационных систем, в которых ответный сигнал сравнивается (точнее взаимно коррелируется) с передаваемой битовой последовательностью. Их можно использовать даже как компактные делители по модулю n.

9.33. Последовательности, генерируемые регистрами сдвига с обратными связями

Наиболее известным (и самым простым) генератором ПСП является регистр сдвига с обратной связью (рис. 9.82).

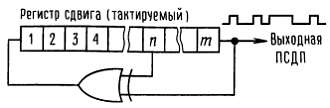
Рис. 9.82. Генератор псевдослучайной двоичной последовательности.

Регистр сдвига длины m работает от тактовых импульсов с частотой f₀. Входная последовательность формируется с помощью вентиля ИСКЛЮЧАЮЩЕЕ ИЛИ, на вход которого поступают сигналы от n-го и последнего (m-го) разрядов регистра сдвига. Такая схема проходит через некоторое множество состояний (совокупность состояний регистра сдвига после каждого тактового импульса), которые после К тактов начинают повторяться, т. е. последовательность состояний является циклической с периодом К.

Максимальное число возможных состояний m-разрядного регистра равно К = 2^m, т. е. числу m-битовых двоичных комбинаций. Однако состояние «все нули» является «тупиком» для этой схемы, поскольку на выходе вентиля ИСКЛЮЧАЮЩЕЕ ИЛИ появляется 0, который вновь поступает на вход схемы. Таким образом, последовательность максимальной длины, которую может сформировать данная схема, содержит 2^m — 1 бит. Оказывается, что такую последовательность максимальной длины можно получить только при правильном выборе m и n, причем полученная последовательность будет псевдослучайной. (Критерием максимальной длины является неприводимость и примитивность многочлена 1 + хⁿ + х^m над полем Галуа). В качестве примера рассмотрим 4-разрядный регистр сдвига с обратной связью, показанный на рис. 9.83.

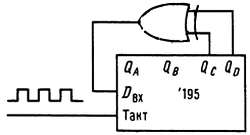
Рис. 9.83.

Начиная с состояния 1111 (можно было бы начать с любого другого состояния, за исключением 0000), можно записать состояния в порядке их следования:

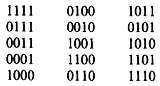
Мы записали эти состояния как 4-разрядные числа Q_AQ_BQ_CQ_D. Здесь 15 = (2⁴ - 1) различных состоянии, затем они повторяются вновь. Значит, это регистр максимальной длины.

_{Упражнение 9.6. Покажите, что 4-разрядный регистр с обратной связью от второго и четвертого разрядов не является регистром максимальной длины. Сколько существует различных последовательностей? Сколько состояний в каждой последовательности?}

Отводы обратной связи. Сдвиговые регистры максимальной длины можно выполнить с числом отводов в цепи обратной связи больше 2 (в этом случае используются несколько вентилей ИСКЛЮЧАЮЩЕЕ ИЛИ, соединенных в виде стандартного дерева четности, т. е. в виде суммы по модулю 2 нескольких разрядов). На самом деле, для некоторых значений m регистр максимальной длины можно сделать только в том случае, когда число отводов будет больше 2. Ниже перечислены все значения m до 40, для которых регистр максимальной длины реализуется с использованием ровно двух отводов, т. е. с обратной связью от n-го и m-го (последнего) разрядов по типу регистра, приведенного ранее.

Представлены также значения n и длина цикла К по числу тактов. В некоторых случаях подойдут и другие значения n и во всех случаях n можно заменить на m — n; таким образом, для предыдущего примера можно использовать отводы n = 1 и m = 4.

Длина регистров сдвига обычно кратна 8 и, возможно, как раз такую длину вы захотите использовать. В этих случаях может потребоваться более двух отводов. Вот эти магические числа:

В ИМС ММ5437 (генератор шума) используется 23-разрядный регистр с отводом от 18-го разряда. Внутренний тактовый генератор обеспечивает работу на частоте около 160 кГц; схема генерирует белый шум в диапазоне до 70 кГц (затухание 3 дБ) с временем цикла около 1 мин. На рис. 7.61 эта ИМС была использована в схеме генератора «розового шума». При использовании 33-разрядного регистра, работающего на частоте 1 МГц, время цикла будет около 2 ч. Время цикла 100-разрядного регистра, работающего на частоте 10 МГц, будет в миллион раз больше, чем возраст Вселенной!

Свойства последовательностей максимальной длины. Псевдослучайную последовательность двоичных символов мы получаем путем тактирования одного из таких регистров и наблюдения последовательных выходных двоичных символов. Выход можно взять от любого разряда регистра; обычно в качестве выхода используют последний (m-й) разряд. Последовательность максимальной длины обладает следующими свойствами:

1. В полном цикле (К тактов) число «1» на единицу больше, чем число «0». Добавочная «1» появляется за счет исключения состояния «все нули». Это свидетельствует о том, что «орлы» и «решки» равновероятны (дополнительная «1» большой роли не играет; 17-разрядный регистр будет вырабатывать 65 536 «1» и 65 535 «0» за один цикл).

2. В одном цикле (К тактов) половина серий из последовательных «1» имеет длину 1, одна четвертая серий — длину 2, одна восьмая — длину 3 и т. д. Такими же свойствами обладают и серии из «0» с учетом пропущенного «0». Это говорит о том, что вероятности «орлов» и «решек» не зависят от исходов предыдущих «подбрасываний» и поэтому вероятность того, что серия из последовательных «1» или «0» закончится при следующем подбрасывании равна 1/2 (вопреки обывательскому пониманию «закона о среднем).

3. Если последовательность полного цикла (К тактов) сравнить с этой же последовательностью, но циклически сдвинутой на любое число символов n (n не является нулем или кратным К), то число несовпадений будет на единицу больше, чем число совпадений. Научно выражаясь, автокорреляционная функция этой последовательности представляет собой дельта-функцию Кронекера при нулевой задержке и равна — 1/К при любой другой задержке. Отсутствие «боковых лепестков» автокорреляционной функции — это как раз то свойство, которое делает ПСП очень полезными в радиолокационных системах.

_{Упражнение 9.7. Покажите, что последовательность, полученная с помощью 4-разрядного регистра сдвига (с отводами n = 2, m = 4), удовлетворяет этим свойствам. В качестве «выхода» возьмите QΑ: 100010011010111.}

9.34. Формирование аналогового шума с использованием последовательностей максимальной длины

Преимущества шума, полученного цифровым способом. Как ранее уже отмечалось, цифровой выход регистра сдвига с обратной связью, вырабатывающего последовательность максимальной длины, можно преобразовать в белый шум с ограниченной полосой, используя фильтр нижних частот, частота среза которого существенно ниже тактовой частоты регистра. Прежде чем вдаваться в детали, покажем некоторые преимущества аналогового шума, полученного цифровым способом. Помимо всего прочего, при таком подходе появляется возможность генерировать шум с заданными спектром и амплитудой с подстройкой полосы (путем подстройки тактовой частоты), используя надежные и простые в обращении цифровые схемы.

Здесь отсутствуют нестабильность генераторов на шумящих диодах, проблемы взаимовлияния и помех, которые не дают покоя чувствительным маломощным аналоговым схемам диодных или резисторных генераторов шума. Наконец, цифровые схемы генерируют повторяемый «шум»; если его отфильтровать с помощью взвешенного цифрового фильтра (более подробно об этом несколько позже), то можно получить повторяемые колебания шума, независящие от тактовой частоты.

9.35. Энергетический спектр последовательности, сформированной при помощи регистра сдвига

Спектр выходного сигнала, генерируемого регистром сдвига максимальной длины, составляют колебания шума от частоты повторения всей последовательности f_такт/K до тактовой частоты и выше. До частоты 12 % от тактовой спектр имеет плоскую часть с неравномерностью ±0,1 дБ, затем наблюдается быстрое падение до уровня —0,3 дБ на частоте 44 % /такт. Таким образом, фильтр нижних частот с частотой среза в верхней области 5-10 % от тактовой частоты будет преобразовывать выходной сигнал регистра сдвига в аналоговое напряжение шума с ограниченной полосой. Для этой цели достаточен даже простой RC-фильтр, хотя, если возникает необходимость в точной полосе шума, то желательно использовать активные фильтры с крутой характеристикой на частоте среза (см. гл. 5).

Для того чтобы эти утверждения звучали более убедительно, обратимся к выходному сигналу регистра сдвига и его спектру. Обычно желательно исключить постоянную составляющую в цифровом сигнале, формируя выходной сигнал, в котором «1» соответствует напряжение +а В, а «0» — а В (рис. 9.84).

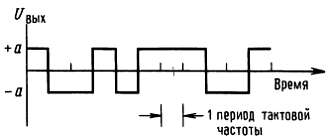
Рис. 9.84.

Это можно легко сделать с помощью двухтактного транзисторного каскада, показанного на рис. 9.85.

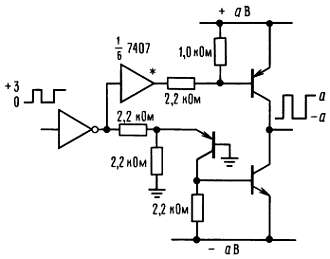
Рис. 9.85. Прецизионная биполярная выходная ступень с низким Z_вых.

Можно также использовать МОП-транзисторы, схемы стабилизации напряжения с фиксирующими диодами, быстродействующий операционный усилитель с регулировкой тока постоянной составляющей в точке суммирования или КМОП-ключ `4053, работающий от ±а В, с двумя входами, подключенными к источникам питания.

Как мы отмечали выше, автокорреляционная функция последовательности символов на выходе содержит один пик. Если состояния на выходе представить числами +1 и —1, то цифровая автокорреляционная функция будет иметь вид, показанный на рис. 9.86; (цифровая автокорреляция — это сумма произведений соответствующих разрядов при сравнении последовательности двоичных символов с ее сдвинутой копией). Не путайте ее с непрерывной автокорреляционной функцией, которую рассмотрим несколько позже.

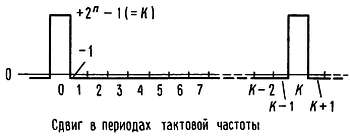
Рис. 9.86. Дискретная автокорреляционная функция для полного цикла максимальной последовательности.

Функция на этом графике определена только для сдвигов, соответствующих целому числу тактов. Для всех ненулевых сдвигов и сдвигов, не кратных общему периоду К, автокорреляционная функция постоянна и имеет значение — 1 (поскольку в последовательности есть дополнительная 1); по сравнению со значением функции при нулевом сдвиге (К) величина —1 пренебрежимо мала.

Если же неотфильтрованный выход регистра сдвига рассматривать как аналоговый сигнал (принимающий только два значения +а и — а), то нормализованная автокорреляционная функция будет, как показано на рис. 9.87, непрерывной. Другими словами, при сдвигах более чем на один такт вправо и влево корреляция между значениями сигнала полностью отсутствует.

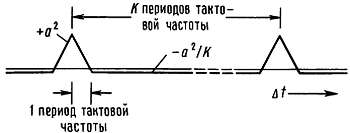
Рис. 9.87. Непрерывная автокорреляционная функция для полного цикла максимальной последовательности.

Энергетический спектр неотфильтрованного сигнала на выходе регистра сдвига можно получить по автокорреляционной функции, используя стандартные математические средства. В результате получаются равноудаленные серии пичков (дельта-функций), начинающихся с частоты повторения всей последовательности f_такт/K и затем идущих через равные интервалы f_такт/K. То, что спектр состоит из совокупности дискретных спектральных линий, отражает тот факт, что последовательность время от времени (периодически) повторяется. Пусть вас не удивляет странный вид спектра; он будет выглядеть непрерывным при любых изменениях и приложениях, которые занимают время, меньшее чем время цикла регистра. Огибающая спектра неотфильтрованного сигнала на выходе регистра показана на рис. 9.88. Она пропорциональна квадрату функции (sin х)/х. Обратите внимание на одно необычное свойство-на тактовой частоте и ее гармониках энергия шума равна нулю.

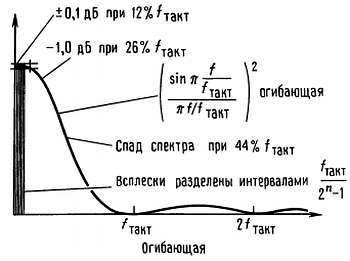
Рис. 9.88. Энергетический спектр неотфильтрованного сигнала на выходе регистра сдвига.

Напряжение шума. При генерации аналогового шума используется, разумеется, только часть низкочастотной области спектра. Оказывается, что удельную мощность шума на герц несложно выразить через половинную амплитуду а и тактовую частоту f_такт. Мощность, выраженная через среднеквадратичное напряжение шума, будет

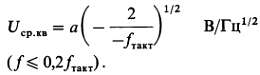
Это относится к нижней части спектра, т. е. к той части, которая обычно используется (для того чтобы определить плотность мощности в любой части спектра, можно использовать огибающую).

Предположим, например, что регистр сдвига максимальной длины работает на частоте 1,0 МГц и организован таким образом, что выходное напряжение изменяется от +10,0 до —10,0 В. Выходной сигнал пропускается через RC-фильтр нижних частот с затуханием 3 дБ на частоте 1 кГц (рис. 9.89).

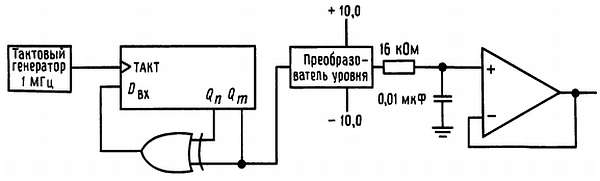
Рис. 9.89. Простой источник псевдослучайного шума.

Можно точно вычислить среднеквадратичное напряжение шума на выходе. Из предыдущего выражения мы знаем, что среднеквадратичное напряжение на выходе преобразователя уровней равно 14,14 мВ/Гц^1/2. Из разд. 7.21 мы знаем также, что полоса шума НЧ-фильтра составляет (π/2) (1,0 кГц) или 1,57 кГц. Поэтому выходное напряжение шума будет равно U_cp.кв = 0,01414·(1570)^1/2 = 560 мВ, а его спектр будет соответствовать низкочастотному RС-фильтру.

9.36. Низкочастотная фильтрация

Аналоговая фильтрация. Полезный спектр шума, создаваемого генератором псевдослучайной последовательности, простирается от низкочастотной границы, обратной периоду повторения (f_такт/K), до высокочастотной границы, равной примерно 20 % от тактовой частоты (на этой частоте мощность шума на герц падает на 0,6 дБ).

Простая низкочастотная фильтрация с использованием RС-звеньев, как показано в предыдущем примере, равнозначна установке точки 3 дБ намного ниже тактовой частоты (например, ниже 1 % f_такт). Для того чтобы использовать часть спектра более близкую к тактовой частоте, желательно применить фильтры с более крутым срезом, например фильтры Баттерворта или Чебышева. В этом случае плоскость результирующего спектра будет определяться параметрами фильтра, которые должны быть измерены, поскольку отклонения в параметрах могут вызывать колебания коэффициента передачи в полосе пропускания. С другой стороны, если требуется точное значение напряжения шума на Гц^-1/2, то необходимо измерить реальный коэффициент передачи фильтра по напряжению.

Цифровая фильтрация. Недостаток аналоговой фильтрации заключается в том, что если тактовая частота изменяется в несколько раз, то требуется подстройка частоты среза фильтра. В тех случаях, где это необходимо, изящное решение дает цифровая фильтрация, которая осуществляется с помощью взвешенной аналоговой суммы последовательных выходных разрядов (нерекурсивная цифровая фильтрация). С ее помощью эффективная частота среза подстраивается под изменение тактовой частоты. Кроме того, цифровая фильтрация позволяет спуститься до предельно низких частот среза (доли герца), где аналоговая фильтрация становится практически беспомощной.

Для того чтобы осуществить взвешенное суммирование одновременно нескольких последовательных выходных разрядов, можно просто воспользоваться различными параллельными выходами разрядов регистра сдвига и использовать резисторы различного номинала, подключенные к суммирующей точке операционного усилителя. Для НЧ-фильтра весовые коэффициенты должны быть пропорциональны (sin x)/x; обратите внимание, поскольку весовые коэффициенты могут быть обоих знаков, потребуется инвертирование некоторых уровней. Так как в этой схеме не используются конденсаторы, выходной сигнал будет состоять из набора дискретных уровней выходного напряжения.

Используя весовую функция для большого числа разрядов последовательности, можно улучшить приближение к гауссову шуму. Более того, в этом случае аналоговый выходной сигнал становится фактически непрерывным сигналом. По этим причинам желательно использовать как можно больше выходов регистра сдвига, используя в случае необходимости дополнительные ступени регистра сдвига, включенные в обратную связь с вентилем ИСКЛЮЧАЮЩЕЕ ИЛИ. Как и ранее, для задания стабильных цифровых уровней напряжения следует использовать резисторную «подвеску» к питанию или КМОП-ключи (для этих целей КМОП-логика является идеальным решением, поскольку выходы при этом точно соответствуют U_CC и земле).

Схема, показанная на рис. 9.90, генерирует псевдослучайный аналоговый шум, полосу которого можно менять с использованием рассмотренного способа в огромном диапазоне.

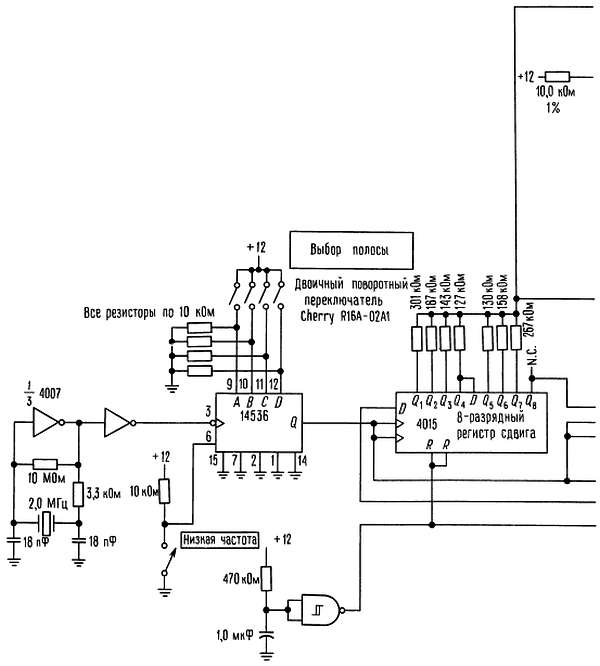
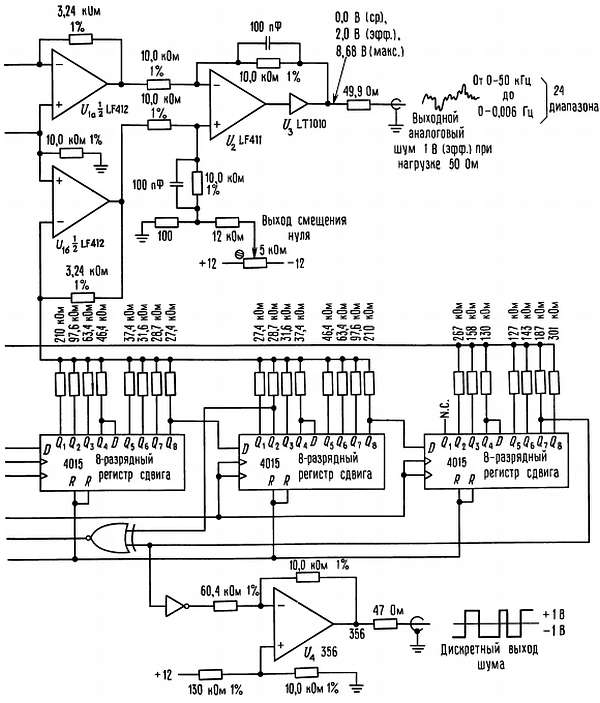
Рис. 9.90. Лабораторный генератор шума с широким частотным диапазоном.

Сигнал кварцевого генератора с частотой 2,0 МГц поступает на 24-разрядный программируемый делитель 14536, который формирует тактовую частоту от 1,0 МГц до 0,12 Гц с коэффициентом деления кратным 2. 32-разрядный регистр сдвига охвачен обратной связью от 31- и 18-го разрядов и генерирует последовательность максимальной длины с миллиардом состояний (на максимальной тактовой частоте полный цикл регистра проходит за полчаса). Здесь мы использовали взвешенное суммирование с функцией (sin x)/x на 32 последовательных разрядах последовательности. Элементы Y₁ и Y₂ усиливают инвертированные и неинвертированные выходы соответственно и запускают дифференциальный усилитель Y₃. Коэффициенты усиления выбираются таким образом, чтобы сформировать на 50-омной нагрузке напряжение 1,0 В ср. кв. без постоянной составляющей (2,0 В ср. кв. на холостом ходу). Обратите внимание на то, что эта амплитуда шума не зависит от тактовой частоты, т. е. от общей полосы. Такой цифровой фильтр имеет частоту среза на 0,05 f_такт и формирует спектр белого шума от полосы постоянный ток ÷ 50 кГц (максимальная тактовая частота) до полосы постоянный ток ÷ 0,006 Гц (минимальная тактовая частота) на 24 диапазонах. Схема вырабатывает выходной сигнал от +1,0 до -1,0 В. Относительно этой схемы можно сделать несколько важных замечаний.

Обратите внимание на то, что в этой схеме в обратной связи используется инвертирующий вентиль ИСКЛЮЧАЮЩЕЕ ИЛИ, поэтому инициализацию регистра можно осуществить простым обнулением. Использование инверсии входных последовательных сигналов исключает состояние «все единицы» (а не «все нули» как при использовании обычного вентиля ИСКЛЮЧАЮЩЕЕ ИЛИ), но все другие свойства остаются в силе.

Взвешенное суммирование конечного числа битов не может сформировать настоящий гауссов шум из-за ограничения по амплитуде пика. Можно показать, что выходная амплитуда пика (на 50 Ом) составляет ±4,34 В, что дает коэффициент формы 4,34. Эти цифры имеют важное значение, поскольку для того, чтобы исключить эффект ограничения, коэффициент усиления Y₁ необходимо с помощью Y₂ поддерживать достаточно низким. Внимательно приглядитесь к методам, используемым для формирования выходных сигналов с нулевой постоянной составляющей из уровней КМОП со средним значением +6,0 В (низкий уровень — 0 В, высокий — +12 В).

Описанный метод цифровой низкочастотной фильтрации последовательностей максимальной длины используется во многих коммерческих генераторах шума.

9.37. Краткое заключение

Несколько заключительных замечаний относительно последовательностей, генерируемых регистрами сдвига, как источников аналогового шума. На основании трех перечисленных ранее свойств регистров максимальной длины вы, возможно, склонны заключить, что выходная последовательность «чересчур случайна» в том смысле, что она имеет точное число серий заданной длины и т. п. Настоящая случайная машина для подбрасывания монеты не генерировала бы на единицу больше «орлов», чем «решек», а ее автокорреляционная функция не была бы абсолютно плоской для конечной последовательности. Посмотрите на это с другой стороны. Если бы вы использовали единицы и нули, вырабатываемые регистром сдвига, для управления случайным блужданием, двигаясь вперед на один шаг при получении единицы и назад на один шаг при получении нуля, то оказались бы на расстоянии ровно в один шаг от начальной точки после того, как регистр пройдет весь цикл. Этот результат уж никак нельзя назвать случайным!

Вместе с тем упомянутые свойства регистра сдвига верны только для всей последовательности из 2ⁿ — 1 бит, взятой как одно целое. Если вы используете фрагмент полной битовой последовательности, то его свойства будут довольно точно аппроксимировать случайный автомат для подбрасывания монеты. Представьте себе аналогичный процесс — извлечение красных и синих шаров наугад из урны, в которую вначале помещены К шаров (половина красных, половина синих). Если вы вытаскиваете шары без возвращения, то сначала вы рассчитываете получить почти случайную статистику. По мере убывания шаров в урне статистика изменяется за счет того, что общее число красных и синих шаров должно оставаться тем же самым.

Представление о том, как это происходит, можно получить, вновь вернувшись к случайному блужданию. Если предположить, что единственным «неслучайным» свойством последовательности является точное равенство «1» и «0» (не обращая внимание на одну лишнюю «1»), то можно показать, что описанное случайное блуждание после r вытаскиваний из общей «популяции» К/2 единиц и К/2 нулей приведет к среднему расстоянию от начальной точки, равному

Х = [r(К — r)/(К — 1)]^1/2.

(Этим выражением мы обязаны Ε. М. Purcell.) Поскольку при полностью случайном блуждании X равно корню квадратному из r, коэффициент (К — r /(К — 1) отражает влияние конечных содержимых урны. Пока r << К, случайность блуждания чуть-чуть отличается от случая абсолютно случайного блуждания, и генератор псевдослучайной последовательности практически неотличим от реального автомата. Мы проверили это на нескольких тысячах случайных блужданий под управлением ПСП (каждое в несколько тысяч шагов) и обнаружили идеальную случайность по этому простому критерию.

Тот факт, что генераторы ПСП выдерживают этот тест, разумеется, не гарантирует, что они будут удовлетворять и более сложным тестам на случайность, например тестам на корреляцию более высокого порядка. Такие корреляционные зависимости также оказывают влияние на свойства аналогового шума, генерируемого путем фильтрации ПСП. Несмотря на то что амплитуда шума имеет гауссово распределение, возможно наличие корреляции амплитуд более высокого порядка, не свойственной настоящему случайному шуму. По этому поводу сейчас принято считать, что чем больше отводов участвует в обратной связи (предпочтительно порядка m/2), тем «лучше» шумовые свойства (при использовании для формирования последовательных входов дерева четности на элементах ИСКЛЮЧАЮЩЕЕ ИЛИ).

Те, кто проектирует генераторы шумов, должны познакомиться со сдвиговым регистром переменной длины в КМОП-логике 4557 (от 1 до 64 разрядов); конечно, вы должны использовать его в сочетании с регистром с параллельным выходом (типа `4015 или `164) для того, чтобы обеспечить n отводов.

В разд. 7.20 обсуждается вопрос о шумах и приводится пример генератора «розового» шума на ИМС регистра максимальной длины ММ5437.

9.38. Цифровые фильтры

Последний пример затронул интересную тему цифровой фильтрации, в данном случае формирование НЧ-сигнала путем взвешенного суммирования 32 значений псевдослучайной последовательности, каждое из которых соответствует уровню напряжения 0 или +12 В. На вход такого «фильтра» поступают сигналы, которые могут иметь только два уровня напряжения. Вообще говоря, то же самое можно сделать с аналоговым сигналом на входе, образуя взвешенную сумму его значений (x_i), распределенных во времени через равные интервалы

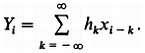
Здесь x_i являются дискретными выборками из входного сигнала, h_k — весовые коэффициенты, а y_i - значения выходного сигнала. В реальных условиях цифровой фильтр будет суммировать только конечное множество входных значений, как, например, в генераторе шума, где было использовано 32 члена. На рис. 9.91 схематично показано, как это происходит.

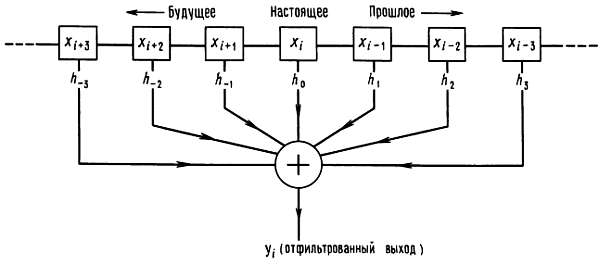
Рис. 9.91. Нерекурсивный цифровой фильтр.

Заметьте, что такой фильтр может обладать интересным свойством симметричности во времени, т. е. усреднением прошлого и будущего для того, чтобы сформировать текущее значение выхода.

Разумеется, реальные аналоговые фильтры умеют лишь смотреть в прошлое и соответствуют цифровым фильтрам с ненулевыми весовыми коэффициентами только при k >= 0.

Частотная характеристика симметричного фильтра. Можно показать, что частотная характеристика симметричного фильтра (h_k = h_-k) имеет вид

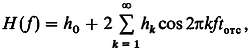
где t_отс — время между выборками (отсчетами). Нетрудно заметить, что h_k представляют собой коэффициенты разложения в ряд Фурье требуемой частотной характеристики. Это объясняет, почему в случае представленной ранее схемы генератора весовые коэффициенты были выбраны в соответствии с функцией (sin x)/x: они являются компонентами Фурье заграждающего НЧ-фильтра. В таких симметричных фильтрах фазовый сдвиг на любой частоте либо равен 0, либо 180°.

Рекурсивные фильтры. Можно получить интересный класс цифровых фильтров, если на вход фильтра в дополнение к внешнему входному сигналу подать собственный выходной сигнал фильтра. Такой фильтр можно рассматривать как фильтр с обратной связью. Он имеет причудливое название рекурсивный фильтр (или с бесконечной импульсной характеристикой) в противоположность рассмотренному выше нерекурсивному (с конечной импульсной характеристикой) фильтру. Можно, например, сформировать выходной сигнал в соответствии со следующим выражением:

y_i = Ay_i-1 + (1 — A)x_i

Это соответствует низкочастотной характеристике, эквивалентной той, которой обладает простой низкочастотный RC-фильтр

А = е^-t_отс/RC

где t_отс - интервал времени между последовательными выборками х_i из входного сигнала. Эта ситуация, конечно, не является идентичной ситуации с аналоговым низкочастотным фильтром, работающим с аналоговым сигналом, по причине дискретной природы отсчетов.

Пример НЧ-фильтра. В качестве числового примера предположим, что вам требуется отфильтровать ряд числовых значений, соответствующих сигналу с затуханием 3 дБ на частоте f_{3 дб} = 1/20t_отс. Таким образом, постоянная времени соответствует интервалу времени 20 последовательных отсчетов. В этом случае А = 0,95123, а выходной сигнал определяется по выражению y_i = 0,95123y_i-1 + 0,04877х_i. С увеличением постоянной времени относительно времени между отсчетами t_отс приближение к реальному НЧ-фильтру улучшается.

Для обработки данных уже представленных в виде дискретных отсчетов, как, например, массив данных в компьютере, вы, возможно, предпочтете использовать такой фильтр. Рекурсивный фильтр при этом будет реализовываться с помощью однократного прохода по данным с тривиальной арифметической обработкой. Программа НЧ-фильтра на языке Фортран будет выглядеть следующим образом:

A = exp(-TS/TC)

В = 1. — А

DO 10I = 2,N

10X(I) = A*X(I — 1) + B*X(I),

где X — матрица данных, TS — интервал времени между отсчетами (т. е. TS = 1/t_отс), а ТС — выбранная постоянная времени фильтра. Эта маленькая программа осуществляет фильтрацию на месте, т. е. она заменяет первоначальные данные отфильтрованными. Можно, конечно, создавать из отфильтрованных данных отдельный массив.

НЧ-фильтр с коммутацией. Такой же фильтр можно построить аппаратным путем, используя схему, показанную на рис. 9.92.

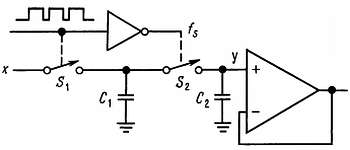
Рис. 9.92. Рекурсивный фильтр на коммутируемых конденсаторах.

Ключи на полевых транзисторах S₁ и S₂ коммутируются с некоторой тактовой частотой, периодически заряжая конденсатор С₁ до входного напряжения и затем передавая его заряд на конденсатор С₂. Если С₂ имеет напряжение U₂, а С₁ заряжается до входного уровня U₁, то при подключении С₁ к С₂ напряжение на обоих конденсаторах будет определяться соотношением U = (С₁U₁ + С₂U₂)/(C₁ + С₂), что эквивалентно рассмотренному ранее рекурсивному фильтру при

у_i = С₂/(C₁ + C₂)у_i-1 + С₁/(C₁ + C₂)x_i.

Приравнивая эти коэффициенты к заданному ранее значению А, получим

f_{3 дB} = (1/2π)f_отсln(C₁ + C₂)/C₂.

_{Упражнение 9.8. Покажите, что этот результат правилен.}

Этот фильтр практичен во всех отношениях и обладает одной привлекательной особенностью — электронной настройкой посредством тактовой частоты f_отс. В обычных схемах используются КМОП-ключи, а емкость С₁ берется много больше С₂. Поэтому сигнал переключения должен быть несимметричным и большую часть времени тратить на замыкание S₁.

Приведенная схема представляет собой простой пример фильтра с коммутацией; в этот класс фильтров входят фильтры, выполненные на матрицах коммутируемых конденсаторов. Они имеют периодическую частотную характеристику, что делает их удобными для использования в качестве гребенчатых и узкополосных режекторных фильтров.

Для всех фильтров классического типа (Баттерворта, Чебышева и т. п.) можно построить их приближенные дискретные аналоги в форме ВЧ, НЧ, полосовых и заграждающих фильтров, как симметричных во времени, так и с истинным временем запаздывания. Такие фильтры очень удобны при обработке квантованных данных, перед которыми, безусловно, большое будущее.

В настоящее время выпускают большое число недорогих ИМС фильтров с коммутируемыми конденсаторами. ИМС MF4 фирмы National, например, является 4-звенным НЧ-фильтром Баттерворта, размещенным в корпусе мини-DIP; он не требует внешних компонентов и работает от одного источника питания с напряжением от +5 до +14 В. Частота среза фильтра (0,1 Гц мин. и 20 кГЦ макс.) устанавливается с помощью внешней тактовой частоты f_такт = 100f_{3 дB}. ИМС MF5 и MF10 («универсальные фильтры с коммутируемыми конденсаторами») работают несколько иначе. С помощью внешних резисторов устанавливаются тип фильтра (ВЧ, НЧ, полосовой, заграждающий) и характеристика фильтра (Баттерворта, Чебышева и т. п.), а с помощью тактовой частоты, как и раньше, устанавливается частота среза. Другими изготовителями фильтров с коммутируемыми конденсаторами являются фирмы American Microsystems (AMI), Linear Technology (LTC) и Reticon. Фирма LTC как всегда использовала несколько хитроумных приемов для улучшения технических характеристик. Ее фильтры LTC1062 и МАХ280 похожи на MF4, но являются 5-звенными и имеют нулевую ошибку на постоянном токе! Последнее свойство реализовано путем размещения фильтра вне пути постоянного тока (рис. 9.94).

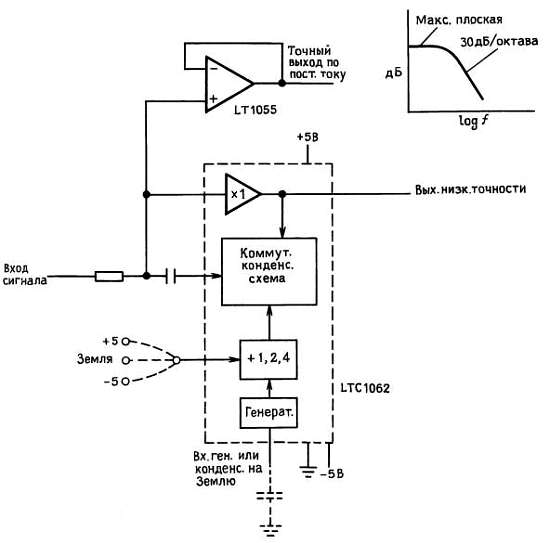
Рис. 9.94. Цифровой НЧ-фильтр с малым сдвигом по постоянному току.

Гибкие фильтры серии МАХ260 допускают управление важными параметрами фильтра от микропроцессора. Вообще говоря, такие фильтры с коммутируемыми конденсаторами работают только на верхнем конце звукового диапазона. В них также наблюдается существенное проникновение тактовой частоты на выход обычно в пределах 10–25 мВ. Это ограничивает их динамический диапазон в тех применениях, где тактовая частота находится внутри полосы пропускания (например, ВЧ-фильтры). Они могут иметь значительный шум, ограничивающий динамический диапазон до 80 дБ и менее (сравните со 140 дБ и выше для хорошего операционного усилителя). С другой (положительной) стороны, фильтры на коммутируемых конденсаторах просты в применении и позволяют осуществлять эффективную настройку (с помощью тактовой частоты). Фильтры такого типа широко используют в модемах (при передаче данных по телефонным линиям) и в других областях связи. См. разд. 5.11.

Формирование синусоидальных колебаний цифровым способом. С нерекурсивной цифровой фильтрацией связан интересный способ синтеза синусоидальных колебаний с использованием взвешенных сумм сигналов с выходов счетчика Джонсона (кольцевой счетчик с коэффициентом пересчета, вдвое превышающим число разрядов). Схема на рис. 9.93 показывает способ реализации такого генератора.

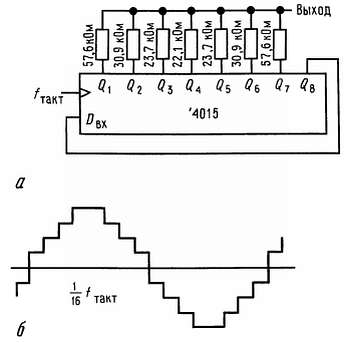
Рис. 9.93. Цифровой генератор синусоидальных сигналов.

ИМС 4015 представляет собой 8-разрядный регистр сдвига с параллельным выходом. Подавая на вход инвертированный сигнал с последнего разряда, можно организовать счетчик Джонсона, который будет проходить через 16 состояний (в общем случае 2n состояний для n-разрядного регистра сдвига). Начиная с состояния «все нули», происходит заполнение счетчика слева направо «1» (марш «1») до полного заполнения всеми единицами, затем начинается марш «0» и т. д. Показанное на рисунке взвешивание формирует 8-уровневое приближение к синусоидальному колебанию с частотой, равной 1/16 тактовой частоты, и с первым ненулевым членом искажения на 15-й гармонике, имеющей затухание 24 дБ.