Комбинационная логика

Как мы обсуждали ранее в разд. 8.04, цифровые логические схемы разделяются на комбинационные и последовательностные (последовательные). Комбинационные схемы — это такие логические устройства, в которых состояние выхода зависит только от текущего состояния их выходов в некотором предопределенном виде. Выходное состояние последовательностной схемы определяется как состояние входов на данный момент, так и ее предыдущим состоянием. Комбинационные схемы могут быть построены с применением одних лишь вентилей, в то время как последовательностные схемы требуют наличия памяти в какой-либо форме (триггер). В последующих разделах мы рассмотрим возможности комбинационной логики, после чего отправимся в беспокойный мир последовательностных схем.

8.12. Логические тождества

Любое обсуждение комбинационной логики будет неполным, если мы не рассмотрим логические тождества, представленные в табл. 8.3. Из этих соотношений большинство очевидны, а два последних составляют теорему Моргана, наиболее важную для построения схем.

Таблица 8.3. Логические тождества

АВС = (АВ)С = А(ВС)

АВ = ВА

АА = А

А1 = А

А0 = 0

А(В + С) = АВ + АС

А + АВ = А

A + BC = (A + B)(A + С)

A + B + C = (A + B) + C = A + (B + С)

A + В = В + А

А + А = А

А + 1 = 1

А + 0 = А

1' = 0

0' = 1

А + А' = 1

АА' = 0

(А')' = А

А + А'В = А + В

(А + В)' = А'В'

(АВ)' = А' + В'

Пример: вентиль Исключающее ИЛИ.

На следующем примере проиллюстрируем использование логических тождеств: попробуем построить схему Исключающее ИЛИ с помощью обычных вентилей. Таблица истинности для Исключающего ИЛИ представлена на рис. 8.24. Изучив ее и поняв, что 1 на выходе существует только тогда, когда (А, В) = (0, 1) или (1, 0), мы можем написать А  В = А¯В + АВ¯

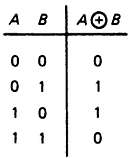
Рис. 8.24. Таблица истинности вентиля Исключающее ИЛИ.

Соответствующая схемная реализация представлена на рис. 8.25.

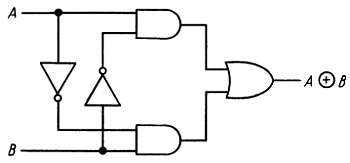
Рис. 8.25. Реализация вентиля Исключающее ИЛИ.

Однако эта реализация не является единственной. Используя логические тождества, мы находим, что

Α  В = АА¯ + АВ¯ + ВА¯ + ВВ¯ (АА¯ = ВВ¯ = 0)

= А(А¯ + В¯) + В(А¯ + В¯)

= А(А¯В¯) + В(В¯А) = (А + В)(А¯В¯)

(На первом шаге мы прибавили две величины, равные нулю, а на третьем применили теорему Моргана). Схемная реализация для этого случая показана на рис. 8.26.

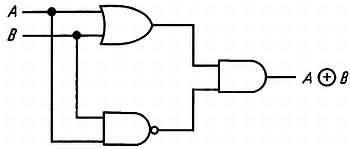
Рис. 8.26. Реализация вентиля Исключающее ИЛИ.

Существуют и другие способы построения схемы Исключающее ИЛИ. Рассмотрим следующие упражнения:

_{Упражнение 8.11. Покажите, что}

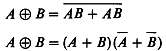
_{с помощью логических преобразований. В справедливости этих соотношений легко убедиться, просмотрев таблицу истинности.}

_{Упражнение 8.12. Чему равны следующие соотношения:}

_{а) 0·1, б) 0 + 1, в) 1·1, г) 1 + 1, д) А(А + В), е) А(А' + В), ж) Α  А, з) Α  Α'.}

8.13. Минимизация и карты Карно

Поскольку логическую функцию, даже такую простую, как Исключающее ИЛИ, можно реализовать различными способами, часто бывает нужно найти для нее самое простое решение, или, возможно, наиболее удобное схемное решение. Над этой проблемой бились многие светлые умы и в настоящее время существует несколько способов ее разрешения, включая алгебраические методы, реализуемые с помощью ЭВМ. При числе входов, не превышающем четырех, наилучшим методом является составление карты Карно. Этот метод позволяет также найти логическое выражение (если оно заранее неизвестно) по таблице истинности. Проиллюстрируем этот метод с помощью примера.

Предположим, что требуется построить схему для мажоритарного подсчета голосов при баллотировке. Будем считать, что имеются три входа, работающие в положительной логике (на любом из них может быть 1 или 0) и выход (0 или 1). Выход равен 1, если 1 присутствует не менее чем на двух входах.

Шаг 1. Составим таблицу истинности

Здесь должны быть представлены все возможные сочетания и соответствующие им состояния выхода (или выходов). В том случае, когда состояние входа не оказывает влияния на выход, ставится X (любое значение).

Шаг 2. Составим карту Карно. Она представляет собой нечто очень близкое к таблице истинности, но содержит переменные, которые расположены по двум осям. Переменные должны быть расположены таким образом, чтобы при переходе от каждого квадрата к соседнему менялось бы состояние только одного входа (рис. 8.27).

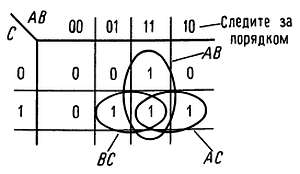
Рис. 8.27. Карта Карно.

Шаг 3. Отметим на карте группы, содержащие 1 (можно также использовать и группы, содержащие 0). Три овала на рис. 8.27 определяют логические выражения АВ, АС и ВС. Далее получим требуемую функцию

Q = АВ + АС + ВС,

схемная реализация ее показана на рис. 8.28.

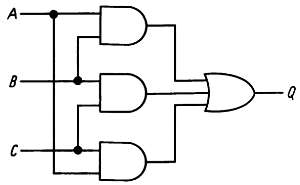
Рис. 8.28.

Этот результат кажется очевидным, когда он уже получен. Можно было бы составить выражение для нулей и вместо этого получить

Q = А'В' + А'С + В'С.

Это выражение может оказаться полезным для случая, когда в каких-либо точках схемы имеются дополнения А', В' и С.

Некоторые комментарии к картам Карно.

1. Ищите группы, содержащие 2, 4, 8 и т. д. квадратов. Они имеют простые логические выражения.

2. Логика будет тем проще, чем крупнее блок вы опишете.

3. Состыкуйте края карты Карно. Например, карта на рис. 8.29 описывается выражением Q = В'С.

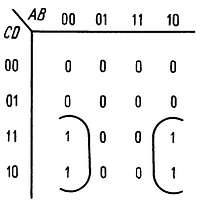
Рис. 8.29.

4. Блок «единиц», содержащий один или два «нуля», лучше всего описывается с помощью группировки, показанной на рис. 8.30. Этому блоку соответствует логическое выражение Q = A(BCD)'.

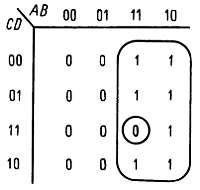
Рис. 8.30.

5. Места, содержащие X (любое значение), представляют собой «карт-бланш». Записывайте в них «нули» или «единицы» так, чтобы можно было получить простейшую логику.

6. Карта Карно может и не привести к лучшему решению. Иногда более сложное логическое выражение имеет более простую схемную реализацию, например в случае, когда некоторые члены выражения уже сформированы схемой в виде логических сигналов, которые можно использовать в качестве входных. Кроме того, реализации Исключающего ИЛИ не очевидны из карты Карно. Наконец, при выборе логической структуры схемы определенную роль играют ограничения, связанные с конструкцией ИМС (например, когда в одном корпусе содержатся четыре 2-входовых вентиля). Когда используются такие программируемые логические устройства как ПМЛ для конструирования логических функций, внутренняя структура (программируемые вентили И и фиксированные вентили ИЛИ) сдерживает реализацию, которая могла бы быть применена.

_{Упражнение 8.13. Нарисуйте карту Карно для логики, которая позволит определить, является ли 3-разрядное двоичное число «главным», считая при этом, что главными не являются числа 0, 1 и 2. Дайте схемную реализацию на 2-входовых вентилях.}

_{Упражнение 8.14. Найдите логическое выражение, с помощью которого можно было бы умножить два 2-разрядных двоичных числа и получить 4-разрядный результат. Рекомендации: для каждого выходного бита пользуйтесь отдельными картами Карно.}

8.14. Комбинационные функциональные схемы, реализованные на стандартных ИМС

С помощью карт Карно можно построить логику, чтобы выполнять достаточно сложные функции, такие, как, например, двоичное сложение и сравнение величин, контроль по паритету, мультиплексирование (выбор одного из нескольких входов, который определяется двоичным адресом) и т. п. В реальности сложные функции, которые используются наиболее часто, реализуются в виде функциональных ИМС средней степени интеграции (до 100 вентилей в корпусе). Хотя в состав многих из этих СИС входят триггеры, которые мы скоро будем рассматривать, большинство из них выполняют чисто комбинационные функции и состоят целиком из одних вентилей. Давайте посмотрим, «какие звери населяют зоопарк, именуемый комбинационные интегральные схемы средней степени интеграции.»

Счетверенная 2-входовая схема выборки. Весьма полезным устройством является счетверенная 2-входовая схема выборки. Она фактически представляет собой 4-полюсный двухпозиционный переключатель логических сигналов. Основная идея такого переключателя иллюстрируется рис. 8.31.

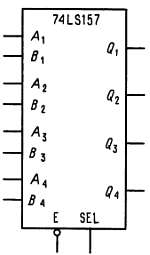
Рис. 8.31. Счетверенный 2-входовый селектор.

Когда вход ВЫБОР (SELECT-SEL на рисунке) имеет низкий уровень, сигналы на выходах Q поступают с соответствующих входов А, при высоком уровне на входе ВЫБОР — со входов В. Когда высокий уровень действует на входе РАЗРЕШЕНИЕ (ENABLE-E на рисунке), все выходы устройства принудительно устанавливаются в состояние низкого уровня. Несколько позже мы рассмотрим эту важную идею более подробно, а сейчас приведем лишь таблицу истинности, в которой X означает, что состояние данного входа не имеет значения, В — высокий уровень, Η — низкий уровень.

Схема на рис. 8.31 и ее таблица истинности соответствуют схеме `157. Та же самая функция реализуется также с инверсным выходом (`158) и с выходом на 3 состояния (прямые выходы; `257; инверсные: `258).

_{Упражнение 8.15. Покажите, как с помощью вентилей И-ИЛИ-НЕ построить 2-входовую схему выборки.}

Хотя в некоторых случаях функцию выборки можно реализовать с помощью механического переключателя, тем не менее по ряду причин предпочтительнее использовать вентили. Вентильная схема обладает следующими преимуществами: а) она дешевле; б) коммутация всех каналов производится быстро и одновременно; в) с помощью логических сигналов, сформированных в устройстве, можно производить переключение практически мгновенно; г) даже тогда, когда управление выборкой осуществляется от переключателя, расположенного на передней панели устройства, для того чтобы избежать воздействия помехи и снижений уровней за счет влияния емкостей, логические сигналы лучше не пропускать через кабели и переключатели. Так как избираемый вентиль отпирается уровнем постоянного напряжения, логические сигналы управления могут быть взяты с той же платы, на которой он расположен. Это позволяет сократить внешние связи (достаточно одной линии с нагрузкой, коммутируемой на землю с помощью однополюсного тумблера). Такой способ управления логической схемой с помощью внешних уровней постоянного напряжения называют «холодной коммутацией». Он оказывается более предпочтительным, чем непосредственное управление сигналами от ключей, потенциометров и т. п. Кроме прочих преимуществ холодная коммутация позволяет вести управляющие линии, шунтированные конденсаторами, подавляя тем самым взаимные наводки, в то время как сигнальные линии в общем случае шунтировать конденсаторами нельзя. Некоторые примеры холодной коммутации нам еще встретятся в дальнейшем.

Передающие вентили. Как уже указывалось в разд. 3.11 и 3.12, с помощью элементов КМОП можно построить «передающий вентиль». Это — два параллельно включенных комплементарных ключа на полевых МОП-транзисторах, через которые входной (аналоговый) сигнал, лежащий в пределах от 0 до U_СС, может либо непосредственно подаваться на выход через низкое сопротивление (несколько сотен омов), либо отрываться (выходное сопротивление фактически равно бесконечности). Как вы, наверное, помните, такие устройства являются двунаправленными и для них не имеет значения, какой из выходов используется в качестве входа, а какой в качестве выхода.

Передающие вентили прекрасно работают с цифровыми уровнями КМОП и широко применяются в КМОП-схемах. На рис. 8.32 показана структурная схема счетверенного двухстороннего КМОП-ключа типа 4066. Каждый ключ имеет индивидуальный управляющий вход, высокий уровень на котором замыкает ключ, а низкий — размыкает.

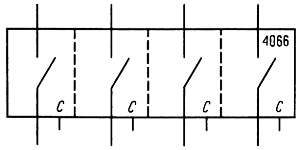
Рис. 8.32. Счетверенный двусторонний ключ.

Отметим, что передающие вентили являются просто ключами, и поэтому не обладают способностью к разветвлению по выходу, т. е. они просто пропускают входной логический уровень, не обеспечивая дополнительную нагрузочную способность без дополнительной возможности усиления. С помощью передающих вентилей можно построить схемы выборки на 2 и более входов для цифровых уровней КМОП и аналоговых сигналов. Связку передающих вентилей можно использовать для того, чтобы производить выбор одного из нескольких входов (вырабатывая управляющие сигналы с помощью дешифратора, как будет показано ниже).

Эта логическая функция настолько широко используется, что получила официальное название «мультиплексора», который будет рассмотрен в следующем разделе.

_{Упражнение 8.16. Покажите, как с помощью передающих вентилей построить схему выборки на два входа. Здесь нужно использовать инвертор.}

Мультиплексоры. Вентиль выборки на два входа известен также под названием 2-входового мультиплексора. Промышленностью выпускаются также мультиплексоры на 4, 8 и 16 входов (устройства на 4 входа выпускаются сдвоенными, т. е. по 2 в одном корпусе). Двоичный адрес служит для выбора входа, сигнал с которого должен поступать на выход. Например, мультиплексор, имеющий 8 информационных входов, использует для адресации к ним 3-разрядный адресный вход. Это показано на рис. 8.33, где представлен цифровой мультиплексор типа `151.

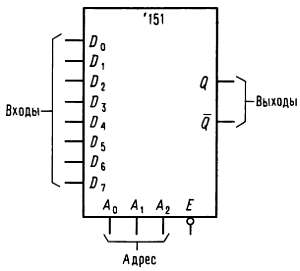
Рис. 8.33. 8-входовый мультиплексор.

Он имеет стробирующий (или разрешающий) вход Е, работающий в отрицательной логике, а также прямой и инверсный выходы. Если устройство закрыто (на входе Ε действует высокий уровень), выход Q будет иметь низкий уровень, a Q' — высокий независимо от состояния адресных и информационных входов.

В семействе КМОП имеются два типа мультиплексоров. Первый применяется только для работы с цифровыми сигналами, имеет входной порог и регенерирует на выходе «чистые» уровни, которые соответствуют входному состоянию. Таким же образом работают все функциональные элементы ТТЛ. Примером является микросхема `153 — ТТЛ-мультиплексор. К другому типу устройств относятся аналоговые и двунаправленные КМОП мультиплексоры, которые фактически представляют собой набор передающих вентилей, КМОП-мультиплексоры 4051 и 4053 работают таким образом (помните, что логика, выполненная из передающих вентилей, не может разветвляться). Так как передающие вентили являются двунаправленными, эти мультиплексоры могут использоваться в качестве «демультиплексоров или дешифраторов», которые мы рассмотрим в следующем разделе.

_{Упражнение 8.17. Покажите, как построить мультиплексор на 4 входа, используя а) обычные вентили, б) вентили с тремя состояниями и в) передающие вентили. При каких обстоятельствах будет предпочтительным вариант в)?}

Иногда при разработке логических устройств может оказаться, что потребуется производить набор из большего числа входов, чем имеются в мультиплексоре. Этот вопрос относится к общей задаче расширения микросхем, которое заключается в использовании нескольких микросхем с небольшими индивидуальными возможностями, и применяется для построения дешифраторов, памяти, регистров сдвига, арифметически-логических и других устройств. Как видно из рис. 8.34, расширение выполняется очень просто. Здесь показано, как имея два мультиплексора на 8 входов 74LS51 построить мультиплексор на 16 входов.

Рис. 8.34. Наращивание мультиплексора.

Конечно, в схемах имеется дополнительный адресный бит, который вы используете для выбора одного устройства или другого. На невыбранном мультиплексоре `151 выход Q поддерживается на низком уровне, что позволяет произвести объединение через вентиль ИЛИ. Если выходы имеют три состояния, то расширение производится еще проще: для этого достаточно непосредственно объединить выходы.

Демультиплексоры и дешифраторы. Входной сигнал принимается демультиплексором и направляется им на один из нескольких выходов в соответствии с двоичным кодом, действующим на адресных входах. Остальные выходы в этом случае находятся либо в неактивном состоянии, либо в состоянии разомкнутой цепи. Аналогично работает и дешифратор. Единственное отличие состоит в том, что на входы подается только адрес, возбуждающий один из n возможных выходов. На рис. 8.35 показан такой пример.

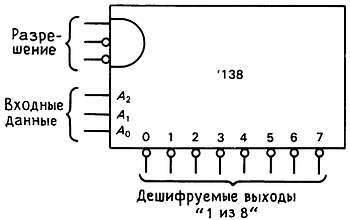
Рис. 8.35. Дешифратор «1 из 8».

Дешифратор `138 — "1 из 8" имеет низкий уровень на выходе, который соответствует входному 3-разрядному коду (адресу), а на остальных выходах — высокий уровень. В частности этот дешифратор имеет три входа разрешение, все из которых должны быть активны (два — низкого и один — высокого уровня), иначе все выходы имеют высокий уровень. Основное применение дешифратора — заставить происходить различные события, которые зависят от состояния «счетчика», который управляет этим (скоро об этом тоже поговорим подробно).

Дешифраторы обычно используются при сопряжении с микропроцессором, когда необходимо выполнить различные действия в зависимости от адреса. Мы будем рассматривать это детально в гл. 10.

Другим применением общего использования дешифратора является организация (разрешение) последовательности действий, согласно достигнутого адреса, заданного выходом двоичного счетчика (разд. 8.25). В заключение, о «брате» схемы `138 — схеме `139, которая представляет сдвоенный дешифратор "1 из 4" с раздельным одиночным разрешением по низкому уровню. На рис. 8.36 показано, как использовать два дешифратора `1 из 8' типа `138 для получения дешифратора "1 из 16". Как видно из рисунка, при этом не требуются внешние элементы, поскольку схема `138 имеет входы разрешения обеих полярностей (низкого и высокого уровней).

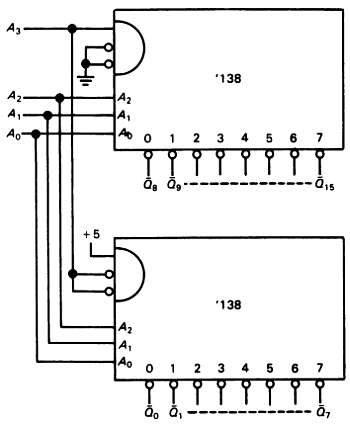
Рис. 8.36. Наращивание дешифратора.

_{Упражнение 8.18. Большое расширение: постройте дешифратор "1 из 64" на девяти устройствах `138. Подсказка: используйте один из них для разрешения подключения других.}

В КМОП-логике мультиплексоры, которые используют передающие вентили, также являются демультиплексорами, поскольку передающие вентили являются двунаправленными. Когда они используются таким образом, важно сознавать, что выходы, которые не выбраны, отключены. Нагрузочный резистор, или эквивалентный ему, должны быть использованы для обеспечения правильного функционирования логики с такими выходами (те же самые требования, что и с ТТЛ-вентилями с открытым коллектором).

Существует другой тип дешифраторов, который обычно входит в состав всех логических семейств. Примером такого дешифратора служит преобразователь двоично-десятичного кода в семисегментный с формирователями для управления цифровым индикатором `47. Эта схема в соответствии с двоично-десятичным кодом, действующим на входе, формирует сигналы на всех выходных линиях, связанных со входами семисегментного цифрового индикатора, воспроизводящего десятичный символ. Устройство такого типа фактически является преобразователем кодов, но в обычной практике используется название дешифратор. В табл. 8.6 в конце главы представлено большинство применяемых дешифраторов.

_{Упражнение 8.19. Используя вентили, постройте преобразователи двоично-десятичного кода в десятичный ("1 из 10").}

Приоритетный шифратор. Приоритетный шифратор формирует на выходе двоичный код, соответствующий входу с наивысшим номером (приоритетом), который возбуждается. Наиболее часто эта схема используется в аналого-цифровых преобразователях с параллельным преобразованием (см. следующую главу) и в проектировании микропроцессорных систем. Примерами устройств такого типа являются схема `148 — 8-входовый (3 выходных разряда) приоритетный шифратор и схема `147 — 10-входовый.

_{Упражнение 8.20. Спроектируйте простейший дешифратор, у которого 2-разрядный адрес на выходе будет указывать, какой из четырех входов имеет высокий уровень (все остальные входы должны иметь низкий уровень).}

Сумматоры и другие арифметические устройства. На рис. 8.37 изображен 4-разрядный полный сумматор. Он прибавляет 4-разрядное двоичное число А_i к 4-разрядному числу В_i и вырабатывает на выходе 4-разрядную сумму S_i плюс разряд переноса П_вых. Для суммирования больших величин сумматоры можно наращивать. Для этой цели предусмотрен вход П_вх, на который поступает выходной сигнал переноса от предыдущего (младшего) сумматора.

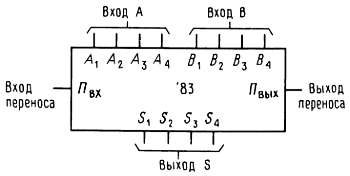
Рис. 8.37. 4-разрядный полный сумматор.

На рис. 8.38 показано, как строится схема для суммирования двух 8-разрядных двоичных чисел.

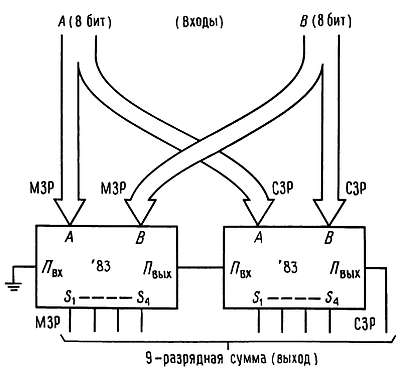
Рис. 8.38. Наращивание сумматора.

Часто в качестве сумматоров используются арифметико-логические устройства (АЛУ). Эти устройства фактически предназначены для выполнения целого ряда различных функций. В частности, 4-разрядная АЛУ `181 (с возможностью расширения для обработки слов большей длины) может выполнять сложение, вычитание, сдвиг двоичных разрядов, сравнение величин и некоторые другие функции. Время выполнения арифметических операций в сумматорах и АЛУ находится в пределах от наносекунд до десятков наносекунд в зависимости от типа логического семейства.

Интегральные умножители выпускаются в конфигурациях 8 бит x 8 бит или 16 бит x 16 бит. Разновидностью умножителей, которые в основном используются для цифровой обработки сигналов, являются так называемые умножители-накопители, которые накапливают сумму произведений. Они также выполняются в размерах 32x32 с 64-битовым произведением плюс несколько дополнительных бит для сохранения суммы от переполнения. Умножители-накопители и умножители выпускаются с временем 25–50 нс; у ЭСЛ-умножителей время меньше — 5 нс (тип.) для умножителей 16x16.

Другим арифметическим устройством, которое используется в цифровой обработке сигналов, является коррелятор, который сравнивает соответствующие биты двух цепочек битов, вычисляя число совпавших битов. Типовой интегральный коррелятор сравнивает два 64-разрядных, которые могут сдвигаться во внутренних регистрах сдвига. Какой-либо набор бит может игнорироваться («маскироваться») в корреляции. Типовые времена составляют 30 нс, т. е. лента бит может тактироваться с частотой 35 МГц, с разрешением 7 бит в корреляции для каждого такта. Вычисляется отклонение (как в цифровом фильтре с КИХ) вместо суммы (с переносом) попарносвязанных произведений двух цепочек целых чисел.

Типичные размеры — целые числа от 4 до 10 бит при длине от 3 до 8 слов (конечно, имеющие возможность расширения). Наиболее сложными арифметическими кристаллами являются процессоры с плавающей запятой, которые осуществляют сравнение, суммирование, умножение, вычисление тригонометрических функций, экспонент и корней. Обычно они используются совместно с определенными микропроцессорами и приспособлены для работы в стандарте, известном как IEED754, который определяет размеры слов (до 80 бит), формат и т. д. Примерами таких устройств (плюс основные микропроцессоры) являются схемы 8087 (80848), 80287 (80286), 80387 (80386) и 68881 (68020/30). Они имеют действительно ошеломляющую производительность в 10 Мегафлопс (миллион операций с плавающей запятой в секунду) или более.

Компараторы. На рис. 8.39 показан 4-разрядный компаратор чисел, который определяет относительные значения чисел А и В и вырабатывает на выходе сигналы результатов сравнения: А < В, А = В и А > В. Входы допускают наращивание для обработки чисел длиной более 4 бит.

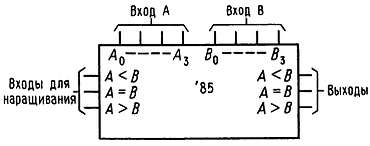
Рис. 8.39. Компаратор.

_{Упражнение 8.21. Сконструируйте компаратор, используя вентили «исключающее или», который будет сравнивать 4-разрядные числа А и В и определять, когда А = В.}

Схема формирования и контроля бита паритета. Это устройство предназначено для выработки паритетного бита, который добавляется к информационному «слову» при передаче (или записи) данных, а также для проверки правильности паритета при восстановлении этих данных. Паритет может быть четным или нечетным (при нечетном паритете для каждого символа общее число битов (разрядов), содержащих 1, нечетно). Например, формирователь паритета 1280 принимает 9-разрядное слово и в соответствии с состоянием управляющего входа вырабатывает на выходе четный или нечетный бит. Конструктивно схема представляет собой набор вентилей «исключающее или».

_{Упражнение 8.22. Подумайте, как сделать формирователь паритета, используя вентили «исключающее или».}

Программируемые логические устройства. Вы можете строить ваши собственные комбинационные (и даже последовательные) логические схемы на кристалле, используя ИС, которые содержат массив вентилей с программируемыми перемычками. Существуют несколько вариантов таких устройств, из которых наиболее популярными являются ПМЛ (программируемая матричная логика — PAL) и ПЛМ (программируемая логическая матрица — PLA). ПМЛ, в частности, стали крайне недорогими и гибкими устройствами, которые должны войти как часть инструмента каждого разработчика. Мы будем описывать комбинационные ПМЛ в следующем разделе.

Некоторые другие незнакомые функции. Существует много других комбинационных схем средней степени интеграции, представляющих несомненный интерес. Например, в семействе КМОП есть схема — «мажоритарная логика», которая говорит, что возбуждена большая часть входов. Имеется также двоично-десятичное устройство дополнения до 9, назначение которого не требует пояснений. Существует схема «барабан-сдвигатель», которая сдвигает входное число на n (задаваемое) разрядов и может наращиваться до любой длины.

8.15. Реализация произвольных таблиц истины

К счастью, большинство из проектов цифровых схем не состоит из стряпни безумных устройств на вентилях для реализации сложных логических функций. Однако временами, когда вам нужно связать несколько сложных таблиц истинности, число вентилей может стать слишком большим. Возникает вопрос, нельзя ли найти какой-то другой путь. Таких путей существует несколько. В этом разделе мы кратко рассмотрим, как использовать мультиплексоры и демультиплексоры для реализации произвольных таблиц истинности. Затем мы обсудим в общем более мощные методы, использующие программируемые логические кристаллы, в частности ПЗУ и ПЛМ.

Мультиплексоры в качестве реализаций обобщенных таблиц истинности. Нетрудно видеть, что n-входовый мультиплексор может быть использован для генерации любой таблицы истинности на n входов без применения каких-либо внешних компонентов, если просто на их входы подать соответствующие высокие и низкие уровни. Схема на рис. 8.40 говорит, является ли входное 3-разрядное двоичное число простым.

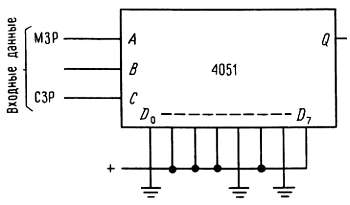
Рис. 8.40.

Не столь очевидно, что мультиплексор на n входов с помощью только одного инвертора может быть использован для генерации таблицы истинности на 2n входов. Например, рис. 8.41 показывает схему, которая определяет имеет или нет данный месяц года 31 день, где месяц (от 1 до 12) задается 4-битовым входом.

Хитрость в том, чтобы заметить, что для данного состояния адресных битов, прикладываемых к мультиплексору, выход (как функция оставшегося входного бита) должен быть равен H, L, А₀ или А'₀; соответственно вход мультиплексора связывается с логическим высоким, логическим низким, А или А'₀.

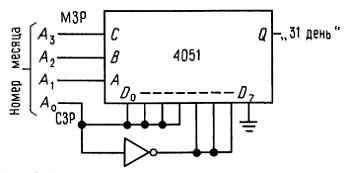
Рис. 8.41.

_{Упражнение 8.23. Схема на рис. 8.41. Составьте таблицу, показывающую, имеет ли данный месяц 31 день, с двоичной адресацией месяца. Сгруппируйте месяцы в пары согласно старшим значащим 3-м битам адреса. Для каждой пары обозначение выхода Q («31 день») зависит от младшего значащего адресного бита А0. Сравните с рис. 8.41. Наконец, напрягитесь и проверьте, что схема делает на самом деле, если заданный месяц имеет 31 день.}

Забавное примечание: оказывается, что данную таблицу истинности можно реализовать только с одним вентилем «исключающее или», если использовать для несуществующих месяцев знак X (любое значение)! Попытайтесь сделать это самостоятельно. Это даст вам возможность приобрести опыт в составлении карт Карно.

Дешифраторы как обобщенные таблицы истинности. Дешифраторы также позволяют упростить комбинационную логику, особенно в тех случаях, когда нужно получить несколько одновременно действующих выходных сигналов. В качестве примера попробуем составить схему преобразования двоично-десятичного кода в код с избытком 3. Таблица истинности для такого преобразования имеет вид:

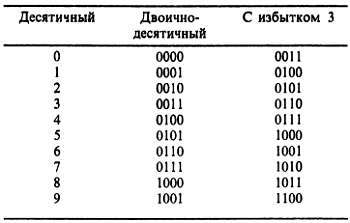
Мы здесь используем 4-разрядный (в двоично-десятичном коде) вход как адрес для дешифратора, а выходы дешифратора (в отрицательной логике) служат в качестве входов для нескольких вентилей ИЛИ, формирующих выходные биты, как показано на рис. 8.42.

Заметим, что в этой схеме выходные биты не являются взаимно исключающими. Аналогичную схему можно использовать в качестве устройства для задания рабочих циклов в стиральной машине: при каждом состоянии входа выполняются различные функции (подача воды, заполнение, вращение барабана и т. д.). Вскоре вы увидите, каким образом вырабатывается последовательность двоичных кодов, следующих через равные промежутки времени. Индивидуальные выходы дешифратора носят название «минтермы» и соответствуют позициям на карте Карно.

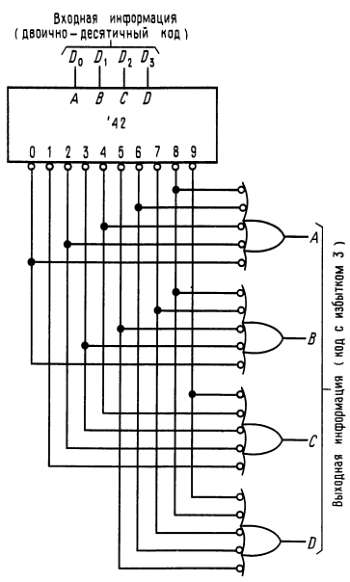
Рис. 8.42. Преобразование кодов на уровне минтермов: преобразование двоично-десятичного кода в код с избытком 3 (устаревший код, сохранившийся с 1-го издания книги).

ПЗУ и программируемая логика. Эти ИС позволяют вам программировать их внутренние связи. В этом смысле они фактически являются устройствами с памятью и будут рассматриваться позднее, вместе с триггерами, регистрами и т. п. Однако после программирования они являются строго комбинационными, хотя существуют также последовательностные программируемые логические устройства (см. разд. 8.27), они так полезны, что будут обсуждаться сейчас.

ПЗУ. ПЗУ (постоянное запоминающее устройство) содержит битовый образ (обычно 4 или 8 разрядов, параллельный выход) для каждого конкретного адреса, приложенного ко входу. Например, 1Кx8 ПЗУ выдает восемь выходных бит на каждое из 1024 входных состояний, определяемых 10-разрядным входным адресом (рис. 8.43).

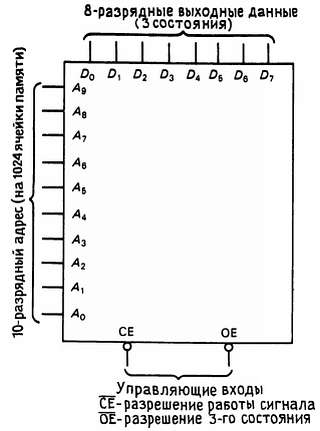
Рис. 8.43.

Любая комбинационная таблица истинности может быть запрограммирована в ПЗУ, обеспечивающем достаточное число входных линий (адреса). Например, ПЗУ 1Кx8 можно использовать для реализации умножителя 4x4; в этом случае ограничение на «ширину» (8 разрядов), не действует (так как имеется 10 разрядов).

ПЗУ (а также программируемые логические устройства) являются энергонезависимым устройством, т. е. хранимая информация остается даже тогда, когда питание пропадает. ПЗУ подразделяются на несколько типов, в зависимости от их метода программирования: а) «Масочно-программируемые ПЗУ» имеют свое битовое содержание, созданное во время изготовления. б) «Программируемые ПЗУ» (ППЗУ) программируются пользователем: ПЗУ имеют тонкие перемычки, которые могут пережигаться (подобно предохранителям) посредством подачи адреса и управляющих сигналов; они обладают высоким быстродействием (25–50 нс), относительно большим потреблением (биполярные 0,5–1 Вт), размерами от малых до средних (от 32x8 до 8Кx8). «Стираемые программируемые ПЗУ» (СППЗУ) хранят свои биты как заряды на плавающих МОП-вентилях; информация в них может стираться посредством облучения их интенсивным ультрафиолетовым светом в течение нескольких минут (они имеют прозрачное кварцевое стекло); выполняются по n-МОП и КМОП-технологии и значительно медленнее (200 нc) при низком потреблении (частично в режиме хранения), имеют достаточно большой размер (8Кx8 и 128Кx8). Современные КМОП СППЗУ достигают быстродействия биполярных ПЗУ (35 нс). Известен вариант — «однократно-программируемый» (ОКП), он содержит идентичный кристалл, но не имеет кварцевого окна для экономии и простоты, г) «Электрические стираемые программируемые ПЗУ» (ЭСППЗУ) подобны СППЗ, но могут программироваться и стираться электрически прямо в схеме с использованием стандартных напряжений питания (+5 В).

ПЗУ находят широкое использование в компьютерах и микропроцессорах, где они используются для сохранения законченных программ и таблиц данных; мы увидим их снова в гл. 11. Однако вы всегда должны помнить о небольших ПЗУ, как о замене сложных вентильных матриц.

Программируемая логика. ПМЛ (программируемая матричная логика; PAL-товарный знак фирмы Monolitic Memories Inc.) и ПЛМ (программируемые логические матрицы) являются двумя основными видами программируемой логики. Они являются ИС со многими вентилями, связи между которыми могут программироваться (подобно ПЗУ) для формирования желательных логических функций. Они выполняются как в биполярном, так и в КМОП-вариантах, первые используют прожигаемые перемычки (однократно-программируемые), вторые — плавающие вентильные КМОП схемы (ультрафиолетового или электрического стирания). Вы не можете запрограммировать любую связь, какую желаете — вы будете ограничены встроенной структурой. Рис. 8.44 показывает основные схемы комбинационных (не регистровых) ПЛМ и ПМЛ.

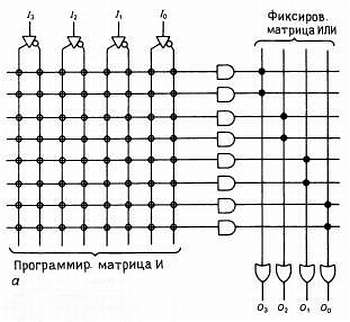
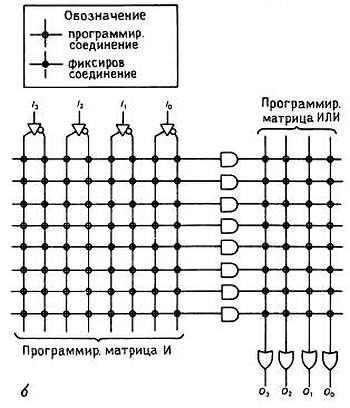
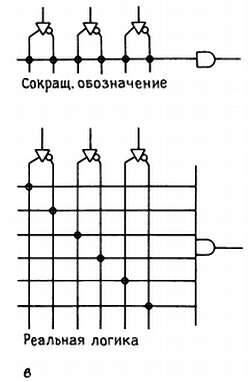
Рис. 8.44. Программируемая логика: а — ПЛМ; б — ПМЛ; в — фрагмент программируемых соединений с многовходовым вентилем И; кружками обозначены плавкие перемычки или другие программируемые соединения.

Для простоты на этом рисунке вентили И или ИЛИ нарисованы с одним входом, хотя в действительности они являются много-входовыми вентилями с входом для каждого перекрестия. Каждый выход (с 3 состояниями) комбинационной ПМЛ выводится от вентиля ИЛИ, а каждый вход подсоединяется к вентилю И с дюжинами входов. Например, 16L8 (рис. 8.45) имеет восемь 7-входовых вентилей ИЛИ; каждый возможный сигнал достижим для каждого вентиля И, включая 10 входных контактов (и инверторы для них) и 8-выходных контактов (и инверторы к ним).

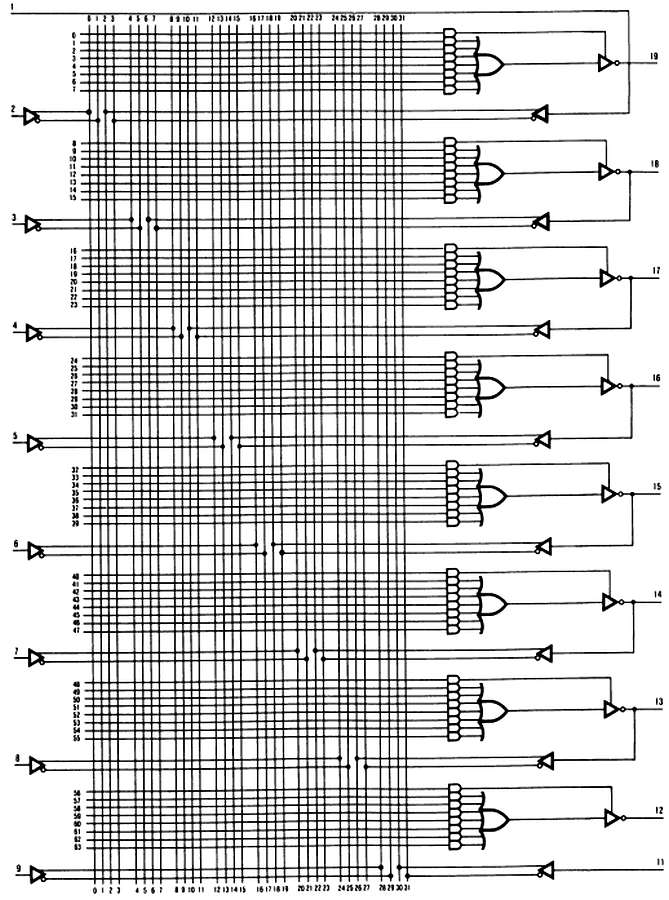
Рис. 8.45. Комбинационная ПМЛ 16L8 имеет 10 специальных входов, 2 специальных выхода и 6 двунаправленных линии входа/выхода (с 3-м состоянием). «16L8» означает 16 входов (макс), 8 выходов (макс.) (низкий уровень - истинное значение).

_{(с разрешения фирмы Advanced Micro Devices, Калифорния.)}

Разрешение третьего состояния также устанавливается от 32-входового вентиля И. ПЛМ подобна ПМЛ, но обладает большей гибкостью — выходы вентилей И могут связываться со входами вентилей ИЛИ в любой комбинации (т. е. программироваться), что предпочтительней, чем жесткое присоединение, как в ПМЛ.

Заметим, что ПМЛ и ПЛМ, которые мы описывали, являются комбинационными устройствами (т. е. выполнены только на вентилях, без памяти). Другой разновидностью программируемой логики является последовательностная логика, т. е. имеющая память (регистры), подробно мы рассмотрим их в, следующем разделе. Для использования ПМЛ и ПЛМ вы должны иметь программатор, как часть аппаратного обеспечения, который знает, как прожигать перемычки (или другие типы программируемых средств) и проверить окончательный результат. Все программаторы имеют связь через последовательный порт с микрокомпьютером (стандартное средство связи на IBM PC или совместимой с ней), на котором вы работаете с программным обеспечением программатора. Некоторые из современных программаторов включают одноплатный компьютер, который работает с собственным программным обеспечением.

Простейшее программное обеспечение просто позволяет вам выбрать перемычки для прожигания; вы изображаете это в зависимости от того, какую логику вы хотите получить на уровне вентилей, затем перечисляете (или помечаете на графическом дисплее) эти перемычки. Рис. 8.46 показывает простой пример для функции исключающее ИЛИ на два входа на одном из выходов ПМЛ.

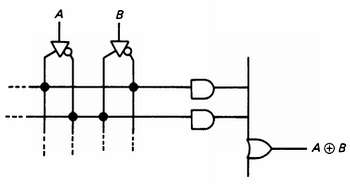
Рис. 8.46. Исключающее ИЛИ на ПМЛ.

Хорошие программаторы позволяют вам задавать буквы выражения (если они вам известны) или таблицы истинности; программное обеспечение затем делает остальное, включая минимизацию, моделирование и программирование. Хотя ПЛМ более гибкие, фаворитом в современном проектировании являются ПМЛ. Это из-за того, что они быстрее (так как сигнал проходит только через один массив перемычек), дешевле и обычно удовлетворяют задаче. Как мы увидим позже, новые ПМЛ, использующие «макроячейки» и «складную архитектуру» дают вам некоторую дополнительную гибкость в проектировании на ПМЛ с фиксированными ИЛИ-вентилями. Таким образом, ПМЛ представляют собой гибкую и компактную альтернативу ИС с фиксированными функциями и не должны выпадать из виду у серьезного проектировщика схем. Мы покажем, как (и где) применять программируемую логику с использованием полезных хитростей в разд. 8.27.