Приложение 3 LС-ФИЛЬТРЫ БАТТЕРВОРТА

Активные фильтры, как мы установили в гл. 5, очень удобно использовать на низких частотах, но на радиочастотах они неприменимы из-за условий, которые они предъявляют к ОУ в отношении скорости нарастания и ширины полосы пропускания. На частотах порядка 100 кГц и выше (а часто и на более низких частотах) лучше всего использовать фильтры, состоящие из индуктивностей и конденсаторов. Конечно, на СВЧ и микроволновых частотах вместо этих «ламповых» фильтров используют полосковые линии и резонаторы.

Для LC-фильтров, так же как и для активных фильтров, существуют различные методы анализа, различные характеристики. Например, можно использовать классические фильтры Баттерворта, Чебышева, Бесселя в качестве фильтров низких частот, высоких частот, полосовых и заграждающих фильтров.

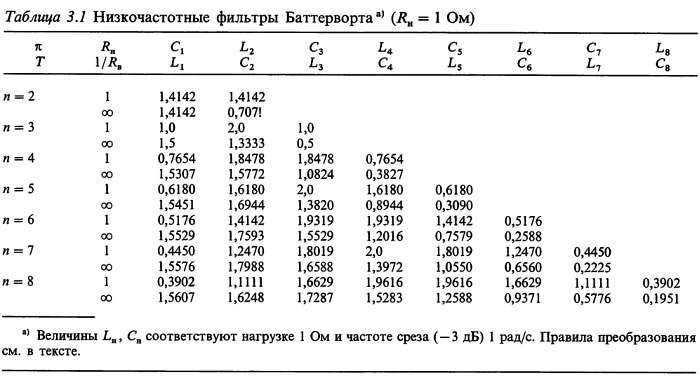
Оказывается, что проще всего разработать фильтр Баттерворта и на одной-двух страницах можно изложить всю информацию, необходимую для разработки НЧ- и ВЧ- LC-фильтров Баттерворта и даже привести примеры. Для получения более полной информации мы рекомендуем прекрасное руководство Зверева, указанное в библиографии. В табл. 3.1 приведены значения нормализованных индуктивностей и емкостей для фильтров НЧ различного порядка. С помощью этой таблицы определяют действительные значения емкостей и индуктивностей по формулам для соответствующих фильтров.

Формулы для фильтров НЧ:

L_п (действ.) = R_нL_п (табл.)/ω, С_п (действ.) = С_п (табл.)/ωR_н, где R_н - сопротивление нагрузки, ω — угловая частота.

В табл. 3.1 приведены нормализованные значения для 2-8-полюсных фильтров НЧ для двух наиболее общих случаев, а именно: (а) сопротивление источника и нагрузки равны; (б) одно из сопротивлений, источника или нагрузки, значительно больше другого.

Прежде чем прибегать к помощи таблицы, решите, используя характеристику Баттерворта (графики приведены в разд. 5.05 и 5.07), сколько полюсов вам нужно иметь. Затем, используя приведенные выше уравнения, определите конфигурацию фильтра (И- или П-образная, см. рис. 3.1) и величины компонентов. Для одинаковых сопротивлений источника и нагрузки подходит любая конфигурация: П-образные фильтры предпочтительнее, так как для них требуется меньшее количество индуктивностей. Если сопротивление нагрузки значительно выше (ниже), чем сопротивление источника, то следует использовать Т-образный (П-образные) фильтр.

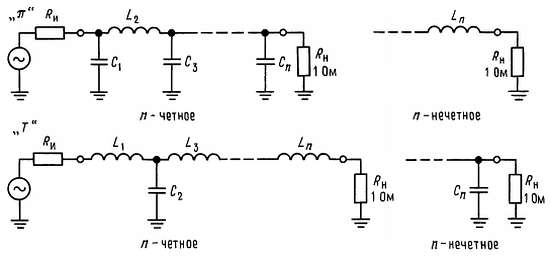
Рис. 3.1.

При разработке фильтра высоких частот воспользуйтесь описанной процедурой для того, чтобы выбрать конфигурацию фильтра и определить необходимое число полюсов. Затем проделайте универсальное преобразование фильтра НЧ в фильтр ВЧ, показанное на рис. 3.2. Оно заключается в простой замене индуктивностей конденсаторами и наоборот.

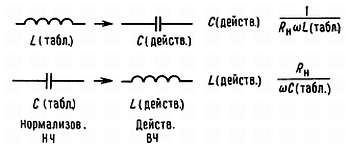
Рис. 3.2.

Действительные величины компонентов определяются по табл. 3.1 с помощью формул:

Формулы для ВЧ:

L_п (действ.) = R_н/ωC_н (табл.), С_п (действ.) = 1/R_нωL_п (табл.).

Приведенные ниже примеры показывают, как использовать табличные значения при разработке фильтров НЧ и ВЧ.

Пример I. Требуется разработать 5-полюсный фильтр НЧ при условии, что сопротивления нагрузки и источника равны 75 Ом, а частота среза (—3 дБ) составляет 1 МГц.

Для уменьшения числа индуктивностей выберем П-образный фильтр. С помощью формул преобразования получим:

С₁ = С₅ = 0,618/2π·10⁶·75 = 1310 пФ,

L₂ = L₄ = 75·1,618/2π·10⁶ = 19,3 мкГ,

С₃ = 2/2π·10⁶·75 = 4240 пФ.

Полная схема фильтра показана на рис. 3.3.

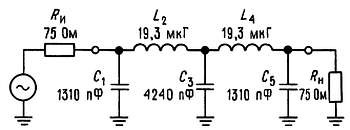
Рис. 3.3.

Отметим, что все фильтры с одинаковыми сопротивлениями источника и нагрузки имеют симметричную конфигурацию.

Пример II. Требуется разработать 3-полюсный фильтр НЧ при условии, что импеданс источника равен 50 Ом, сопротивление нагрузки равно 10 кОм, а частота среза составляет 100 кГц.

В связи с тем что R_и << R_н, выберем T-образную конфигурацию. Воспользуемся формулами преобразования, учитывая, что R_н = 10 кОм:

L₁ = 10⁴·1,5/2π·10⁵ = 23,9 мГ,

С₂ = 1,3333/2π·10⁵·10₄ = 212 пФ,

L₃ = 10⁴·0,5/2π·10⁵ = 7,96 мГ.

Полная схема фильтра показана на рис. 3.4.

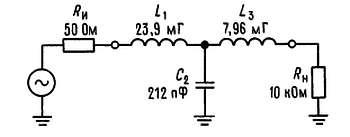
Рис. 3.4.

Пример III. Требуется разработать 4-полюсный фильтр НЧ при условии, что сопротивление источника (напряжения) равно нулю, сопротивление нагрузки равно 75 Ом, а частота среза составляет 10 МГц.

Как и в предыдущем примере, выберем T-образную конфигурацию, так как R_и << R. Воспользуемся формулами преобразования:

L₁ = 75·1,5307/2π·10⁷ = 1,83 мкГ,

С₂ = 1,5772/2π·10⁷·75 = 335 пФ,

L₁ = 75·1,0824/2π·10⁷ = 1,29 мкГ,

С₄ = 0,3827/2π·10⁷·75 = 81,2 пФ.

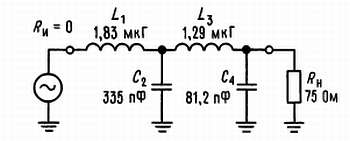
Рис. 3.5.

Пример IV. Требуется разработать 2-полюсный фильтр НЧ при условии, что в качестве источника используется источник тока, сопротивление нагрузки равно 1 кОм, а частота среза составляет 10 кГц.

Выберем П-образную конфигурацию, так как R_и << R. Воспользуемся формулами преобразования:

C₁ = 1,4142/2π·10⁴·10³ = 0,0225 мкФ,

L₂ = 10³·0,7071/2π·10⁴ = 11,3 мГ.

Полная схема фильтра показана на рис. 3.6.

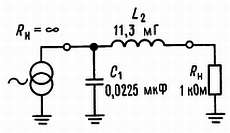
Рис. 3.6.

Пример V. Требуется разработать 3-полюсный фильтр ВЧ при условии, что сопротивление источника и нагрузки равно 52 Ом, а частота среза составляет 6 МГц.

Возьмем ^образный фильтр и заменим индуктивности на конденсаторы и наоборот:

С₁ = С3 = 1/52·2π·6·10⁶·1,0 = 510 пФ,

L₂ = 52/2π·6·10⁶·2,0 = 0,690 мкГ.

Полная схема фильтра показана на рис. 3.7.

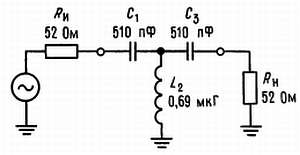
Рис. 3.7.

Хотелось бы подчеркнуть, что разработка пассивных фильтров представляет собой обширный предмет, включающий в себя множество разнообразных вопросов, и он, конечно, не исчерпывается простой таблицей фильтров Баттерворта.