5. Harmonice Mundi

Работа была завершена в 1618 году, через три месяца после смерти дочери Катарины и через три дня после дефенестраций в Праге. Никакой иронии в названии не предполагалось. Иронию Кеплер позволил себе в ссылке (к шестой главе пятой книги), где обсуждаются звуки, издаваемые различными планетами во время их движения по своим орбитам: "Земля поет Ми-Фа-Ми, из чего мы можем сделать заключение, что в наших краях царят Невзгоды (Miseris) и Голод (Fame)".

Мировая Гармония – это "Песнь Песней" математика, направленная "главному оркестратору творения"; это мечтания Иова об идеальной вселенной. Если читать эту книгу попеременно с письмами Кеплера относительно обвинения в ведьмовстве, относительно его отлучения от церкви, относительно войны и смерти его ребенка, может появиться впечатление, будто переключаешься между различными пьесами стратфордского современника. Письма кажутся эхом монолога короля Лира:

Дуй, ветер! Дуй, пока не лопнут щеки!

Лей, дождь, как из ведра и затопи

Верхушки флюгеров и колоколен!

Вы, стрелы молний, быстрые, как мысль,

Деревья расщепляющие, жгите

Мою седую голову! Ты, гром,

В лепешку сплюсни выпуклость вселенной

И в прах развей прообразы вещей

И семена людей неблагодарных! (перевод Б. Пастернака)

Но вот эпиграфом книги могло бы быть:

Как сладко дремлет лунный свет на горке!

Дай сядем здесь, - пусть музыки звучанье

Нам слух ласкает; тишине и ночи

Подходит звук гармонии сладчайший.

Сядь, Джессика. Взгляни, как небосвод

Весь выложен кружками золотыми;

И самый малый, если посмотреть,

Поет в своем движенье, точно ангел,

И вторит юнооким херувимам.

Гармония подобная живет

В бессмертных душах; но пока она

Земною, грязной оболочкой праха

Прикрыта грубо, мы ее не слышим.

(В. Шекспир Венецианский купец, перевод Т. Щепкиной-Куперник, Акт V, сцена 1)

Мировая Гармония – это продолжение Космической Тайны и вершина жизненного наваждения Кеплера. Если упрощать, то Кеплер пытается здесь раскрыть главнейшую тайну Вселенной посредством всеохватного синтеза геометрии, музыки, астрологии, астрономии и эпистемологии[282]. Это была первая попытка такого рода со времен Платона и последняя до наших дней. После Кеплера вновь началось дробление опытного знания, наука отделилась от религии, религия – от искусства, наполнение – от формы, материя – от сознания.

Вся работа разделена на пять книг. Первые две разбираются с концепцией гармонии в математике; последующие три – с приложением данной концепции к музыке, астрологии и астрономии, именно в таком порядке.

Что конкретно Кеплер понимал под "гармонией"? Некие геометрические пропорции, которые, как он открыл, отражаются повсюду, архетипы универсального порядка, из которых выводятся законы движения планет, гармонии в музыке, изменчивость погоды и судьбы людей. Эти геометрические соотношения являются чистыми гармониями, которые направляют Господа в трудах Творения; сенсорная гармония, которую мы ощущаем, слушая музыкальные созвучия, это всего лишь эхо их. Но тот врожденный инстинкт человека, который заставляет его душу резонировать с музыкой, дает ему ключ к разгадке природы математических гармоний, лежащих в самой ее основе. Пифагорейцы открыли, что октава появляется при соотношении 1:2 между длинами двух вибрирующих струн; квинта – при соотношении 2:3; кварта – при соотношении 3:4 и так далее. Но они ошибались, говорит Кеплер, когда искали объяснения этого чудесного факта в оккультной нумерологии. Объяснение того, почему соотношение 3:5, к примеру, дает аккорд, но 3:7 – диссонанс, необходимо искать не в арифметических, но геометрических рассуждениях. Давайте представим себе струну, чьи колебания производят звук, свернутую в окружность, чьи концы соединены. Теперь эта окружность может удовлетворительно делиться на части путем вписывания в нее симметрических многоугольников с различным количеством сторон. Например, вписанный пятиугольник разделит окружность на части, которые соотносятся к длине всей окружности как 1/5 и 4/5 соответственно – обе части дают консонансные созвучия.

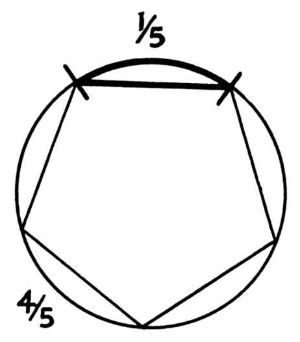
Но семиугольник даст соотношения 1/7 и 6/7 – и то, и другое, диссонансы. Почему? По мнению Кеплера, ответ заключается в следующем: потому что пятиугольник можно построить с помощью циркуля и линейки, а вот семиугольник – нет. Циркуль с линейкой – это единственные разрешенные в классической геометрии инструменты. Но геометрия – это единственный язык, который помогает человеку понять работу божественного ума. Следовательно, те фигуры, которые нельзя построить посредством циркуля и линейки – такие как семиугольник, полигоны с 11, 13 или 17 сторонами – являются каким-то образом нечистыми, поскольку они противостоят интеллекту. Они incibilis – непостижимые, inefabilis, непередаваемые словами, non-entia, не сущностные. "Именно в этом заключается причина, - поясняет Кеплер, - почему Господь не использовал семиугольники и другие фигуры такого рода, чтобы украсить мир".

Таким образом, чистые первичные гармонии, а так же их отражения – музыкальные созвучия, производятся путем деления окружности с помощью способных к построению, правильных многоугольников; а вот "непередаваемые словами" многоугольники порождают негармоничные звуки, так что они не используются в схеме Вселенной. К навязчивой идее пяти совершенных тел теперь прибавилась подобного рода навязчивая идея совершенных многоугольников. Первые – это трехмерные тела, вписанные в сферу; последние – двухмерные формы, вписанные в окружность. Между ними двоими имеется интимная, мистическая связь: сфера, необходимо помнить, для Кеплера является символом Святой Троицы; двухмерная плоскость символизирует материальный мир; пересечение сферы и плоскости – круг – принадлежит двум основополагающим понятиям и символизирует двойную природу человека: тело и душу.

И вновь факты не укладываются в схему, и это следовало объяснять путем изобретательных рассуждений. К примеру, 15-сторонний полигон можно построить циркулем и линейкой, но он не порождает музыкальных консонансов. Более того, число полигонов, которых можно построить "по правилам" является бесконечным, но Кеплеру было нужно всего семь гармонических соотношений для своей шкалы (октава, большая и малая секста, квинта, кварта, большая и малая терция). Еще, гармонии следовало аранжировать по иерархии меняющихся степеней "познания" или совершенства. Кеплер посвятил этому фантастическому предприятию столько же усилий и трудов, как и определению орбиты Марса. Под конец, к собственному удовлетворению, он вывел все свои семь гармоний, путем применения некоторых весьма сложных правил, из правильных многоугольников. То есть, он проследил законы музыки назад, до замысла Верховного Геометра.

В последующих разделах Кеплер применяет свои гармонические соотношения ко всем предметам, которые только существуют под Солнцем: к метафизике и эпистемологии, к политике, психологии и физиогномике; к архитектуре и поэзии, к метеорологии и астрологии. И потом, в пятой – и последней – книге, он возвращается к космологии, чтобы завершить свое головокружительное строение. Вселенная, которую он выстроил в юности вокруг пяти совершенных тел, не совсем соответствовала наблюдаемым фактам. Теперь же он привлек двухмерную призрачную армию многоугольников на спасение своим осажденным телам. Гармонические соотношения каким-то образом должны были втиснуться между этими телами, чтобы заполнить щели и сгладить все несоответствия.

Но вот как следовало это сделать? Как гармонии могли быть прилажены в схему Вселенной, заполненную эллиптическими орбитами и неравномерными движениями, из которой, как могло показаться, вся симметрия и гармония были изгнаны? Как обычно, Кеплер доверяет читателю, и ради него "по косточкам" разбирает весь тот процесс, который привел его самого к решению. Поначалу он пытался приписать гармонические соотношения периодам вращения различных планет. После чего озадаченно написал: "Мы пришли к выводу, что Господь Творец не пожелал ввести гармонических пропорций в длительности планетарных годов" (Harmonice Mundi, книга V, глава 4).

Потом он предположил, что, может, величины объемов различных планет образуют гармонические последовательности. Но они не образовывали. После этого он попытался вставить самые большие и самые малые расстояния от солнца для каждой планеты в гармоническую шкалу. И снова нехорошо. Затем пришла очередь вариаций времени, необходимого планете для покрытия единицы длины ее орбиты. И снова не так. В конце концов, Кеплеру пришла в голову идея перенести место наблюдателя в центр Вселенной и проверить изменения угловой скорости, независимо от расстояния, как это видно с Солнца. И вот тут: бинго! Сработало!

Результаты были даже более приятными, чем автор ожидал. Сатурн, к примеру, находясь дальше всего от Солнца, в афелии, движется со скоростью 106 секунд дуги в день; когда же он находится ближе всего к Солнцу, его скорость максимальна и составляет 135 секунд дуги за сутки. Соотношение между двумя экстремальными скоростями составляет 106 к 135, а это всего на две несчастные секунды отличается от 4:5 – большой терции. С такими же, очень малыми отклонениями (которые замечательно объясняются в конце), отношение самой медленной и самой большой скорости Юпитера представляет собой малую терцию; у Марса – квинту и так далее. И для каждой планеты рассматривается само по себе. Но когда Кеплер сравнил крайние угловые скорости пар различных планет, результаты получились еще более волшебными:

С первого взгляда Солнце Гармонии во всем своем блеске пробилось сквозь тучи!

Крайние (экстремальные) значения и действительно представляли собой интервалы полной музыкальной шкалы. Но это еще не все: если мы начнем с самой дальней планеты, Сатурна в афелии, гамма будет в мажоре; если же мы начнем с Сатурна в перигелии – она будет в миноре. Наконец, если несколько планет одновременно находятся в экстремальных точках своих соответственных орбит, результатом становится мотет[283], где Сатурн с Юпитером представляют собой басы, Марс – тенор, Земля и Венера – контральто, а Меркурий – сопрано. И при некоторых случаях всех шестерых можно слышать вместе:

Небесные движения являются ничем иным как непрерывной песнью для нескольких голосов (воспринимаемой разумом, но не ухом); музыкой, которая посредством противоречивых напряжений, посредством синкоп и каденций (которые люди используют в подражание природным разногласиям), прогрессирует в направлении заранее определенных, квази-шестиголосых клаузур (первичных пространственных идей всего художественного произведения – Академ.Словарь), устанавливая тем самым ориентиры в неизмеримом потоке времени. И уже не удивительно, что человек, в подражание собственному создателю, наконец-то раскрыл искусство гармонической песни, которая была неизвестна древним. Человек желал воспроизвести непрерывность космического времени за его краткий отрезок, посредством искусной симфонии на несколько голосов, чтобы получить опытный образчик радости Божественного Творца его Собственными Творениями, и принять участие в его радости, творя музыку в подражание Господу (Harmonice Mundi, книга V, глава 7).

Храм был завершен. Кеплер закончил свою книгу 27 мая 1618 года, когда шла одна из самых судьбоносных недель европейской истории[284]:

Понапрасну Бог Войны ревет, рычит, гремит и пытается вмешаться со всеми своими бомбардами, трубами и всем своим тарарамом (…) Давайте презирать все те варварские похоти, что перекатываются эхом через эти благородные земли, пробуждая лишь наше понимание и стремление к гармонии (из Посвящения лорду Напьеру Эфемерид на 1620 год).

Из мрачных бездн он воспаряет к высотам орфического экстаза:

Идея, осенившая меня двадцать пять лет назад, еще до того, как я открыл пять совершенных тел, вписанных между небесными орбитами (…); которую шестнадцать лет назад я провозгласил в качестве окончательной цели всех исследований; которая заставила меня посвятить лучшие годы моей жизни изучению астрономии, присоединиться к Тихо Браге и выбрать Прагу в качестве места жительства – вот что я имею, с помощью Господа, который подложил под мой энтузиазм огонь и поддерживал во мне неуемное желание; который держал в готовности мою жизнь и разум, и который также обеспечил мне все необходимое благодаря щедрости двух императоров и Штатов моей земли, Верхней Австрии – и вот теперь, после того, как я исполнил свои астрономические обязанности ad satietatum (досыта - лат.), наконец-то я познал свет (…) Ощутив первые проблески зари восемнадцать месяцев назад, а дневной свет – три месяца назад, но наиболее замечательное видение божественного Солнца – всего несколько дней назад; теперь уже ничто не сможет заставить меня отвернуть. Да, я предаюсь священному неистовству. Со смехом бросаю я вызов всем смертным этим открытым признанием: я похитил золотые сосуды египтян[285], чтобы из них изготовить дарохранительницу для своего Бога, далеко от границ Египта. Если вы простите меня, я буду рад. Если вы будете злиться, я это вынесу. Глядите, я обязан бросить жребий, и я пишу книгу для своих современников – или же для потомков. Для меня это одно и то же. Для читателя это может продлиться и сотню лет, но ведь Господу тоже пришлось ждать шесть тысяч лет свидетельства (…) (Введение к книге V Harmonice Mundi).