5. Последний синтез

Первым шагом Ньютона было свершение в воображении того, чего не добилась история: он устроил встречу Кеплера с Галилеем. А точнее, он объединил половину Кеплера с половиной Галилея, а все лишнее отбросил.

Местом встречи была Луна. Джеремия Хоррокс – английский юный гений, скончавшийся в возрасте двадцати одного года – применил законы Кеплера к лунной орбите. Это дало Ньютону половину синтеза. Вторую половинку он обнаружил в разработанных Галилеем законах движения снарядов в непосредственной близости Земли. Ньютон отождествил кеплеровскую орбиту Луны с галилеевской траекторией снаряда, который постоянно спадал к Земле, но не мог достичь ее по причине быстрого движения по касательной. В трактате Система Мира (System of the World) процесс размышлений Ньютона представлен следующим образом:

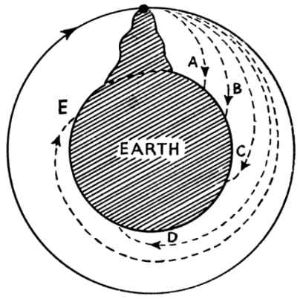
Если снаряд выстрелить с вершины горы, тогда прямолинейная траектория его полета будет скривлено земным притяжением. В зависимости от приданной ему начальной скорости, снаряд станет перемещаться по кривым А, В, С , D или Е. Если начальная скорость превысит некое критическое значение, тогда снаряд очертит круг и ли эллипс, "и возвратится к той горе, с которой его выстрелили". Более того, согласно второму закону Кеплера, "его скорость после возврата будет не меньшей, чем вначале, а при сохранении той же скорости он будет все время вычерчивать ту же самую кривую, в соответствии с тем же законом (…) и кружить по небу точно так же, как планеты по своим орбитам". Иными словами, в своем умственном эксперименте Ньютон создал искусственный спутник, почти что за три сотни лет до того, как техника была способна реализовать эту идею.

Основной концепцией, на которой опирается небесная механика у Ньютона, является совместное воздействие двух сил: силы гравитации, которая притягивает планету к Солнцу, и центробежной силы, которая эту первую силу уравновешивает. Чаще всего применяемой иллюстрацией к данной концепции является вращение камнем, привязанным на конце веревочки. Сила, которая натягивает веревку, это центробежная сила камня; прочность веревки, вызывающая то, что камень остается на орбите, соответствует гравитационному притяжению.

Но почему же планета описывает эллиптическую траекторию, а не окружность? Если говорить в упрощении, то потому, что когда я вращаю камнем в воздухе, веревка обладает определенной длиной, и она не растягивается, а вот притяжение Солнца с изменением расстояния тоже изменится. В результате этого, камень вращается по идеальной окружности, а вот планета поступала бы так лишь в том случае, если бы ее скорость по касательной и следующая отсюда центробежная сила уравнивались бы с притяжением Солнца. Если скорость больше или меньше, чем требуемая, тогда планета движется не по окружности, а по эллипсу. Если бы скорость была слишком малой, орбита планеты пересеклась бы с поверхностью Солнца, что вызвало бы ее падение на Солнце, точно так же, как метеоры, заторможенные трением атмосферы, падают на Землю. В свою очередь, чем больше скорость по касательной по сравнению с силой притяжения, тем большим станет "вытягивание" эллипса, пока, в конце концов, один конец, если можно так сказать, растянется до бесконечности, и эллипс превратится в параболу: такую траекторию имеют кометы, прилетающие к нам из далекого космического пространства, отклоняются от своего курса под влиянием Солнца, но не настолько, чтобы дать ему себя "сцапать", после чего они вновь исчезают в пространстве.

Почему планеты должны были двигаться по эллиптическим орбитам, легко доказать математически. Но весь этот механизм можно представить и как перетягивание каната между притяжением и центробежной силой. Если бы веревка, на конце которой вращается камень, могла растягиваться, она попеременно удлинялась бы и сокращалась, из-за чего камень двигался бы по овалу[348]. Другим способом представить себе этот процесс является следующий: когда планета приближается к Солнцу, ее скорость возрастает. Она мчится прямиком, но удерживающая ее ладонь гравитации оборачивает планету вокруг Солнца, в результате чего та мчится в противоположном направлении. Если бы скорость планеты при подходе к Солнцу составляла ровно столько, чтобы предотвратить падение на Солнце, та вращалась бы по окружности. Но, поскольку скорость была чуточку большей, на противоположной стороне траектория "выгнется" наружу, что, в свою очередь, приведет к падению скорости и искривлению траектории уже "вовнутрь" под воздействием солнечного притяжения. После прохождения через афелий планета опять приближается к Солнцу, и весь цикл повторяется.

Эксцентричность орбиты представляет собой меру ее отклонения от окружности. Эксцентриситеты планет невелики, поскольку, учитывая общее происхождение всех тел Солнечной Системы, их скорости по касательной практически уравновешиваются с воздействием притяжения.

Но во времена Ньютона все это опиралось только лишь на домыслах, а эпоха чисто спекулятивных гипотез уже минула. И таким совершенно сумасшедшим домыслом была гипотеза, будто бы Луна постоянно "падает" на Землю, словно пушечное ядро или словно знаменитое яблоко в Саду в Вулторпе – другими словами, что земное притяжение достигает Луны, солнечное притяжение – до самых планет, а межзвездное пространство "заполнено" или "заряжено" гравитацией. Чтобы преобразовать этот странный домысел в научную теорию, Ньютон должен был представить точное математическое доказательство.

Это означало, что ему следовало вычислить центробежную силу Луны[349] и силу притяжения, с которой, якобы, Земля воздействует на Луну, а так же показать, что взаимное воздействие этих сил в результате дает теоретическую орбиту, которая совпадает с наблюдаемой орбитой Луны.

Чтобы осуществить данную операцию, Ньютону, во-первых, необходимо было знать функцию, в соответствии с которой земное притяжение уменьшается вместе с расстоянием. Яблоко падало с дерева с известным прибавлением скорости десяти ярдов в секунду в каждую секунду. А с каким ускорением двигалась бы к Земле отдаленная Луна? Другими словами, Ньютону нужно было открыть закон притяжения, который говорит, что сила гравитации уменьшается в соответствии с квадратом расстояния. Во-вторых, ему нужно было знать точную удаленность Луны от Земли. В-третьих, ему следовало решить, можно ли трактовать два громадных шара Земли и Луны абстрактно, как будто бы вся их масса была собрана в одной центральной точке. И, наконец, для облегчения расчетов, орбиту Луны следовало рассматривать как окружность.

В результате всех этих сложностей первые вычисления Ньютона совпадали с фактами только лишь "довольно неплохо", а этого явно было недостаточно. И Ньютон почти что на два десятка лет эту проблему забросил.

А за эти два десятка лет экспедиция Жана Пикара в Кайенну предоставила более точные данные относительно диаметра Земли и ее отдаленности от Луны, сам Ньютон разработал свою разновидность счисления бесконечно малых, математический аппарат, без которого к этой проблеме нечего было и подходить, и, наконец, триумвират Галлей – Гук – Врен постоянно подгоняли последующие элементы головоломки. Оркестр дошел до той стадии, котгда уже можно было услышать отдельные группы инструментов, играющие определенные фрагменты. Нужен был лишь стук дирижерской палочки, чтобы все слилось в гармоничное звучание.

В 1686 году Ньютон, подгоняемый Галлеем, осуществил окончательный синтез. Он рассчитал силу, с которой Земля притягивает Луну, и показал, что в соединении с центробежной силой Луны, она создает наблюдаемую нами орбиту вечного спутника. Затем он вычислил силу, с которой Солнце притягивает отдельные планеты, и показал, что орбита, являющаяся результатом действия силы притяжения, которая уменьшается в соответствии с квадратом расстояния, представляет собой эллипс из первого закона Кеплера с Солнцем, находящимся в одном из фокусов. Он же показал и вещь совершенно противоположную: что эллиптичность орбиты требует, чтобы гравитационная сила изменялась именно таким образом. Краеугольным камнем системы стал третий закон Кеплера, соотносящий периоды обращения планет с их средними отдаленностями от Солнца, а второй закон – радиус-вектор покрывает одинаковые площади в одинаковые периоды времени – оказался верным для любой замкнутой орбиты. Потом Ньютон доказал, что кометы движутся либо по удлиненным эллипсам, либо по параболам, сбегая в пространство; что всякое тело над поверхностью Земли ведет себя так, как будто бы вся масса Земли была сконцентрирована в ее центре, благодаря чему, все небесные тела можно считать математическими точками. И наконец, все наблюдаемые движения во Вселенной он свел к четырем базовым законам: к закону инерции, к закону ускорения под действием силы, к закону действия и противодействия и к закону притяжения.

И чудо свершилось. Все обломки слетелись в одно целое в этом обращенном во времени взрыве и слились в одно гладкое, бесшовное, невинно выглядящее тело. Если бы Донн еще жил, свой плач он мог бы переписать в триумфальный возглас: "И все-то здесь в одном кусочке, и нет теперь неразберихи".

Движения Солнца, Луны и пяти бродячих звезд представляли собой главную космологическую проблему со времен древних вавилонян. Теперь, когда было доказано, что все эти движения подчиняются одним и тем же, простым законам, Солнечная Система была реорганизована в интегральное целое. Быстрый прогресс астрономии и астрофизики позволил ученым понять, что это целое, по сути своей, является частью еще большего целого: нашей Галактики, состоящей из миллионов очень похожих на Солнце звезд, некоторые из них тоже были окружены планетами, а еще, что наша Галактика выступает как одна из множества других галактик и туманностей на разных стадиях эволюции, но всеми ими управляет один и тот же универсальный набор законов.

Только эти дальнейшие открытия здесь нас уже не занимают. С момента публикации Принципов Ньютона в 1687 году космология сделалась наукой дисциплинированной, и на этом нам следует заканчивать рассказ о изменяющихся взглядах человека на вселенную. Дикий танец теней, отбрасываемых звездами на стену пещеры Платона преобразовался в упорядоченный и приличный викторианский вальс. Казалось, будто бы из мироздания исчезли все тайны, а божество было низведено к роли конституционного монарха, которого не свергают, желая поддержать традицию, но точно так же оно могло бы и не существовать, не имея какого-либо влияния на ход событий.

Нам же остается лишь обсудить кое-какие последствия всей этой истории.

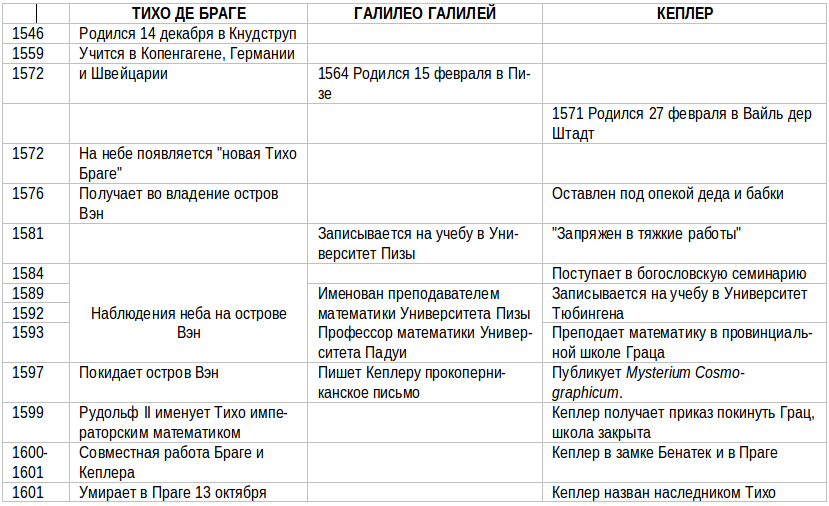
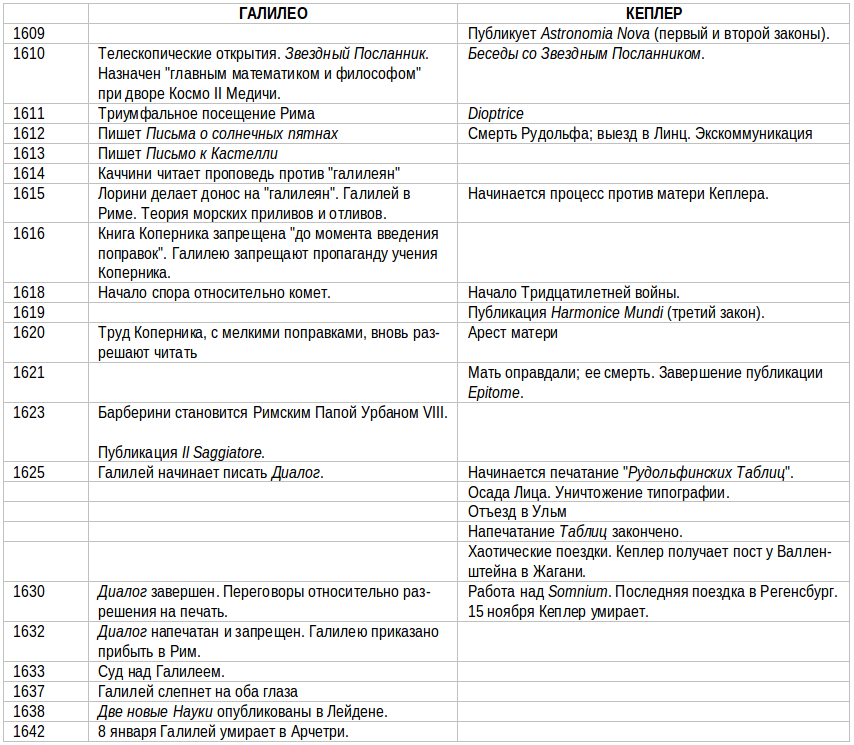
Хронологическая таблица к четвертой и пятой частям