1. Совершенные тела

Из фрустраций своего первого года пребывания в Граце Кеплер сбежал в космологические спекуляции, которыми весело занимался в дни своего обучения в Тюбингене. Только теперь спекуляции начали становиться и более интенсивными, и более математическими по своему характеру. Через год после приезда – а говоря точнее, 9 июля 1595 года, поскольку Кеплер тщательно задокументировал дату – он рисовал мелом фигуру на классной доске, как вдруг его голову посетила идея, да с такой силой, что он почувствовал, что в его руках очутился ключ к тайне творения. "Радость от моего открытия", - писал ученый впоследствии, - я никогда не был способен передать словами". Это открытие определило направление всей его жизни и осталось головным вдохновением.

Идея заключалась в том, что вселенная выстроена вокруг определенных симметричных фигур – треугольника, квадрата, пятиугольника и т.д. – которые образуют ее невидимый скелет. Перед тем, как перейти к деталям, будет лучше объяснить сразу, что сама идея была абсолютно неверной; тем не менее, именно она, возможно, привела к созданию Законов Кеплера, к разрушению античной Вселенной со всеми ее колесиками и к рождению современной космологии. Псевдо-открытие, которое и начало все это, описано в первой книге Кеплера, Misterium Cosmographicum[202], которую автор опубликовал в свои двадцать пять лет.

В Предисловии к работе Кеплер объясняет, как он пришел к своему "открытию". Еще будучи студентом в Тюбингене, он слышал от своего преподавателя астрономии, Маэстлина, о Копернике, и он соглашался с тем, что Солнце должно находиться в центре Вселенной "по физическим, или, если того хотите, по метафизическим причинам". После того он начал размышлять, почему существует всего шесть планет "а не двадцать или сто", и почему расстояния и скорости движения планет были такими, какими они есть. Так начался его поход к поиску законов планетарного движения.

Поначалу он попробовал рассудить, а может ли какая-нибудь из орбит по случайности сделаться в два, три или четыре раза больше другой. "Я напрасно потратил массу времени на эту задачу, на эту игру с числами, но никак не мог найти порядка ни в числовых пропорциях, ни в отклонениях от этих пропорций". Кеплер предупреждает читателя, что рассказ о его бесплодных попытках способен чрезвычайно укачать его, словно волны на море". Поскольку эго рассуждения ни к чему не привели, он попробовал "удивительно смелое решение": Кеплер вставил дополнительную планету между Меркурием и Венерой, затем еще одну, между Юпитером и Марсом, обе сознательно очень малые, чтобы их можно было видеть, надеясь на то, что теперь-то обнаружит какую-то осмысленную последовательность соотношений. Но и этот подход не сработал, как не срабатывали другие подходы, которые он последовательно испытывал.

Я потратил практически все лето на эту тяжкую работу. В конце концов, я пришел к истинным фактам по совершенно мелкому поводу. Надеюсь, что это Божественное Провидение устроило все так, что то, чего не мог я достичь, применяя все усилия, было дано мне по чистой случайности; все сильнее мне кажется, что так случилось потому, что я всегда молил Господа, чтобы он смог завершить мой пан успехом, если все сказанное Коперником было правдой.

Причиной того приведшего к столь решительным действиям события была упомянутая выше лекция в классе, в ходе которой Кеплер должен был вычертить, по совершенно иным причинам, геометрическую фигуру на классной доске. Сама фигура изображала (тут я должен описать ее упрощенно) треугольник, вписанный между двумя окружностями; другими словами, внешняя окружность была описана вокруг треугольника, а внутренняя окружность – вписана в него.

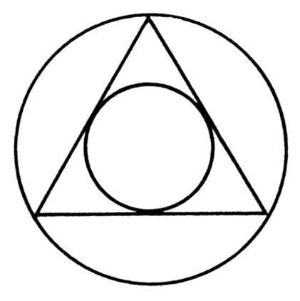
Когда Кеплер глядел на эти две окружности, совершенно неожиданно ему пришло в голову, что их отношение соответствовало отношению орбит Сатурна и Юпитера. Остальная часть идеи пришла будто вспышка. Сатурн и Юпитер являются "первыми" (то есть, двумя самыми внешними) планетами, а "треугольник – это первая фигура в геометрии. Тут же я попытался вписать в следующий интервал, между Юпитером и Марсом, квадрат; между Марсом и Землей – пятиугольник, между Землей и Венерой – шестиугольник…"

Это не сработало – пока что еще нет, но Кеплер чувствовал, что близко подобрался к тайне. "А теперь я пошел дальше. Зачем выискивать двухмерные формы, чтобы подогнать орбиты в пространстве? Необходимо искать трехмерные фигуры – и вот, дорогой мой читатель, гляди, открытие находится в твоих руках!..."

Вся штука вот в чем. На двухмерной плоскости можно создать любое количество правильных многоугольников; но вот в трехмерном пространстве можно сконструировать ограниченное число правильных тел. Этими "совершенными телами", в которых все грани идентичны являются: (1) тетраэдр (пирамида), ограниченный четырьмя равносторонними треугольниками; (2) куб; (3) октаэдр (восемь равносторонних треугольников); (4) додекаэдр (двенадцать пятиугольников) и (5) икосаэдр (двадцать равносторонних треугольников).

Еще они назывались "пифагоровыми" или "платоновыми" телами. Поскольку каждое из них было абсолютно симметричным, его можно было вписать в сферу, так что все вершины такого тела (углы) лежали на поверхности сферы. И точно так же, каждое из этих тел можно было описать вокруг сферы, чтобы сфера касалась каждой грани в ее центре. Удивительный факт, присущий природе трехмерного пространства, что (как доказал Эвклид) число правильных тел ограничено этими пятью видами. Какую бы форму не избрали в качестве грани, никакого другого абсолютно совершенного тела невозможно сконструировать – если не считать этих пяти. Любые иные комбинации просто невозможно подогнать в единое целое.

Итак, существует всего только пять совершенных тел – и пять интервалов между планетами! Невозможно было поверить, что такое соотношение возникло случайно, а не по божественному плану. Это же давало полный ответ на вопрос, почему существует только шесть планет, а "не двадцать или сто". Здесь же был ответ на вопрос, почему расстояния между планетами были такими, какими они были. Планеты должны были размещаться таким образом, чтобы пять тел могли быть точно подогнаны в эти интервалы, словно невидимый скелет или рама. И вот!, они вмещались в эти интервалы! Во всяком случае, казалось, что они, более или менее, вмещаются. В орбиту (или сферу) Сатурна Кеплер вписал куб; после чего вписал в куб другую сферу – сферу или орбиту Юпитера. В эту сферу был вписан тетраэдр, после чего в него была вписана орбита Марса. Между сферами Марса и Земли поместился додекаэдр; между Землей и Венерой – икосаэдр; между Венерой и Меркурием – октаэдр. Эврика! Великая тайна Вселенной была разрешена юным Кеплером, преподавателем протестантской школы в Граце.

Изумительно! [информирует Кеплер своих читателей] хотя у меня не было четкой идеи относительно порядка, в котором должны были быть расставлены совершенные тела, тем не менее, мне удалось (…) расположить их столь удачно, что впоследствии, когда я снова и снова проверял проблему, мне нечего было изменить. Теперь я уже не жалел о потерянном времени; работа уже не угнетала меня; я уже не боялся вычислений, пускай и очень сложных. День и ночь я проводил в расчетах, чтобы проверить, совпадают ли с коперниканскими орбитами предлагаемые мною, или всю мою радость унесет трезвым ветром (…) В течение нескольких дней все встало на место. Я видел как одно симметричное тело за другим столь точно вставляется между соответственными орбитами, что если бы крестьянин должен был спросить тебя, на каком виде крюка подвешены небеса, чтобы те не могли упасть, ты бы с легкостью ответил ему. Прощай! (из Mysterium Cosmographicum – Предисловие к читателю).

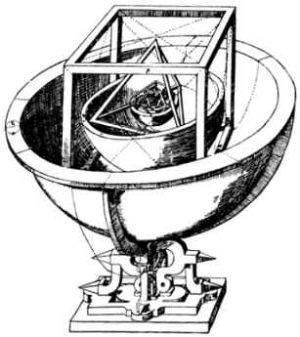
Модель вселенной; самая внешняя сфера принадлежит Сатурну.

Иллюстрация из книги Mysterium Cosmographicum Кеплера.

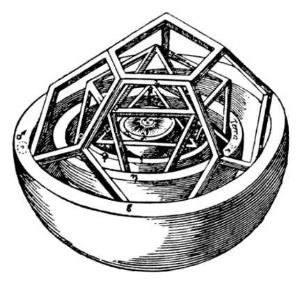
Деталь, представляющая сферы Марса, Земли, Венеры и Меркурия, с Солнцем в центре.

У нас имеется привилегия присутствовать при рождении одного из крайне редко документированных случаев фальшивой вдохновляющей идеи, мистификации высшего порядка от сократовского даймона, внутреннего голоса, который говорит с такой непоколебимой интуитивной уверенностью, обращаясь к обманутому разуму. Этот незабываемый момент перед чертежом на классной доске, несущим то же самое внутреннее убеждение как "Эврика!" Архимеда или же вспышка ньютоновского прозрения при виде падающего яблока. И все же, имеются несколько примеров, когда обман привел к моментальным и истинно научным открытиям, породившим Законы Природы. Вот чем привлекает нас Кеплер – и как личность, и как исторический пример. В случае Кеплера, ложная вера в пять совершенных тел не была преходящим наваждением, но осталась с ним, пускай и в измененной форме, до конца жизни, проявляя всевозможные симптомы параноидальной мании; тем не менее, она же подействовала в качестве vigor matrix (связующая энергия), побуждения к его бессмертным достижениям. Свою Misterium Cosmographicum Кеплер писал в возрасте двадцати пяти лет, но второе издание книги он опубликовал четверть века спустя, под самый конец, когда жизненные его труды были сделаны, когда сам он уже открыл свои три Закона, когда он разрушил Вселенную Птолемея и возвел фундаменты для современной космологии. Посвящение к этому второму изданию, написанное в возрасте пятидесяти лет, выдает живучесть его id?e fixe:

Почти что двадцать пять лет прошло с тех пор, как я опубликовал нынешнюю небольшую книжку (…) Хотя тогда я был совсем еще молодым, а это было публикацией моей первой работы по астрономии, тем не менее, ее успех в последующие годы громко заявил, что до сих пор никто и никогда не печатал более значимой, удачной и – учитывая ее содержание – стоящей первой книги. Было бы ошибкой рассматривать ее как чистое изобретение моего ума (любые мои предположения весьма далеко разошлись с моей целью, равно как и любые преувеличенные восхищение со стороны читателя, когда мы прикасаемся к семиструнной арфе мудрости Творца). Во всех отношениях, как будто бы некий небесный оракул продиктовал мне ее, напечатанная брошюра повсюду была признана превосходным и истинным прорывом (как и всегда случается при очевидном божественном вмешательстве).

Стиль Кеплера весьма часто бывает цветастым и помпезным, но крайне редко – до такой степени. Очевидной презумпция заключается в факте излучения этой его id?e fixe, эманации гигантского эмоционального заряда, который несут эти идеи. Когда пациент сумасшедшего дома заявляет, что он является глашатаем Святого Духа, для него это никак не хвастовство, а просто изложение факта.

И что же мы имеем здесь: молодого человека двадцати четырех лет, аспиранта теологии, с крайне обрывочными знаниями в области астрономии, охваченного безумной идеей, убежденного в том, что он разрешил-таки "космическую тайну". Если цитировать Сенеку, "нет крупных изобретений без примеси безумия", но, как правило, безумие пожирает изобретательность. История Кеплера покажет, как могут случиться исключения из этого правила.