7. Первый закон

Второй Закон определял изменения скорости планеты во время движения по орбите, но он не определял форму самой этой орбиты.

В конце Книги Второй, Кеплер заявил о неудаче своих попыток определить форму марсианской орбиты – неудаче, вызванной несоответствием в восемь дуговых минут. После этого он даже отправился далеким окольным путем, начиная с пересмотра движения Земли, после чего следовали физические размышления, что завершилось открытием Второго Закона. В Книге Четвертой Кеплер продолжает исследования марсианской орбиты с того места, в котором он остановился ранее. На сей раз, спустя четыре года после своих первых, неудачных подходов, он стал еще больше сомневаться в ортодоксальных догмах и добился несравнимого владения геометрией, изобретая свои собственные методики.

Окончательная попытка заняла почти два года; ее описание занимает с 41 по 60 главы Новой Астрономии. В первых четырех из них (41-44), Кеплер в последний раз, с дичайшей тщательностью, приписать Марсу круговую орбиту, и вновь переживает неудачу: этот раздел заканчивается такими словами:

А вывод здесь совершенно прост: пути планет не являются окружностями – они сворачивают вовнутрь с двух концов и наружу в противоположных концах. Такая кривая называется овалом. То есть, орбита представляет собой не окружность, но овальную фигуру.

Но вот тут случилась ужасающая вещь, и последующие шесть глав (45 – 60) представляют собой кошмарное путешествие через другой лабиринт. Для автора эта овальная орбита представляет собой дикие, пугающие дебри. Подкидывать все новые и новые круги и эпициклы, передразнивать рабских имитаторов Аристотеля – это дело одно, но вот приписывать совершенно новую, кривобокую, непредставимую тропу для небесных тел – это дело уже совершенно другое.

И действительно, ну почему овал? Ведь есть нечто в совершенной симметрии сфер и окружностей, обладающее глубинным, обнадеживающим обращением к подсознанию – в противном случае, это нечто не пережило бы целых два тысячелетия. Овал же не обладает всеми этими архетипными привлекательностями. И вообще, он обладает какой-то капризной формой. Он искажает ту вечную мечту о гармонии сфер, которая лежит в основе всего долгого пути. Кто ты таков, Иоганн Кеплер, чтобы порушить божественную симметрию? И все, что он способен сказать в свою защиту, это, что расчистив конюшню астрономию от кругов и спиралей, он оставил после себя всего лишь "тележку с навозом": свой овал (выражение из письма к Лонгомонтанусу 1605 г.).

К этому моменту интуиция лунатика изменила ему, может показаться, что он не мог преодолеть головокружения, потому хватается за первую же соломинку, которую может найти. А он обязан найти физическую причину, космическое raison d'?tre (разумное основание) для этого овала в небесах – и автор вновь обращается к старинному мошенническому средству, от которого он, вроде, уже отрекся: присобачиванию эпицикла! Правда, это чуточку другой эпицикл: у него имеется физическая причина. Ранее мы уже слышали о том, что когда сила Солнца "сметает" планеты, заставляя их двигаться по кругу, другая, антагонистическая сила, "располагающаяся в самой планете", заставляет ее вращаться по небольшому эпициклу в противоположном направлении. Такой оборот дела казался Кеплеру "удивительно подходящим", так что результатом совместного перемещения действительно является овал. Но овал очень даже особенный: он имеет форму яйца, с острым концом в перигелии и тупым концом в афелии.

Никто из философов до сих пор не откладывал столь чудовищных яиц. Или же, говоря словами самого Кеплера, произнесенными уже задним числом:

Случившееся со мной подтверждает старинную поговорку: в спешке сука рожает слепых щенков… Но я попросту не мог представить никаких иных средств для того, чтобы наставить планеты на овальную орбиту. Когда эта идея посетила меня, я уже праздновал свой новый триумф в отношении Марса, и мне в голову не приходил вопрос… а эти данные соответствуют истинным или нет… Таким вот образом я забрался в новый лабиринт… Читатель должен проявить терпимость к моей доверчивости (Новая Астрономия, том IV, глава 54).

Битва с яйцом продолжается целых шесть глав и занимает целый год жизни самого Кеплера. Это был трудный год; у автора не было денег, вновь вернулась "желчная лихорадка"; на небе появилась угрожающая новая звезда, nova 1604 года; фрау Барбара тоже была больна, а еще она родила сына – который дал возможность Кеплеру для одной из его несмешных и едких шуток: "В самое время, когда я был занят приведением в порядок своего овала, нежелательный гость проник в мой дом через тайный вход, чтобы отвлекать меня" (письмо к Д. Фабрициусу от 18 декабря 1604 г.).

Чтобы найти площадь своего яйца, Кеплер вновь рассчитал серию из ста восьмидесяти расстояний от Земли до Марса и сложил их вместе; и эту операцию он повторил не менее сорока раз. Чтобы заставить работать ничего не стоящую гипотезу, он временно отрекся от своего собственного, бессмертного Второго Закона – без какой-либо выгоды для себя. В конце концов, могло показаться, что его поразила некая снежная слепота: он держал решение в руке, но его не видел. 4 июля 1603 года он пишет приятелю, что не способен решить геометрические проблемы собственного яйца; но, "вот если бы формой был совершенный эллипс, все ответы можно было бы найти в работах Архимеда и Аполлония" (письмо к Д. Фабрициусу). Спустя восемнадцать месяцев Кеплер вновь пишет тому же корреспонденту, что истина должна лежать где-то посредине между яйцеобразной формой и окружностью, "как если бы орбита Марса была совершенным эллипсом. Но рассматривая это, я пока что ни до чего не дошел" (письмо к Д. Фабрициусу от 18 декабря 1604 г.). И что самое удивительное, Кеплер постоянно применял эллипсы в своих расчетах – но только лишь в качестве вспомогательного инструмента для определения, путем приближений, площади яйцеобразной кривой – что было истинным решением. Не стояли ли за всем этим некие бессознательные биологические отклонения? За исключением ассоциаций между приведением в порядок яйца и рождением ребенка, нет ничего такого, чтобы обосновало эту гипотезу[247].

Но, тем не менее, все эти годы блужданий в чащобе не были потрачены впустую. Другими словами, стерильные главы "Новой Астрономии", посвященные гипотезе яйца, представляют собой последующий и важный шаг к изобретению исчисления бесконечно малых. С другой стороны, мысли Кеплера сделались настолько насыщенными числовыми данными марсианской орбиты, что когда проявилась решающая опасность, разум ученого ответил незамедлительно, словно заряженная туча на искру.

А опасность эта, возможно, является самым невероятной случайностью во всей этой невероятной истории. Представилась она в виде числа, застрявшего в мыслях Кеплера. Числом этим было 0,00429.

Когда Кеплер наконец-то осознал то, что яйцо его "пошло с дымом" (Новая Астрономия, том IV, глава 55), и что Марс, который наш герой уже считал своим пленником, "безопасно закрепленным цепями к моим уравнениям, замурованным в моих таблицах", вновь вырвался на волю, Кеплер вновь решил начать все с самого начала.

Крайне тщательно он рассчитал ряд расстояний между Солнцем и Марсом в различных точках орбиты неуловимой планеты. Эти данные вновь показали то, что орбита представляла собой некий вид овала, выглядящей словно окружность, сплющенная с двух противоположных сторон, так что между окружностью и марсианской орбитой появлялись два узеньких серпа или "лунки". Величина серпа в самом широком его месте представляла собой 0,00429 от радиуса:

В этом самом месте, без какой-либо особенной причины, Кеплер заинтересовался величиной угла М – угла между Солнцем и центром орбиты, виденным с Марса. Этот угол назывался "оптическим уравнением". Понятное дело, он изменяется по мере перемещения Марса по орбите; максимальное его значение составляет 5? 18'. А теперь, узнаем, что случилось дальше, словами самого Кеплера (Новая Астрономия, том IV, глава 56):

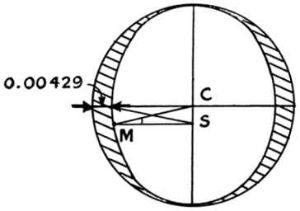
… Меня заинтересовало, почему и каким образом появился серп именно такой вот толщины (0.00429). В то время, как мысль эта кружила в моей голове, в то время, как я вновь и вновь понимал… что моя кажущаяся победа над Марсом была именно кажущейся, совершенно случайно, до меня дошло, что секанс (секанс угла М равен отношению MC:MS) угла 5? 18' является мерой самого крупного оптического уравнения. Когда я понял, что секанс этот равняется 1.00429, я почувствовал, будто бы пробудился ото сна…

Это было истинным лунатическим представлением. В первый момент, появление на свет числа 0,00429 могло показаться Кеплеру чудом. Но тут же у него мелькнуло в голове, что это кажущееся чудо должно быть порождено фиксированным отношением между углом при точке М и расстоянием до S, соотношение, которое должно быть верным для любой точки орбиты; только лишь способ, благодаря которому он наткнулся на это соотношение, был и вправду случайным. "Пути, ведущие людей к знаниям, столь же дивные, как само знание".

Наконец-то, после долгих ожиданий, через шесть лет невероятных трудов, Кеплер держал в руках тайну орбиты Марса. Сейчас он был способен выразить то, как меняется расстояние от планеты до Солнца с ее положением в различных точках пути, с помощью простой формулы, с помощью математического Закона Природы. Но до него так и не дошло, что эта формула, описывающая орбиту, представляет собой формулу для эллипса[248]. В настоящее время студент, обладающий даже малыми знаниями в аналитической геометрии, поймет это; но аналитическая геометрия появилась уже после Кеплера. Сам он открыл это волшебное уравнение эмпирически, вот только он никак не мог идентифицировать его как знак краткой записи эллипса, как и любой средний читатель данной книги; для самого Кеплера это уравнение было таким же бессмысленным. Кеплер достиг своей цели, но он не понял того, что цель уже достигнута.

Результатом стало еще одна, последняя, авантюра. Кеплер пытался сконструировать орбиту, которая бы соответствовала его новооткрытому уравнению; но он не знал, как это сделать, сделал ошибку в геометрии и получил кривую, которая была слишком выпученной, орбита была via buccosa, круглолицей, как он раздраженно отметил.

Что дальше? Мы добрались до кульминации комедии. В отчаянии Кеплер отбросил свою формулу (описывающую эллиптическую орбиту), поскольку желал испробовать совершенно новую гипотезу: испытать эллиптическую орбиту. Это было так же, как если бы турист после исследования меню сказал официанту: "А вот не хочу я вашу c?telette d'agneau, что бы это ни значило; принесите-ка мне котлету из ягненка".

Но на сей раз он уже был убежден в том, что орбита должна представлять собой эллипс, поскольку бесчисленные наблюдаемые положения Марса, которые он знал чуть ли не на память, неодолимо указывали на эту кривую; тем не менее, Кеплер так и не понял, что его уравнение, найденное им благодаря случайности плюс интуиции, и являлось уравнением эллипса. Потому-то он отбросил данное уравнение и сконструировал эллипс, воспользовавшись другим геометрическим методом. И только потом, лишь после того, до него дошло, что эти два метода дали один и тот же результат.

И со всей своей обычной, разоружающей честностью, он признался в случившемся:

Зачем мне умалять собственные слова? Истина Природы, которую я отбросил, и в погоню за которой бросился потом, вернулась незаметно, через заднюю крыльцо, надев иные одежды, чтобы ее приняли. Другими словами, я отложил [оригинальные уравнения] в сторону и возвратился к эллипсам, считая, что эта гипотеза достаточно отличная, в то время, как они оба (и уравнение, и эллипсы), как я докажу в следующей главе – это одно и тоже… Я размышлял и искал до тех пор, пока чуть не сошел с ума, причину, почему это планеты предпочитают эллиптические орбиты [моей орбите]… Ах, ну каким же глупышом я был! (Новая Астрономия, том IV, глава 58)

Но вот в Содержании, в котором он дает краткий конспект всей работы, Кеплер выражает проблему всего одним предложением:

Я показал [в этой главе], как бессознательно исправил свою ошибку.

Остальная часть книги представляет собой уборки, подчистки и подтирки после окончательной победы.