3. Первый приступ

Первое наступление Кеплера на проблему очень подробно описано в шестнадцатой главе Новой Астрономии.

Стоявшая перед ним задача заключалась в определении орбиты Марса посредством установления радиуса окружности, направления (по отношению к неподвижным звездам) оси, соединяющей две позиции, в которых Марс находится ближе всего и далее всего от солнца (перигелий и афелий), а так же положений Солнца (S), центра орбиты (С) и punctum equans (E), которые все лежат на этой оси. Птолемей предполагал, что расстояние между Е и С такое же, как и между С и S, но Кеплер подобных предположений не делал, что еще сильнее усложнило его задачу[241].

ПЕРИГЕЛИЙ

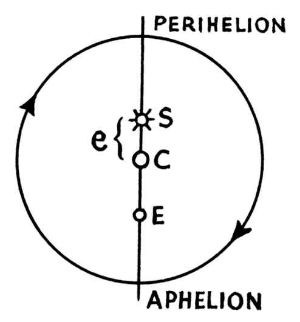
АФЕЛИЙ

Из сокровищницы Тихо Кеплер отобрал четыре наблюдаемых положения Марса в наиболее подходящие даты, когда планета находилась в оппозиции к Солнцу[242]. Геометрической проблемой, которую следовало разрешить, была, как мы видели, определение – из этих четырех позиций – радиус орбиты, направление оси и положение трех центральных точек на ней. Это была проблема, которую невозможно было решить посредством строгой математики, только путем аппроксимаций, то есть путем проб и ошибок, который следовало продолжать до тех пор, пока все кусочки головоломки не сойдутся с достаточным допуском. Невероятный объем потребовавшейся для этого работы можно оценить из того, что промежуточные расчеты Кеплера (сохранившиеся в рукописи) заняли девятьсот страниц in-folio, покрытых мелкими цифрами от руки.

Иногда Кеплер падал духом, он чувствовал, как Ретикус, что демон стучит его головой в потолок с воплями: "Вот каково движение Марса". Несколько раз он обращался за помощью к Маэстлину (который сделал вид, будто ничего не услышал), к итальянскому астроному Маджини (который поступил точно так же) и уже подумывал о том, чтобы послать сигнал SOS Франсуа Виету, отцу современной алгебры: "Приди, о галльский Аполлон, захватив свои цилиндры, сферы и любые другие геометрические принадлежности, что у тебя имеются…". Но в конце концов, ему пришлось над всем этим корпеть самому и изобретать по ходу дела свои собственные математические инструменты.

Где-то в средине этой драматической шестнадцатой главы его чувства прорываются наружу:

Если тебе [дорогой читатель] надоела эта изнурительная методика вычислений, пожалей хотя бы меня, которому пришлось проводить их, как минимум, семьдесят раз, затратив на это огромное количество времени; так что не удивляйся, что заканчивается уже пятый год, как я занялся Марсом…

И вот здесь, в самом начале этих ужасающих расчетов, Кеплер, не осознавая того, ввел три ошибочных величины для трех жизненно важных значений долготы Марса, но счастливо вывернулся с этим, так и не заметив собственной ошибки. Французский историк астрономии, Деламбр, впоследствии повторил все расчеты, но, к удивлению, его верные результаты очень мало отличаются от неверных результатов Кеплера. Причина этого заключается в том, что под конец главы Кеплер сделал ряд простых арифметических ошибок – ошибок в делении, за которые современный школьник обязательно получил бы двойку – но эти ошибки практически затушевали его ранние промахи. Вскоре мы сами увидим, что в наиболее важной точке процесса открытия своего Второго Закона Кеплер вновь совершил математические грехи, которые совместно аннулировались и "словно по мановению волшебной палочки" (по словам самого ученого) привели к верному результату.

В конце этой запирающей дух в груди главы Кеплеру кажется, будто бы он с триумфом достиг своей цели. В результате своих семидесяти с лишним попыток, он получил значения радиуса орбиты и для трех центральных точек, которые давали, с допустимой ошибкой менее чем 2', верные положения Марса для всех десяти оппозиций, задокументированных Тихо. Казалось, что непобедимый до сих пор Марс наконец-то побежден. Кеплер заявляет о своей победе весьма трезво:

Ты, усердный читатель, увидел теперь , что гипотеза, основанная на данной методе, не только удовлетворяет четыре позиции, на которых она сама основывалась, но и верно представляет, с точностью в две минуты, все остальные наблюдения…

После этого идут три страницы таблиц, доказывающих верность его претензий; а затем, без какого-либо перехода, следующая глава начинается такими вот словами:

И кто бы мог подумать, что такое возможно? Данная гипотеза, которая столь близко соответствует наблюдаемым оппозициям, оказалась, тем не менее, фальшивой…